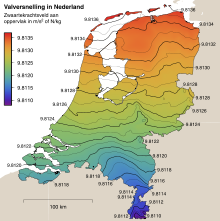
Valversnelling

De valversnelling, zwaarteveldsterkte en soms gravitatieveldsterkte, is de grootte en richting van het zwaartekrachtsveld. De valversnelling duidt men meestal aan met g en bedraagt op het oppervlak van de Aarde ongeveer 9,8 m/s².

Bij een grotere gewenste nauwkeurigheid vanaf twee cijfers achter de komma moet onderscheid worden gemaakt tussen twee varianten van het begrip valversnelling:

1. de versnelling corresponderend met de zwaartekracht zelf volgens de gravitatiewet van Newton
2. die waarbij de versnelling van maximaal 0,03 m/s² door de draaiing van de Aarde om zijn as vectorieel bij de zwaartekracht wordt opgeteld. Dit verkleint de grootte met maximaal 0,03 m/s² en ook de richting verandert meestal iets. Deze schijnbare versnelling, deze versnelling ten opzichte van het draaiende referentiekader van de Aarde wordt aan de middelpuntvliedende kracht toegeschreven.

Beide begrippen valversnelling zijn afhankelijk van de plaats op, boven of in de grond.

De verticale richting wordt meestal gedefinieerd als de richting van variant 2. Deze kan worden bepaald met een schietlood.

Gravimetrie bepaalt met behulp van een gravimeter, met een pendule-gravimeter, de grootte van variant 2. Indien gewenst kan het resultaat van deze metingen voor de verticale component worden gecorrigeerd om de grootte van variant 1 te bepalen.

Boven de grond of in bijvoorbeeld een schacht of grot is variant 2 ook de versnelling waarmee voorwerpen in vacuüm naar de aarde vallen in vrije val, dus als er geen andere krachten op werken dan de zwaartekracht, in een draaiend referentiekader.

Formule voor variant 1 bij bolsymmetrie

Bij benadering is de aarde bolsymmetrisch. De grootte van de eerste variant van de valversnelling op of boven de aarde wordt daarom bij benadering gegeven door:

$a=G\cdot {\frac {M}{r^{2}}}$

Met daarin:

$a$ de valversnelling in m/s²,

$G$ de gravitatieconstante oftewel 6,674 × 10⁻¹¹ m³ s⁻² kg⁻¹,

$M$ de massa van de aarde in kg,

$r$ de afstand tot het midden van de aarde in m.

De zwaartekracht van de Aarde wijkt hiervan af doordat de Aarde niet helemaal bolsymmetrisch is: de vorm wijkt af, en de massadichtheid op een bepaalde afstand van het middelpunt van de Aarde is niet helemaal onafhankelijk van de positie. Ook de breedtegraad en de hoogte van het terrein hebben invloed. Als voor de bekende gegevens wordt gecorrigeerd kunnen er anomalieën overblijven die nuttige informatie geven over de ondergrond. Omdat met een gravimeter na correctie de grootte van variant 1 wordt bepaald, wordt effectief alleen de verticale component van anomalieën bepaald.

Draaiend referentiekader

Variant 2 van de valversnelling in Nederland

Variant 2 van de valversnelling in België

Door de draaiing van de Aarde om zijn as heeft een voorwerp op of bij het aardoppervlak dat stilstaat ten opzichte van de Aarde een snelheid in oostelijke richting die varieert van nul aan de polen tot 465 m/s aan de evenaar. Op zichzelf veroorzaakt dit een schijnbare versnelling van de Aarde af, zonder zwaartekracht zou het voorwerp in een rechte lijn bewegen. Deze versnelling is recht evenredig met de afstand tot de omwentelingsas, die door de polen loopt, dus is op de evenaar het grootst, ongeveer 0,03 m/s², en op de polen gelijk aan nul. In het referentiekader van een stilstaande Aarde wordt in totaal een versnelling ervaren van de vectorsom van de gravitatieversnelling en de centrifugale versnelling, dus variant 2 van de valversnelling. Vermenigvuldigd met de massa geeft dit het ervaren (en door een weegschaal aangegeven) gewicht. Met de term verticaal wordt vaak de richting van variant 2 bedoeld, en met de term horizontaal de richtingen die daar loodrecht op staan. De totale versnelling in dit referentiekader bedraagt ongeveer 9,8 m/s². Als een met de Aarde meedraaiend voorwerp (dus een voorwerp dat in dit referentiekader stilstaat) wordt losgelaten en door een vacuüm valt krijgt het in dit referentiekader deze versnelling. Als er geen sprake is van een perfect vacuüm ondervindt het luchtweerstand.

Voorts is er, ook als gevolg van de rotatie van de aarde, een corioliskracht, die zorgt voor afbuiging als de val niet zuiver verticaal is. De corioliskracht staat altijd loodrecht op de snelheid en is recht evenredig met de grootte ervan. Dit effect is nauwkeurig aangetoond met de slinger van Foucault. Evenals de zwaartekracht is de corioliskracht evenredig met de massa.

Variant 1 op een bepaalde locatie kan zoals gezegd worden bepaald door van de gemeten variant 2 de centrifugale versnellingsvector af te trekken. Bij de meting met een weegschaal is een correctie voor de corioliskracht niet aan de orde.

Door de afplatting van de aarde is variant 1 net als de centrifugale versnellingsvector van de breedtegraad afhankelijk. Daarom worden bij het bepalen van anomalieën beide correcties vaak in één formule verwerkt, en wordt variant 1 dan dus niet apart uitgerekend. Anders gezegd, de gemeten waarden worden vergeleken met de normale valversnelling (normale grootte van variant 2 op zeeniveau) per breedtegraad.

Alle voorwerpen vallen in vacuüm even snel

Experiment met een vallende hamer en veer op de maan tijdens de Apollo 15 missie op de Maan.

De versnelling in vacuüm ten gevolge van zwaartekracht is voor alle voorwerpen gelijk. Giambattista Benedetti stelde dit in een gedachte-experiment en Jan Cornets de Groot en Simon Stevin voerden zo'n valproef daadwerkelijk uit vanaf de toren van de Nieuwe Kerk in Delft.

Als een voorwerp A bijvoorbeeld twee keer zo zwaar is als een voorwerp B dan is de gravitatiekracht op A eveneens tweemaal zo groot. Maar de massa van A — ofwel het "verzet tegen verandering van beweging" van A is ook twee keer zo groot. En volgens de tweede wet van Newton geldt $F=m\cdot a$ voor een constante massa. Dus als $F$ tweemaal zo groot is, en $m$ is ook tweemaal zo groot kan $a$ (= versnelling) hetzelfde zijn. Dit geldt ook als de kracht de zwaartekracht is en $a$ de valversnelling $g$.

Achtergrond is de gelijkheid van "zware massa" en de "trage massa": equivalentieprincipe, een van de basisprincipes van de algemene relativiteitstheorie, de gangbare theorie van de zwaartekracht.

Afwijkingen ten gevolge van de luchtweerstand

Een voorwerp dat door de lucht valt, ondervindt luchtweerstand, die niet afhankelijk is van de massa van het voorwerp, maar wel van de vorm, de afmetingen en de snelheid ten opzichte van de lucht. Een loden kogel en een plastic kogel van dezelfde afmetingen hebben bij een gegeven snelheid dezelfde luchtweerstand, maar ze vallen niet met dezelfde snelheid, omdat een kracht op een kleine massa een grotere vertraging veroorzaakt dan dezelfde kracht op een grote massa (conform de tweede wet van Newton).

Omdat de ondervonden luchtweerstand toeneemt met de snelheid, zal een voorwerp dat lang genoeg valt, een constante eindsnelheid bereiken en geen verdere versnelling meer ondergaan. Dit is voor parachutisten een bekend ervaringsfeit.

De val van een object van eindige afmetingen door de lucht wordt beheerst door de Wet van Stokes.

Groottes van de valversnelling

Valversnelling uitgedrukt in g op toenemende hoogte in km

De grootte van de valversnelling bedraagt op het oppervlak:

Plaats	Variant 2 van de valversnelling (m/s²)
Evenaar	9,780
Keerkringen	9,788
Benelux	9,813
Pool	9,832

Aan de evenaar is variant 2 van de valversnelling dus 0,052 m/s² minder dan aan de polen. Hiervan is 0,033 m/s² er het gevolg van dat de Aarde om zijn as draait. Aan de evenaar is variant 1 van de valversnelling dus 0,019 m/s² minder dan aan de polen. Dit is het gevolg van de afplatting van de Aarde.

De waarde van de valversnelling neemt kwadratisch af met de afstand tot het middelpunt van het hemellichaam; in ons geval de Aarde in ons geval. De standaardvalversnelling, gebruikt voor bijvoorbeeld de definitie van kilogramkracht, is 9,80665 m/s². Voor de Maan is de valversnelling 1,62 m/s².

Websites

• UIUC. How Gravitational Force Varies at Different Locations on Earth. blog