Summen von Vektorräumen
(321) Summen von Teilräumen
Sind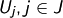 (Indexmenge) Teilräume eines
(Indexmenge) Teilräume eines  -Vektorraumes
-Vektorraumes 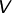 , so
heißt der von der Vereinigung
, so
heißt der von der Vereinigung  erzeugte Teilraum
von V die Summe der
erzeugte Teilraum
von V die Summe der 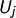 . Wir schreiben
. Wir schreiben
Sind
Mit Hilfe des Satzes folgt:
Speziell: Sind  ,
,  Teilräume von
Teilräume von 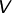 , so ist
, so ist
Satz.
Seien  ,
,  Teilräume eines
Teilräume eines  -Vektorraumes
-Vektorraumes 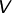 , und sei
, und sei  . Dann sind folgende Bedingungen äquivalent:
. Dann sind folgende Bedingungen äquivalent:
- Ist
 für
für 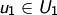 ,
, 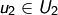 , dann ist
, dann ist

- Für jedes
 ist die Darstellung
ist die Darstellung  eindeutig
eindeutig
-

Beweis.
 Seien
Seien  mit
mit 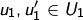 ,
,  zwei Darstellungen von
zwei Darstellungen von  . Zu zeigen:
. Zu zeigen:  und
und  . Da
. Da

 Sei
Sei 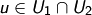 . Zu zeigen:
. Zu zeigen: 
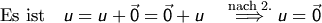
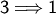 Sei
Sei  . Zu zeigen
. Zu zeigen 

Definition.
- Seien
 ,
,  Teilräume eines
Teilräume eines  -Vektorraumes. Dann heißt
die
Summe
-Vektorraumes. Dann heißt
die
Summe  die (innere) direkte Summe
von
die (innere) direkte Summe
von  und
und  ,
falls eine der Bedingungen (und damit alle) aus obigem Satz
erfüllt sind. Wir
schreiben dann:
,
falls eine der Bedingungen (und damit alle) aus obigem Satz
erfüllt sind. Wir
schreiben dann:

- Seien
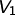 ,
, 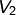 beliebige
beliebige  -Vektorräume. Wir definieren die
(äußere) direkte Summe als
-Vektorräume. Wir definieren die
(äußere) direkte Summe als

mit komponentenweiser Addition und Skalarmultiplikation.
Beispiel.
Sei  und
und  und
und  . Dann
ist
. Dann
ist 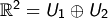 die innere direkte Summe, da
die innere direkte Summe, da  .
.
Sei und
und  . Dann ist
. Dann ist 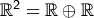 die
äußere
direkte Summe. Analog ist
die
äußere
direkte Summe. Analog ist  eine äußere direkte Summe.
eine äußere direkte Summe.
Sei