Erzeugendensysteme
Sei 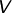 ein
ein  -Vektorraum und
-Vektorraum und 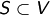 . Ist
. Ist 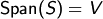 , so heißt
, so heißt
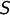 ein Erzeugendensystem von
ein Erzeugendensystem von 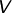 .
.
Ist also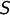 ein Erzeugendensystem, dann gibt es zu jedem
ein Erzeugendensystem, dann gibt es zu jedem  ein
ein  sowie Elemente
sowie Elemente  ,
, 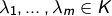 , mit
, mit 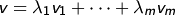 Wenn
Wenn 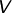 eine endliche Teilmenge
eine endliche Teilmenge
 als
Erzeugendensystem besitzt, so heißt
als
Erzeugendensystem besitzt, so heißt 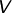 endlich
erzeugt. Es ist dann
endlich
erzeugt. Es ist dann
Ist also
Zum Beispiel
Beispiel.
Seien  ,
,  und
und  . Dann sind
. Dann sind  und
und  Teilräume von
Teilräume von 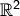 , aber
, aber  ist kein
Vektorraum, denn
ist kein
Vektorraum, denn 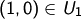 ,
,  aber
aber  .
Der von
.
Der von  aufgespannte Teilraum von
aufgespannte Teilraum von 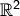 ist die Summe
ist die Summe

Hier gilt zusätzlich noch .
.
Hier gilt zusätzlich noch
Beispiel.
Sei  mit
mit  , dann bilden
, dann bilden 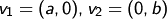 und
und  ein Erzeugendensystem von
ein Erzeugendensystem von 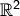 .
.

 entbehrlich ist.
entbehrlich ist.
Beweis.
Sei 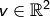 beliebig. Dann ist
beliebig. Dann ist 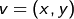 mit
mit  . Es
folgt
. Es
folgt

mit 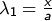 ,
,  und
und 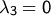 .
.
Man sieht insbesondere, dass Beispiel. Bilden 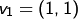 ,
,  ein Erzeugendensystem von
ein Erzeugendensystem von
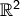 ?
?
Ansatz:
Ansatz:

also

Die Vektoren  und
und 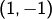 bilden also ein Erzeugendensystem, da
bilden also ein Erzeugendensystem, da
mit 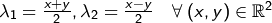 gilt.
gilt.
Beispiel. Bilden 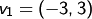 ,
,  ein Erzeugendensystem
von
ein Erzeugendensystem
von 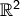 ?
?
Ansatz:
Ansatz:
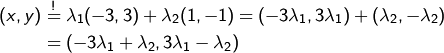
also
Dieses Gleichungssystem ist aber nicht für alle  lösbar,
denn setze z.B.
lösbar,
denn setze z.B.  , dann ist das System
, dann ist das System
nicht lösbar. Insbesondere ist 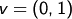 keine Linearkombination von
keine Linearkombination von
 und
und  .
.