허프 변환
허프 변환(Hough transform)은 디지털 화상 처리, 컴퓨터 비전 등에서 사용하는 용어이다.
개요
[편집]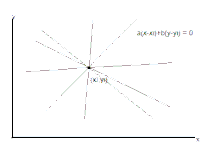
한 평면 위에 놓여 있는 점들의 집합 P에서 원소 (xi, yi)를 지나는 모든 직선을 그림 1과 같이 표시할 수 있다.
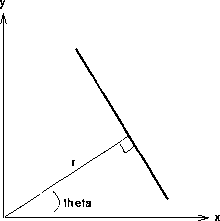
- [식 1]
즉, 어떠한 점을 지나는 직선은 위의식 xcosθ + ysinθ = r 로 표시될 수 있다. 위의 [그림2]그래프와 [식 1]을 보면 x와 y는 변수, θ와 r은 상수임을 알 수 있다. (기본적으로 θ 의 범위는 [0,π]이다. 그래야만 직선이 unique하기 때문이다.)
지금 이 파트에서의 관심에 대해 주의깊게 생각해야 한다. 이 파트의 관심 사항은 점들이 놓여있는 평면에서 어떤 직선 위에 있는 점들의 개수를 파악 할 수 있는지가 핵심이다. Hough는 이 문제를 아래와 같이 생각했다. [그림 1]과 같이 어떤 점을 지나가는 무수히 많은 직선들이 존재한다. 그러면 [식 1]에서 이것을 표현해 보면 어떻게 될까?
- 지금까지 변수로 생각했던 x,y는 상수가된다. 왜냐?
- 직선은 이 점을 무조건 지나가야 하기 때문에, 지금까지 상수로 생각했던 theta와 r은 변수가 된다. 왜냐?
- [식 1]은 직선 한 개에 해당하는 식이다. 하지만 지금은, 고정된 x와y를 지나는 무수히 많은 직선들을 표현해야 한다.
- 그렇기 때문에 theta 와 r은 변수가 되어 수많은 직선을 만들어야 한다.
즉, 어떤 점(x,y)를 지나는 무수히 많은 직선을 [식 1]을 가지고 표현 할 수 있다. 당연히 축은 theta와 r이 된다. 변수니까. 그리고 식은 sin곡선과 같은 곡선을 그릴 것이다. 예를 들어 그 곡선이 아래 그림과 같은 것이라고 가정해 보자.

위에서[그림 3] 보는 곡선 a는 (x0,y0)를 지나는 모든 선들을 표현한다. 지금까지는 점 한개를 고려하면서 생각해보았는데 좀 더 확장해보자. 여러 개의 점이 있을 경우 각각의 점은 [그림 3]와 같은 r,theta평면 상에서 곡선들을 갖게 될 것이다.
(x0,y0)를 지나는 모든 선들이 r,theta평면에서 하나의 곡선으로.. (x1,y1)를 지나는 모든 선들이 r,theta평면에서 또 하나의 곡선으로.. (x2,y2)를 지나는 모든 선들이 r,theta평면에서 또 하나의 곡선으로.. ... (xi,yi)를 지나는 모든 선들이 r,theta평면에서 또 하나의 곡선으로.. ...
이런식으로 생각 할 수 있다. 그러면 여기서 하나의 질문이 생긴다. 이 r,theta평면에서 곡선들이 있는데, 이 곡선들의 교점은 무엇을 의미하나?? 교점이라 함은 어떤 곡선과 어떤 곡선이 공통된 값이 존재한다는 것이다. 예를 들어 보자. 곡선 a1 과 곡선 a2가 있다고 가정하자.
a1: x1*cosθ + y1*sinθ = r a2: x2*cosθ + y2*sinθ = r
이 두 곡선이 교점이 생겼다라는 것은 (x1,y1)을 지나는 직선들중 하나의 직선과 (x2,y2)을 지나는 직선들중 하나의 직선이 같아졌다는 것을 뜻한다. 즉 점(x1,y1)과 점(x2,y2) 은 하나의 같은 점 선 위에 있다는 것이다. 그러면 만약 곡선 3개가 한점에서 만났다 라는 것은 점 3개가 하나의 직선위에 있다 라는 것을 뜻한다. 한마디로 말하자면, n개의 곡선이 한점에서 만나면 n개의 점이 하나의 직선위에 있다 라는 것을 뜻한다.
즉, 해당 교점의 좌표(r,theta평면위의)를 가지고 (xy평면에)직선을 그리면 n개의 점을 가지고 있는 직선을 그릴 수 있는 것이다. 위와 같은 과정을 통해 우리는 어떤 선 위에 점이 몇 개 올라와 있는지 그 개수를 파악할 수 있게 되었다.
코딩할 때에는 이미지가 디지털 같이 정수로 딱딱 끊어지기 때문에 어떤 픽셀에서 몇 번 겹쳐지는가에 대해서 파악하기 쉽다.
같이 보기
[편집]참고 문헌
[편집]- Richard O. Duda and Pete E. Hart Stanford Research Institute, Menlo Park, California Use of the Hough Transformation To Detect Lines and Curves in Pictrues
- https://homepages.inf.ed.ac.uk/rbf/HIPR2/hough.htm

