Stati di Bell
Gli stati di Bell sono un concetto di Informatica quantistica. Sono stati quantici di due qubit che rappresentano gli esempi più semplici (e massimali) di correlazione quantistica chiamato anche entanglement quantistico. Gli stati di Bell sono una base di vettori correlati e normalizzati. La normalizzazione implica che la probabilità complessiva della particella di essere in uno degli stati menzionati è 1. La correlazione è un risultato indipendente dalla base del principio di sovrapposizione. Un principio secondo cui una particella si trova in più stati contemporaneamente. A causa di questa sovrapposizione, la misurazione del qubit lo farà collassare in uno dei suoi stati base con una data probabilità. A causa della correlazione, la misurazione di un qubit assegnerà all'istante uno dei due possibili valori all'altro qubit, dove il valore assegnato dipende da quale stato Bell i due qubit sono. Gli stati Bell possono essere generalizzati per rappresentare specifici stati quantistici di sistemi con molti qubit, come lo stato GHZ per 3 sottosistemi.
La comprensione degli stati di Bell è essenziale nell'analisi della comunicazione quantistica (come la codifica superdensa, o superdense coding) e il teletrasporto quantistico. Il teorema di non-comunicazione implica che due osservatori macroscopici non possano sfruttare il teletrasporto quantistico per trasmettere informazioni più velocemente della velocità della luce, poiché è necessario che A comunichi le informazioni a B.
Stati di Bell
[modifica | modifica wikitesto]Gli stati Bell sono quattro specifici stati quantistici di due qubit con la massima correlazione. Sono in una sovrapposizione di 0 e 1 cioè una combinazione lineare dei due stati. La loro correlazione significa quanto segue:
Il qubit posseduto da Alice (pedice "A") può essere 0 e 1. Se Alice misurasse il suo qubit in una base standard, il risultato sarebbe perfettamente casuale, 0 o 1 entrambi con probabilità 1/2. Ma se Bob (pedice "B") misurasse il suo qubit, il risultato sarebbe lo stesso di quello ottenuto da Alice. Quindi, se Bob misurasse il suo qubit, otterrebbe un risultato casuale a prima vista, ma se Alice e Bob comunicano, scoprirebbero che sebbene i loro risultati sembrino casuali, sono perfettamente correlati.
Questa perfetta correlazione a distanza è speciale: forse le due particelle hanno concordato in anticipo, quando la coppia fu creata (prima che i qubit venissero separati), quale risultato mostrare in caso di una misurazione.
Quindi, seguendo Einstein, Podolsky e Rosen nel 1935 nel loro famoso EPR paper, c'è qualcosa che manca nella descrizione della coppia di qubit di cui sopra, vale a dire questo accordo, chiamato più formalmente una variabile nascosta.
Base di Bell
[modifica | modifica wikitesto]Nel suo famoso articolo del 1964, John S. Bell mostrò con semplici argomenti della teoria della probabilità che queste correlazioni (quella per la base di 0,1 e quella per la base di +, -) non possono essere rese entrambe perfette dall'uso di un pre-accordo memorizzato in alcune variabili nascoste; ma che la meccanica quantistica predice le correlazioni perfette. In una formulazione più formale e raffinata nota come disuguaglianza Bell-CHSH, mostra che una certa misura di correlazione non può superare il valore 2 se si assume che la fisica rispetti i vincoli della teoria locale della variabile nascosta (una sorta di formulazione di senso comune di come viene trasmessa l'informazione), ma certi sistemi consentiti nella meccanica quantistica possono raggiungere valori alti come . Pertanto, la teoria quantistica viola la disuguaglianza di Bell e l'idea di variabili nascoste locali.
Quattro stati specifici a due qubit con il valore massimo di sono designati come stati Bell. Sono conosciuti come i quattro stati a correlazione massima di due qubit e formano una base a massima correlazione nota come base di Bell, dello spazio di Hilbert quadridimensionale per due qubit:
- (1)
- (2)
- (3)
- (4)
Creare stati di Bell
[modifica | modifica wikitesto]Sebbene ci siano molti modi possibili per creare stati correlati di Bell attraverso circuiti quantistici, il più semplice usa una base di calcolo come input e contiene una porta di Hadamard e una porta CNOT (vedi la figura seguente). Come nell'esempio, le immagini del circuito quantistico accettano i due input qubit e li trasformano nel primo stato Bell. Esplicitamente, la porta di Hadamard trasforma in una sovrapposizione di . Questo sarà l'ingresso di controllo alla porta CNOT, che inverte l'output solo quando il controllo è 1. Quindi, la porta CNOT trasforma il secondo qubit come segue .
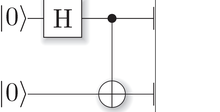
Per i quattro ingressi di base a due qubit, , il circuito emette uno stato Bell finale secondo l'equazione
dove è la negazione di .[1]
Dopo aver misurato il primo qubit, si ottengono due risultati possibili per il secondo qubit, 0 con ½ probabilità e 1 con ½ probabilità. Ciò implica che i risultati della misurazione sono correlati. John Bell fu il primo a dimostrare che le correlazioni di misura nello stato di Bell sono più forti di quanto potrebbero mai essere tra sistemi classici. Questo suggerisce che la meccanica quantistica consente l'elaborazione delle informazioni al di là di ciò che è possibile nel mondo classico. Inoltre, gli stati di Bell formano una base ortonormale e possono quindi essere definiti con una misurazione appropriata. Poiché gli stati di Bell sono stati correlati, le informazioni sull'intero sistema possono essere note, mentre si nascondono le informazioni sui singoli sottosistemi. Ad esempio, lo stato Bell è uno stato puro, ma l'operatore a densità ridotta del primo qubit è uno stato misto. Lo stato misto implica che non tutte le informazioni su questo primo qubit sono note.[1] Gli stati di Bell sono simmetrici o antisimmetrici rispetto ai sottosistemi.
Note
[modifica | modifica wikitesto]- ^ a b Michael A. Nielsen e Isaac Chuang, Quantum Computation and Quantum Information, Cambridge University Press, 2010, ISBN 9781139495486.












