Pressoflessione
La pressoflessione è una sollecitazione composta da compressione e flessione, ovvero generata da una forza assiale di compressione e da un momento flettente.
Pressoflessione semplice e deviata
[modifica | modifica wikitesto]La pressoflessione semplice è una sollecitazione generata da uno sforzo normale associato ad un momento flettente. La pressoflessione deviata è una sollecitazione generata da uno sforzo normale, associato ad una flessione deviata, cioè derivante dalla somma di due componenti (momenti flettenti , ).
La pressoflessione può essere anche generata da uno sforzo normale eccentrico come nel tipico caso di un pilastro con carico non assiale.
Resistenza a pressoflessione
[modifica | modifica wikitesto]Occorre sottolineare che vi sono materiali resistenti a trazione, acciaio, calcestruzzo armato in modo idoneo, e viceversa materiali che resistono poco o nulla, come il terreno. In quest'ultimo caso è sempre bene avere il centro di pressione all'interno del nocciolo centrale di inerzia.
Nel caso di pressoflessione semplice e materiale resistente a trazione, adottando le ipotesi di D.S.V. (mantenimento delle sezioni piane...) è possibile calcolare la tensione che sollecita una generica fibra della sezione, a distanza y dall'asse x, utilizzando il P. S. E., sommando cioè le singole tensioni derivanti dalle singole C.D.S.:
- tensione di una generica fibra della sezione (convenzionalmente positiva se di trazione, negativa se di compressione)
- sforzo normale
- area della sezione
- momento flettente
- modulo di resistenza
- momento di inerzia della sezione in esame
- y distanza della generica fibra dall'asse x
Osservando la formula, oppure ragionando ad intuito con le grandezze coinvolte, si può notare che:
- un momento di inerzia elevato, essendo a denominatore, consente una riduzione della tensione sollecitante.
- Il momento flettente sollecitante elevato innalza la tensione sollecitante.
- La tensione ha un andamento lineare che ricade nella compressione (o trazione semplice) se il momento è nullo; flessione semplice se lo sforzo normale è nullo.
Pressoflessione e relazioni tra asse neutro e nocciolo centrale d'inerzia in materiali reagenti a trazione
[modifica | modifica wikitesto]Quando un solido trave (generalmente prisma a sezione rettangolare) è soggetto a sforzo normale eccentrico, il punto in cui è applicato lo sforzo normale (centro di pressione) ha retta d'azione parallela ma non coincidente con l'asse baricentrico della trave. Il centro di pressione è cioè spostato rispetto al baricentro della sezione dei valori che determinano l'eccentricità. Ad esempio nel caso più semplice di sforzo normale e flessione retta attorno all'asse x, risulta . Affrontando invece il caso più generale di sforzo normale associato a flessione deviata, ci proponiamo di calcolare l'equazione dell'asse neutro; dette xc e yc le coordinate di applicazione della forza N, i momenti di tale forza rispetto agli assi x e y risultano essere: . La tensione che si creerà sulla sezione sarà data da: Spesso l'equazione dell'asse neutro viene fornita in funzione del giratore di inerzia L'asse neutro n sarà quello per cui:
A piccoli valori dell ' eccentricità corrisponde una maggiore distanza dell'asse neutro dal baricentro. L'asse neutro risulta l'antipolare del centro di sollecitazione C. È lecito asserire che l'asse neutro è secante, tangente o esterno alla sezione a seconda che C sia disposto all'esterno, sul contorno o nell'interno del nocciolo centrale di inerzia. Nel 1º caso l'asse neutro taglia la sezione quindi questa risulta essere parte tesa e parte compressa. Nel 2º caso l'asse neutro è tangente alla sezione: le tensioni hanno stesso segno e si annullano nel punto di contatto. Nel 3º caso l'asse neutro è esterno alla sezione e le tensioni hanno ovunque lo stesso segno e non si annullano in nessun punto della sezione. Il disegno del nocciolo centrale di inerzia (figura piana con centro nel baricentro della sezione) si esegue per via analitica o grafica se si conosce l'ellisse centrale e se si seguono le proprietà di antipolarità di inerzia: se la figura presenta un vertice, ad esso corrisponde un tratto rettilineo del nocciolo e, viceversa, se la figura presenta un tratto rettilineo, ad esso corrisponde un vertice del nocciolo. Si deduce quindi che il nocciolo è sempre una figura convessa. Se la sezione è poligonale, anche il nocciolo è poligonale. Se la sezione e circolare anche il nocciolo sarà circolare. I raggi di nocciolo sono dati da:
Dalla definizione di giratore segue:
Per esempio in una sezione quadrata il raggio di nocciolo vale:
Calcolo tensioni in materiali non resistenti a trazione
[modifica | modifica wikitesto]Prendendo in considerazione una qualunque sezione rettangolare di dimensioni , omogenea e sottoposta a pressoflessione, analizziamo tre casi, a seconda del punto di applicazione della forza di compressione, quindi della sua eccentricità. Il materiale ipotizzato ha una resistenza a trazione bassa (terreno, muratura, mattoni, pietre naturali, etc..); poiché la rottura in questa tipologia di materiali è di tipo fragile, è preferibile non affidarsi alle loro capacità di resistere a trazione, introducendo l'ipotesi cautelativa che essi non resistono per nulla a sforzi di trazione. È chiaro che la situazione ideale sarebbe ottenere l'intera sezione compressa (centro di pressione contenuto dentro il nocciolo centrale di inerzia); se il centro di pressione si trova al di fuori del nocciolo ma ancora all'interno della sezione, l'equilibrio è ancora possibile ma deve essere garantito solo da tensioni di compressione. Di conseguenza la posizione dell'asse neutro non coincide con quella che avrebbe assunto nel caso in cui il materiale fosse stato in grado di sviluppare anche tensioni di trazione. La zona compressa ha estensione minore e nella rimanente parte di sezione si produrrà un lieve distacco tra una faccia e l'altra. L'equilibrio è invece impossibile se il centro di pressione cade al di fuori della sezione perché dovrebbe essere garantito da sole tensioni di trazione che il materiale non è, per ipotesi, in grado di sviluppare.
- Calcolo eccentricità
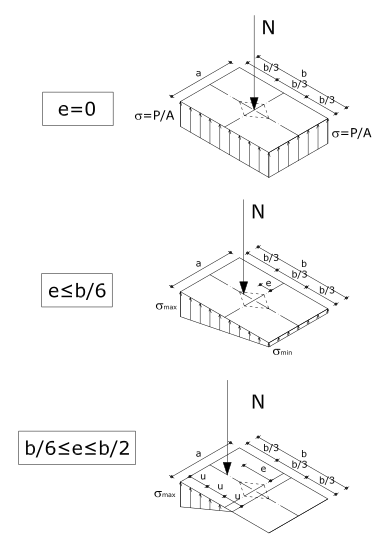
- Eccentricità nulla (compressione pura)
- Piccola eccentricità (compressione e flessione retta)
In piccola eccentricità valgono le ipotesi di D.S.V. Le sezioni si mantengono piane, ed è possibile applicare il principio di sovrapposizione degli effetti. Ecco allora che la tensione sulla sezione rettangolare soggetta a pressoflessione può essere calcolata come la somma della tensione dovuta a sforzo normale centrato con quella dovuta a flessione retta (Navier).
per sezione rettangolare segue che:
- Grande eccentricità (materiali non resistenti a trazione) cioè
L'eccentricità risulta maggiore del raggio di nocciolo. Il centro di pressione non può fuoriuscire dalla sezione, altrimenti non ci sarebbe più equilibrio.
Posso calcolare la distanza tra il centro di pressione e il bordo più sollecitato a compressione:
Non conosco a priori quanto vale l'area reagente, tantomeno la posizione dell'asse di separazione (l'asse neutro nel caso di materiali non resistenti a trazione); mi viene in aiuto però la geometria della sezione. Infatti io so che il diametro principale del nocciolo di una sezione rettangolare è pari ad 1/3 del lato al quale è parallelo. Allora questa area reagente è lunga . Poiché le tensioni si annullano sull'asse di separazione, allora il centro di pressione C deve stare per forza sul bordo del nuovo nocciolo relativo all'area reagente, posizione in cui si sviluppa la . Quindi la distanza dell'asse di separazione dal bordo più compresso sarà .
In condizioni di equilibrio lo sforzo normale di compressione deve eguagliare la reazione dell'area resistente:
ma
eguagliando le forze segue che:
Esempio
[modifica | modifica wikitesto]Una gru, installata in un cantiere edile, solleva all'estremità del suo braccio un carico di 500 kgf (kilogrammi-forza). La fune a cui è appeso il carico, soggetta a trazione, provoca una flessione nel braccio a cui la fune è appesa. Il braccio trasferisce la sollecitazione sotto forma di pressoflessione nella torre (traliccio verticale che può ruotare attorno al proprio asse nel caso di gru con rotazione alla base, oppure rimane fisso nel caso di gru con rotazione alta, dove ruota solo il braccio).
- il contrappeso serve a controbilanciare il momento meccanico del peso.
- il materiale che costituisce il traliccio strutturale deve possedere adeguata resistenza meccanica, sia a trazione che a compressione.
- il plinto che sorregge la torre ha dimensioni ampie, 5m x 5m o più (solitamente), poiché il terreno non resiste a trazione ed in caso di dimensionamento mal progettato, si può verificare una eccessiva parzializzazione della sezione resistente della fondazione. Il traliccio deve anche essere ben collegato ad essa, per evitare pericolose rotture.
- Se il carico è in punta, il limite massimo del carico sollevabile sarà inferiore rispetto al limite massimo corrispondente ad un posizionamento a metà del braccio o vicino alla torre della gru.
Approfondimenti
[modifica | modifica wikitesto]La trattazione della pressoflessione è studiata mediante l'ausilio della geometria delle masse ed in particolare con l'uso del nòcciolo centrale d'inerzia.