לוגיקה
ערך ללא מקורות
| ||
| ערך ללא מקורות | |
לוֹגִיקָה (מיוונית: λογική; בעברית: תּוֹרַת הַהִגָּיוֹן) היא שם כולל לתורות הבוחנות קשרי היסק בין טענות תוך התבססות על אקסיומות.
הלוגיקה מנתחת צורה של טענות, ועל סמך ניתוח זה מציעה כללים שבעזרתם ניתן לקשר טענות זו לזו ומכאן להסיק מסקנות. הלוגיקה מבחינה בין טיעונים שיש בהם היסק תקף, כלומר כאלה שבהם המעבר מההנחות למסקנה הוא מוצדק, לבין טיעונים שאינם תקפים. לפיכך הלוגיקה היא בראש ובראשונה תורה המתארת את אופני החשיבה שהם תקפים באופן אובייקטיבי כביכול ואת אופני ביטוייהם.
במאה ה-19 וה-20 חווה ענף הלוגיקה התפתחות משמעותית עקב התמקדות המחקר באופן בו ניתן לזקק מבנה לוגי באמצעות שפות מלאכותיות המושתתות על אופני ביטוי סימבוליים, ללא תלות בתחביר של השפה הטבעית. כך נולדה הלוגיקה המתמטית, המתמקדת במושג ההוכחה ובתכונותיהן של מערכות אקסיומטיות שונות. לפיכך בעוד שבראשית הלוגיקה נושא המחקר היה חוקי החשיבה המדויקת, נכון יותר לתאר את העניין של הלוגיקה המודרנית כעיסוק בתכונותיהן הצורניות של קבוצות של טענות באשר הן.
מקורו של המונח לוגיקה מהמילה היוונית לוגוס (λόγος), שלה פירושים שונים כגון 'סיבה', 'מחשבה', ו'טיעון'. התרגום העברי המסורתי ל'לוגיקה' הוא 'תורת ההיגיון'.
התורה הלוגית הנפוצה ביותר בעולם המדע היא לוגיקה פורמלית וגרסתה המקובלת כיום היא זו המתבססת על תורת הקבוצות האקסיומטית. תורות מתמטיות רבות נשענות על גרסה זו של הלוגיקה הפורמלית המעניקה להן בסיס לוגי-דדוקטיבי.
תולדות הלוגיקה
[עריכת קוד מקור | עריכה]מראשיתה ועד תקופת אפלטון
[עריכת קוד מקור | עריכה]ראשיתה של הלוגיקה במחקר הפילוסופי אודות תכונותיהם של טיעונים. מחקר זה התפתח במיוחד ביוון העתיקה, ובעיקר במסגרת האסכולה האלאטית. פרמנידס ותלמידו זנון התמחו בניסוחם של טיעונים פרדוקסליים, המראים כי ישנן סתירות במושגים באמצעותם אנו מבינים את המציאות, במיוחד בכל הנוגע למושגים רצף ואינסוף. את הסתירות הללו ניתן לחשוף באמצעות הצגת הקשרים בין המושגים השונים שלנו בצורה של טיעון, שעל אף שאנו נוטים לקבל את הנחותיו, מסקנתו בלתי נסבלת (למשל, שאין שינוי בעולם, שאין בו תנועה וכולי). הסיבה לכך שסתירות אלו עולות, היא שהבנתנו הראשונית את המושגים הנוגעים לעולם החושים אינה מתוחכמת מספיק; בעקבות הסתירות, אנו נאלצים לחשוב מחדש על האופן בו עלינו להבין אותם.
אפלטון יכול להחשב כממשיך דרכם של האלאטים. אפלטון אמנם לא הציג תורה לוגית סדורה, אולם בדיאלוגים המיוחסים לו הוא חקר מספר מושגים לוגיים יסודיים, למשל את ההבחנה בין טיעונים שבמבנה שלהם קיימת סתירה פנימית, לבין טיעונים שהתוכן שלהם עקבי, כלומר שאין בו סתירות פנימיות. לשם כך ביקש אפלטון להבהיר את מושג ההגדרה (יוונית: Horismos), שכן ללא הגדרות חדות של המושגים אודותם נסובים טיעונינו, קשה להבחין מתי אנו סותרים את עצמנו. בדיאלוג האפלטוני הטיפוסי, סוקרטס בוחן נושא מסוים (למשל, מהו אומץ או מהי ידידות) ושואל את שאר המשתתפים בדיאלוג שאלות כדי לבדוק עד כמה הם עקביים בדעותיהם על נושא זה. לעיתים ניתן לחלץ מן הדיאלוג מערכת של משפטים, המרכיבים יחדיו טיעון, ולנתח את הדיאלוג כחקירה המכוונת לבדוק האם כל המשפטים עקביים עם עצמם ועם המשפטים האחרים בהם מאמינים המשתתפים בדיאלוג. למתודה זו של בירור לוגי קרא אפלטון דיאלקטיקה.
עיקרון לוגי יסודי שאפלטון זיהה לראשונה הוא חוק הסתירה, על פיו אין דבר יכול לשאת תכונות מנוגדות זו לזו:
"ברור שאותו הדבר עצמו לא יעשה או יסבול בעת ובעונה אחת דבר והיפוכו, על כל פנים לא מאותה בחינה עצמה ולגבי אותו העניין עצמו; ולפיכך, אם נמצא שכך יארע בהללו, נדע שאינם אותו הדבר עצמו, אלא מרובים" (פוליטיאה, 436ב).
לוגיקה אריסטוטלית
[עריכת קוד מקור | עריכה] ערך מורחב – הלוגיקה של אריסטו
ערך מורחב – הלוגיקה של אריסטו
גישתו של אריסטו ללוגיקה הייתה שיטתית יותר מזו של אפלטון, והוא הפך אותה לתורה סדורה המאפשרת להבחין בין טיעונים מבוססים לטיעונים שאינם מבוססים על סמך זיהויה של הצורה הלוגית של הטיעונים. טיעון הוא תקף כאשר ההנחות מספיקות לשם תמיכה במסקנה, כך שלא ייתכן שההנחות אמיתיות אבל המסקנה שקרית. ההכרח הלוגי של הטיעונים התקפים נובע מכך שלטענות ישנו מבנה פנימי, למשל, שבכל טענה ישנו נושא ונשוא, ושכל טענה היא כללית או פרטנית, וישנו מספר מוגבל של צורות שבהן ניתן לקשר טענות זו לזו (למשל, טיעונים שבהם שתי ההנחות פרטניות, והמסקנה כללית, או כאלו שבהם אחת ההנחות כללית, השנייה פרטית, והמסקנה כללית, וכולי). מבין הצורות האפשריות של טיעונים בני שתי הנחות ומסקנה אחת, גילה אריסטו את הצורות של הטיעון התקף או המופתי, המוביל תמיד מהנחה אמיתית למסקנה אמיתית. אריסטו טען שבאמצעות צורות אלו משמשת הלוגיקה ככלי עבור המדע וכאמצעי להתקדמות הידע. קיים היום ויכוח האם, לפי אריסטו, הלוגיקה היא חלק ממשי מהפילוסופיה (כמו, למשל, האתיקה) או רק כלי עבודה (אורגנון) של הפילוסופים.
מושגי היסוד בלוגיקה האריסטוטלית הם: מונח, טענה, טיעון, נביעה או היסק, וכלל המרה. כמו כן ניתן להחיל בקלות על הלוגיקה האריסטוטלית את המונחים המודרניים של תקפות נאותות, וכלל היסק. תפקיד הלוגיקה הוא להבחין בטיעונים בעלי צורות תקפות, כלומר כאלו שבהם מהנחות אמיתיות נובעת מסקנה אמיתית. טיעונים שאינם עומדים בקריטריונים האלו, אינם טיעונים תקפים. ישנם כללי המרה המאפשרים להראות כי טענות שונות בצורתן הן למעשה שקולות זו לזו וכך להרחיב את מספר צורות הטיעון התקפות.
להלן נבחן תחילה את הרעיון שלטיעון יש צורה לוגית, לאחר מכן נדון בעקרונות היסוד של הלוגיקה אצל אריסטו, ולבסוף נדון במגבלותיה של הלוגיקה האריסטוטלית.
צורתו הלוגית של הטיעון
[עריכת קוד מקור | עריכה] ערך מורחב – סילוגיזם
ערך מורחב – סילוגיזם
טיעון הוא קבוצה של משפטים (או קבוצה של טענות) שחלקם הנחות ואחד מהם הוא המסקנה, והקבוצה נחשבת טיעון כאשר המעבר בין ההנחות למסקנה הוא תקף, כלומר כאשר המסקנה נובעת בהכרח מן ההנחות. מהי נביעה הכרחית? כאשר ניתן לומר שאין מצב עניינים שבו ההנחות אמיתיות אבל המסקנה שקרית, כלומר כאשר אין דוגמה נגדית. באמצעות הניתוח של מבנן הבסיסי של טענות, אריסטו זיהה כי לטיעונים בעלי שתי הנחות ומסקנה ישנו מספר סופי של צורות, וחלק מהן הן כאלו שמשמרות את האמת של ההנחות וכך מבססות את אמיתותה של המסקנה. לטיעונים כאלו קרא אריסטו סילוגיזם.
נוכל להבין את הרעיון של הצורה הלוגית של טיעון תקף אם נחשוב על ההבדל בין תקפות ואמיתות. לדוגמה: נתונות שתי הנחות:
- כל היוונים הם בני אדם.
- כל בני האדם הם בני תמותה.
מסקנה: כל היוונים הם בני תמותה.
התקפות של טיעון זה כמעט ברורה מאליה. ברור גם שאם שתי ההנחות אמיתיות, גם המסקנה, בהכרח, אמיתית. אין באפשרותנו להעלות על דעתנו מצב שבו ההנחות אמיתיות והמסקנה אינה אמיתית. אבל מה אם אחת ההנחות שקרית? או אז הטיעון עודנו תקף, אף שבמקרה כזה ייתכן שהמסקנה שקרית. אריסטו סבור כי הטיעון תקף בזכות צורתו, ללא קשר לשאלה האם חלק מהטענות שקריות מבחינת התוכן שלהן. ההבחנה בין טיעון תקף שבו ההנחות אמיתיות לטיעון תקף שבו ההנחות אינן אמיתיות היא ההבחנה בין נאותות (soundness) לאי-נאותות של הטיעון, אבל היא אינה משפיעה על תקפות הטיעון עצמה. צורתו הכללית של הטיעון הזה היא כזו:
- כל א הוא ב
- כל ב הוא ג
מסקנה: כל א הוא ג
יש לשים לב לכמה פרטים חשובים בנוגע לניתוח הצורני של מבנה הטיעון, על פי אריסטו. ראשית, ישנם בטיעון שלושה מונחים כוללים אשר כל טענה מקשרת בין שניים מהם. בטיעון תקף ישנו מונח מסוים (ב') אשר מופיע בהנחה הראשונה ומופיע שנית בהנחה השנייה, והוא המתווך בין שני המונחים (א' ו-ג'), אשר מופיעים כל אחד בהנחה אחת בלבד. במסקנה, המונח המתווך (ב') אינו מופיע כלל, ומה שהמסקנה מלמדת אותנו זה על הקשר שבין השניים האחרים (א' וג'). אריסטו הוא שהמציא את מתודת ההפשטה המאפשרת להציג מונחים באמצעות אותיות, וזהו צעד חשוב בדרך להמצאתו של המשתנה. כמו כן, יש לשים לב לכך שמלבד המונחים, המיוצגים באמצעות אותיות, מופיעים בגרסה הצורנית של הסילוגיזם קבועים לוגים, דהיינו מילים כגון "כל", "הוא" (האוגד), וכן מילים נוספות שעוד לא פגשנו בטיעון שלעיל, כגון "חלק מ" והשלילה באמצעות "אינו". כאשר אנו מצרינים את הטיעון אנו נפטרים אך ורק מן השמות של המונחים, ואילו הצורה הלוגית של הטיעון, המיוצגת באמצעות הקבועים הלוגיים, נשארת חשופה לעינינו.
מתפיסה זו של הצורה התקפה של הטיעון יוצא שאם בטיעון מסוים ההנחות אמיתיות והמסקנה שקרית אזי הטיעון אינו תקף. למשל בטיעון-לכאורה, שדומה לקודם:
- כל בני האדם הם בני תמותה.
- כל היוונים הם בני תמותה.
מסקנה-לכאורה: כל היוונים הם בני אדם.
נניח ששתי ההנחות אמיתיות. עדיין ייתכן שהמסקנה אינה נכונה, למשל אם אנו מוכנים להחשיב את סוסיהם של היוונים כיוונים. מכאן שבטיעון-לכאורה שבחנו ישנה בעיה - אין יחס של נביעה בין ההנחות והמסקנה. צורת הטיעון בה אנו מתבוננים איננה תקפה, וכל טיעון בעל אותה צורה יהיה טיעון בלתי תקף:
- כל א הוא ב.
- כל ג הוא ב.
מסקנה-לכאורה: כל ג הוא א.
כל טיעון בעל צורה כזו אינו תקף, והוא יכונה כשל לוגי.
עד עכשיו בחנו טיעונים שבהם כל הטענות הן טענות כלליות. אולם ישנם גם טיעונים תקפים המקשרים טענות פרטניות, כלומר כאלו שבחלק מהטענות המקושרות בהם הקבוע הלוגי אינו "כל" אלא "חלק מ". למשל:
- כל הפירות צומחים על עצים.
- חלק מהפירות הם הדרים.
מסקנה: חלק מהצומחים על העצים הם הדרים.
והנה צורת הטיעון:
- כל א הוא ב
- חלק מ-א הם ג
מסקנה: חלק מ-ב הם ג
ֿאריסטו הבחין גם בשלילה כאחד מן הקבועים הלוגים, וכך הבחין בין צורתן של טענות חיוביות ושל טענות שוללות. באמצעות כך הוא זיהה צורות נוספות של טיעונים תקפים, למשל:
- כל הנמרים הם יונקים.
- אף דג אינו יונק.
מסקנה: אף דג אינו נמר.
והנה צורת הטיעון:
- כל א הוא ב.
- אף ג אינו ב.
מסקנה: אף ג אינו א.
לאחר שבחן את מגוון הצירופים האפשריים של טענות (כלומר צירופים שבהם סדר המונחים זהה, או צירופים שבהם השילוב בין טענות כוללות ופרטניות, או בין טענות שוללות וחיוביות, דומה), הצליח אריסטו לצמצם את מספר הטיעונים התקפים היסודיים לארבעה, על ידי שימוש בשלושה כללי המרה שבאמצעותם ניתן להמיר טענות מסוג אחד בטענות מסוג אחר. אלו הם שלושת כללי ההמרה:
- מ"אין א שהוא ב" הסק: "אין ב שהוא א"
- מ"כל ב הוא א" הסק: "חלק מ-א הוא ב"
- מ"חלק מ-ב הוא א" הסק: "חלק מ-א הוא ב"
הערה נוספת: הניתוח של אריסטו מתייחס לטענות שבהן מקושרים שני מונחים כוללים, שמות של קבוצות. למעשה, הלוגיקה האריסטוטלית מועילה במיוחד לדון ביחסים בין מינים וסוגים (אריסטו החשיב את המחקר הטקסונומי בביולוגיה כצורה המופתית של המדע, ואת הסילוגיזם ככלי העבודה העיקרי של המדען). אולם הניתוח האריסטוטלי מאפשר להתייחס גם לשמות פרטיים כאילו היו מונחים כוללים, וכך להציג את הטיעון התקף הבא:
- כל בני האדם הם בני תמותה
- סוקרטס הוא אדם
מסקנה: סוקרטס הוא בן תמותה
עקרונות היסוד הלוגיים אצל אריסטו
[עריכת קוד מקור | עריכה]ניתן לזהות שני עקרונות לוגיים יסודיים המדריכים את אריסטו:
1) חוק אי-הסתירה - לחוק זה היבט אונטולוגי, היבט לוגי, והיבט פסיכולוגי. מן ההיבט האונטולוגי, דבר לא יכול, באותו זמן, מקום ונסיבות, לשאת תכונה מסוימת ולא לשאת את אותה תכונה בעת ובעונה אחת; מן ההיבט הלוגי או הסמנטי, טענה אינה יכולה להיות גם אמיתית וגם שקרית, ומן ההיבט הפסיכולוגי, לא ניתן לחשוב מחשבה ואת המחשבה המנוגדת לה בעת ובעונה אחת. העיקרון מופיע בספר המטפיזיקה של אריסטו כך (ע' בקר 1005b):
"לא אפשרי לאותה תכונה להשתייך ולא להשתייך לאותו דבר בו זמנית ובאותו יחס... אף אחד אינו יכול להניח כי אותו דבר הוא ואינו... ואם לא אפשרי לתכונות סותרות להשתייך בו זמנית לאותו עצם... ואם דעה הסותרת דעה אחרת מנוגדת לה, ברור כי אין זה אפשרי... להניח שדבר מסוים הוא ואינו בו זמנית וביחס לאותו עצם... ומכאן שכל אדם המדגים דבר כלשהו, מתייחס לעקרון זה כהנחה הראשונית, משום שזוהי מטבע הדברים נקודת המוצא לכל שאר האקסיומות"
2) חוק השלישי הנמנע - לפיו טענה יכולה להיות או אמיתית או שקרית, ואין שום אפשרות ביניים שלישית. מכאן, שהלוגיקה בוחנת טענות אך ורק אם יש להן אחת משני ערכי אמת: אמת ושקר. טענות שאינן כאלו אינן מעניינה של הלוגיקה; ובאשר לטענות שהלוגיקה כן עוסקת בהן, אין אופציה נוספת. לא תיתכן טענה שאינה אמת ואינה שקר, ולכן ביטוי כגון "או שדני אוהב ללכת לבית הספר או שדני לא אוהב ללכת לבית הספר" יחשב כנכון בהכרח, משום שאחד החלקים של המשפט חייב להתקיים.
חוק אי-הסתירה מאפשר להראות את שקריותה של טענה כאשר ניתן להסיק ממנה דבר והיפוכו; מכאן שבצירוף לחוק השלישי הנמנע, ניתן להראות את אמיתותה של טענה על ידי הוכחת שקריותה של שלילתה. הוכחה מסוג זה מכונה בלטינית רדוקציו אד אבסורדום (reductio ad absurdum) או הוכחה בדרך השלילה. מכיוון שבהוכחה כזו ההנחה (שלילתה של טענה מסוימת) מובילה לסתירה, ברור שההנחה אינה יכולה להיות אמיתית. ומכאן שהטענה המקורית (אותה שללנו כהנחה להוכחה על דרך השלילה) אמיתית.
כללים אלו ברורים מאליהם אך יש מקרים בהם הרלוונטיות שלהם אינה ברורה. לדוגמה, ישנם משפטים וטענות שאנו משתמשים בהם בחיי היומיום שאין להם בהכרח תשובה מוחלטת של "אמת" או "שקר". ניקח לדוגמה את השאלה מתי הופכת קבוצה של חפצים לערימה. למשל, כמה גרגרי חול דרושים על מנת להפוך לערימה? האם יש מספר מסוים של גרגרים שמעבר לו מדובר בערימה? או ששאלה זו אינה ניתנת למענה חד משמעי, והטענה כי קבוצה של גרגרי חול היא ערימה אינה כפופה לחוק השלישי הנמנע? הלוגיקה הקלאסית נמנעת מלעסוק בטענות מסוג זה, שכן היא מקבלת את החוקים הללו כהנחות יסוד. במאה העשרים התפתח ענף בלוגיקה המכונה אינטואיציוניזם, ובו דוחים את עקרון השלישי הנמנע. בענף אחר וחדש יחסית של הלוגיקה, לוגיקה עמומה (Fuzzy logic), עוסקים בטענות שאינן אמיתיות או שקריות באופן חד-משמעי.
מגבלות הלוגיקה האריסטוטלית
[עריכת קוד מקור | עריכה]מנקודת המבט של הלוגיקה המודרנית, ללוגיקה של אריסטו מגבלות רבות, והיא אינה מצליחה להביע את שלל היחסים הלוגיים המופיעים בטענות המשמשים אותנו לשם הסקת מסקנות.
בין השאר, אריסטו הכיר אך ורק במבנה של טענות שיש בהן נושא ונשוא (א הוא ב), ולא הכיר בטענות שצורתן צורת התנאי (אם א אז ב). הוא אף סבר שבטיעון תקף חייבת להיות יותר מהנחה אחת, ושהמסקנה חייבת להיות שונה מההנחות. ואולם הגדרתו לטיעון תקף אינה נותנת לנו סיבה לפסול את תקפותו של הטיעון הבא:
הנחה: המלך הוא עירום. מסקנה: המלך הוא עירום.
אין מצב שבו ההנחה אמיתית ואילו המסקנה שקרית, ועל כן הטיעון תקף (אם כי הוא טיעון שאין בו כל עניין).
אחד ההבדלים הברורים בין הלוגיקה האריסטוטלית לבין הלוגיקה החדשה נוגע להנחת הקיום, אשר מתפקדת אצל אריסטו כך שכל מונח, אשר יכול להופיע בטענה, נחשב כאילו אינו ריק, כלומר כאילו קיימים ישים מסוימים השייכים לו. למשל, כאשר הטענה היא "כל בני האדם הם בני תמותה", ניתן על פי הלוגיקה האריסטוטלית להסיק "ישנו בן אדם". בחוק ההמרה השני של אריסטו ישנה הרשאה מפורשת למעבר מן הטענה "כל ב הם א" לטענה "יש א שהוא ב". לעומת זאת, בלוגיקה החדשה, השימוש בכמת האוניברסלי אינו מבטיח שהפרדיקט אשר מצוי בטווח שלו אינו מציין קבוצה ריקה.
אריסטו גם אינו מכיר באופיים הייחודי של יחסים, דהיינו של פרדיקטים המקשרים שני אובייקטים. לפיכך, לא ניתן להביע באמצעות הלוגיקה האריסטוטלית את הקשרים הלוגיים שבין הטענות הבאות:
- יוני הוא אביו של רוני
- רוני הוא אביו של בוני
- יוני הוא אביו של אביו של בוני
לו היינו מנסים להביע את הטענות הללו באמצעים אריסטוטליים, היינו מקבלים את הצורה הלא-תקפה הבאה:
- א הוא ב
- ב הוא ג
- א הוא ד
בעוד שאופן הניתוח של המבנה היסודי של הטענה אצל אריסטו אינה נדחית לגמרי בצורתו הפשוטה של תחשיב הפסוקים המודרני, הרי שהלוגיקה המודרנית, מאז פרגה, מציעה ניתוחים מתוחכמים בהרבה של המבנה הפנימי של הטענה באמצעות תחשיב הפרדיקטים. בעוד שאריסטו סבר כי לטענות יש שלושה חלקים: שני מונחים והאוגד המחבר ביניהם, בתחשיב הפרדיקטים של הלוגיקה החדשה הטענה האטומית היא בעלת שני חלקים בלבד: האובייקט והפרדיקט המושת עליו. בנוסף, הלוגיקה החדשה אינה תופסת את הכמת הלוגי כמאפיין את הטענה כולה או את האוגד, אלא כחל על משתנה מסוים מתוך הטענה. באמצעות כך שהכמתים יכולים כעת להופיע כחלק מן המבנה הפנימי של הטענה, ובאמצעות כך שניתן כעת לנסח טענות שיש בהם כימות מרובה של מספר משתנים בעת ובעונה אחת, מאפשרת הלוגיקה החדשה להביע עובדות וקשרים שאינם ניתנים להבעה באמצעות הניתוח האריסטוטלי. כך למשל הצליחה הלוגיקה המודרנית לתת לראשונה תיאור מדויק של מושג הגבול באנליזה המתמטית של פונקציות, שכן לשם הבעת מושג זה יש צורך בטענה מרובת כמתים מן הצורה "לכל ε קיים δ כך ש...".
הלוגיקה לאחר אריסטו ועד המאה התשע עשרה
[עריכת קוד מקור | עריכה]במשך כאלפיים שנה נחשבה הלוגיקה האריסטוטלית כמשהו שאין כל צורך לפתחו או לשנותו, אף שנעשו מעט תוספות מינוריות למטרות דידקטיות. ואולם, כבר בסוף המאה השמונה עשרה, אצל קאנט, ניכרת חוסר נוחות הולכת וגוברת באשר ליכולתה של הלוגיקה האריסטוטלית לתאר את כל אופני המחשבה התקפים. קאנט ביקר את הלוגיקאים הסכולסטים על כך שצורת הטענה היחידה בה הם מטפלים היא טענה של נושא-נשוא (א הוא ב). קאנט הציע להחשיב גם את הצורות של משפט התנאי (אם א אז ב) ושל המשפט הדיסיונקטיבי (א או ב) כצורות יסודיות של טענות.
החל במאה התשע-עשרה, התפתחות הלוגיקה הייתה תלויה במידה רבה בעניין שגילו בה מתמטיקאים, אשר ביקשו להבין את אופיין של טענות מתמטיות (למשל משוואות, שצורתן אינה כזו של נושא-נשוא) ואת אופיו של הטיעון המתמטי, דהיינו ההוכחה. במקביל לחקירת המאפיינים הלוגיים של המתמטיקה, החל שימוש במתודות מתמטיות בלוגיקה, וההפריה ההדדית בין שני המדעים גברה. מתמטיקאים ופילוסופים כמו ג'ורג' בול, אוגוסטוס דה מורגן, ויליאם סטנלי ג'בונס, צ'ארלס פירס, וארנסט שרדר, הניחו במחקריהם את היסודות ללוגיקה המודרנית. עבודתם של בול וממשיכיו עומדת ביסוד תחשיב הפסוקים המודרני, וגישתם האלגברית ללוגיקה עומדת ביסוד מדעי המחשב. בול וממשיכיו הציגו לראשונה מונחי יסוד של תורת הקבוצות במסגרת הדיון בלוגיקה, ובאמצעותם ייצגו הסקים אריסטוטליים כמשוואות שהמסקנה היא פתרונן. במקביל, מתמטיקאים ופילוסופים כמו ברנרד בולצאנו ואלקסיוס מיינונג חקרו את מושג הטענה ואת האופן בו תפיסותינו את האובייקטיביות של הלוגיקה והמתמטיקה מחייבות אותנו לקבל את קיומן האידיאלי של טענות. התפתחויות אלו עומדות בבסיס עבודתו של גוטלוב פרגה, שאף שעיקר הישגיו בלוגיקה הושגו במאה התשע-עשרה, הם כמעט לא נודעו עד תחילת המאה העשרים.
הלוגיקה של פרגה
[עריכת קוד מקור | עריכה]גוטלוב פרגה נחשב הדמות הבולטת ביותר בלוגיקה מאז ימי אריסטו. אף על פי שעבודתו לא הוכרה כמעט בימי חייו, רעיונותיו קיבלו תהודה בעיקר דרך מי שהושפע ממחקרו וכתביו בעיקרם ג'וזפה פאנו, ברטראנד ראסל ולודוויג ויטגנשטיין.
חידושיו של פרגה
[עריכת קוד מקור | עריכה]"כתב מושגים", ספרו הראשון והמהפכני של פרגה מ-1879, סימן את תחילתה של תקופה חדשה בהיסטוריה של הלוגיקה. בספר זה הציע פרגה לראשונה אקסיומטיזציה של תחשיב הפסוקים ושל תחשיב הפרדיקטים, המנתח את מבנה הטענה כבעלת שני חלקים בלבד. בעוד שאריסטו סבר כי לטענות יש שלושה חלקים: שני מונחים והאוגד המחבר ביניהם ("א' הוא ב'", או "כל א' הוא ב'"), בתחשיב הפרדיקטים של הלוגיקה החדשה הטענה האטומית היא בעלת שני חלקים בלבד, פרדיקט ואובייקט, החוברים זה לזה כפי שפונקציה חלה על משתנים.
שיטת התיווי הלוגי של פרגה לא התקבלה, גם כאשר רעיונותיו נתקבלו במסורת. למשל, את המשפט "דני הוא חכם", ניתן להצרין[1] בעקבות פרגה בתור , כאשר F מציין את הפרדיקט חכם, ו-a מציין את שמו של האובייקט, דני.
שיטתו של פרגה מאפשרת גם להביע יחסים בין שני אובייקטים או יותר באמצעות פרדיקטים דו מקומיים – פרדיקטים שמקבלים שני אובייקטים. למשל, כדי לומר שדני (a) הוא חבר של רני (b), תוך ציון יחס החברות באמצעות האות R, כותבים: .
פרגה תרם תרומה הכרחית למתמטיקה וללוגיקה באמצעות המצאת תורת הכימות (קוונטיפיקציה). הלוגיקה החדשה אינה תופסת את הכמת הלוגי כאפיון של הטענה כולה או של האוגד שלה, אלא כפונקציה מסדר גבוה יותר החלה על הפרדיקט ועל המשתנה שלו. למשל, את צורתה של הטענה "כל דבר הוא חכם" ניתן להביע לפי פרגה בתור:
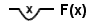
(בשיטה המודרנית מסמנים זאת: ), והטענה "יש דבר אחד לפחות שהוא חכם" תובע בצורה

(בשיטה המודרנית מסמנים: , או באופן שקול: ).
באמצעות התחביר החדש של תחשיב הפרדיקטים, הכולל כימות, יכולים הכמתים להופיע כחלק מן המבנה הפנימי של הטענה, ובאמצעות כך ניתן כעת לנסח טענות שיש בהם כימות מרובה של מספר משתנים בעת ובעונה אחת. טכניקות אלו מעניקות ללוגיקה החדשה כוח להביע עובדות וקשרים שאינם ניתנים להבעה באמצעים האריסטוטלים. למשל, הלוגיקה המודרנית הצליחה לתת לראשונה תיאור פורמלי של מושג האינסוף – מושג שהוביל לפרדוקסים מאז ימי האסכולה האלאטית – ושל מושג הגבול באנליזה המתמטית של פונקציות, שכן לשם הבעת מושגים אלו יש צורך בטענה מרובת כמתים מן הצורה "לכל ε קיים δ כך ש...". לשם המחשה, אם נשתמש שוב בסימן היחס בין חברים כפרדיקט דו-מקומי, R, אז ניתן להצרין את הטענה "לכל אחד יש חבר" בתור:
הפילוסופיה של הלוגיקה של פרגה
[עריכת קוד מקור | עריכה]בפילוסופיה של הלוגיקה, פרגה מציג את שלושת העקרונות היסודיים שלו בהקדמה לספרו השני, "יסודות האריתמטיקה". העיקרון הראשון מציג את התנגדותו של פרגה לפסיכולוגיזם, דהיינו לעירוב של שיקולים פסיכולוגיים בניתוח הרעיונות הלוגיים היסודיים. הוא סבר כי חוקי הלוגיקה אינם רק חוקי המחשבה, אלא חוקי האמת, ושיש לתכנים לוגיים קיום אובייקטיבי, ולא סובייקטיבי ותלוי במבנה האמפירי של המוח האנושי. מבחינה זו, פרגה היה ריאליסט בנוגע לישויות אידיאליות, כולל הישויות המתמטיות הבסיסיות ביותר - המספרים. העיקרון השני מציג את עקרון הקונטקסט (הרלוונטי גם בפילוסופיה של הלשון) - לפיו מילה מקבלת את משמעותה רק בקונטקסט של השיפוט שהיא משמשת כחלק ממנו. העיקרון השלישי מציג את ההבחנה בין מושג לבין מושא. על פי פרגה, מושגים הם פונקציות, המקבלות את משמעותן רק כאשר ניתן להן אובייקט כערך שלהן. כשלעצמו, המושג הוא בלתי רווי (unsaturated), ורק כשהוא מתחבר לשם או לשם של משתנה, הוא מקבל משמעות. כך פותר פרגה את בעיית אחדות הטענה שהטרידה אחר כך את ראסל, ומציע, באופן מובלע, תורת טיפוסים פרימיטיבית: מושגים (מסדר ראשון) חלים על אובייקטים בלבד, משום שרק באמצעותם הם נהיים רוויים במשמעות. אולם מכאן עולות גם כמה מסקנות פרדוקסליות. מכיוון שרק בצירוף לשם או למשתנה יש למושג משמעות, המושג אינו יכול להופיע כנושא במשפט. מכאן יוצא, כי אין אפשרות לומר "המושג סוס הוא מושג", משום שכאן המושג סוס מופיע כאובייקט, ולא כמושג. פרגה נאלץ לפיכך לטעון: "המושג סוס אינו מושג", ומכאן נובע (אם כי פרגה אינו אומר זאת מפורשות): "המושג מושג אינו מושג". הטענה הפרדוקסלית חושפת כיצד שלושת העקרונות של פרגה קשורים זה לזה. לאור עקרון הקונטקסט, פרגה אינו מוכן לקבל שלפרדיקט יש משמעות במנותק מן המסגרת הטענתית בה הוא מופיע, ובה הוא רווי בזכות קישורו לאובייקט. לאור התנגדותו לפסיכולוגיזם, פרגה שולל את ההתייחסות אל המושג כאובייקט וסבור שהתייחסות כזו נובעת מתפיסת המושג כתוכן מנטלי אינרטי, ולא כפונקציה. עם זאת יש לפרגה דרכים לטפל במושגים במסגרת לוגיקה מסדר שני. דרך אחת היא על ידי ציון האקסטנציה של המושגים (ranges of values או Wertverläufe), דהיינו הקבוצה של האובייקטים שעבורם המושג מעניק ערך אמיתי. קבוצה זו נתפשת כמושא, והיא יכולה להופיע, למשל, בטענות שוויון מספרי. טענות כגון אלו, המכריזות על שוויון מספרי בין האקסטנציות של מושגים שונים הן מהותיות עבור ההגדרה הלוגית של מושג המספר – הגדרה שמקורה אצל פרגה.
פרגה היה התומך המשמעותי הראשון של לוגיציזם – העמדה לפיה ניתן לצמצם את המתמטיקה כולה ללוגיקה. פרגה אף ניסה להוכיח כי חוקי האריתמטיקה, ומושג המספר עצמו, ניתנים לפיתוח מתוך אקסיומות שאותן תפס פרגה כלוגיות במובהק. לאחר שפורסם הכרך הראשון של ספרו השלישי, "חוקי היסוד של האריתמטיקה", ברטראנד ראסל גילה את הפרדוקס של ראסל, והצליח להראות שהאקסיומות של פרגה, ובמיוחד אקסיומה מספר חמש, מובילות אליו (מן האקסיומה החמישית נובע כי עבור כל מושג, יש אובייקט המהווה את האקסטנציה של מושג). הוא כתב על כך לפרגה, שהוסיף נספח לכרך השני של הספר בו הוא מודה כי אין לו פתרון מספק לבעיה, והוא לא הצליח לתקן את עבודתו על מנת למנוע את הפרדוקס. בפרסומים מאוחרים יותר של ראסל ושל ג'ון פון נוימן מוצע פתרון לבעיה באמצעות תורת הטיפוסים (theory of types).
לוגיקה בת ימינו
[עריכת קוד מקור | עריכה]באמצעות פיתוחם של אמצעים סימבולים חדשים להבעת היחסים הלוגיים בין חלקי הטענה, ובאמצעות גילוין של דרכים חדשות להבין את מבנה העומק של הטענות, הפכה הלוגיקה המודרנית לכלי רב עוצמה באמצעותו ניתן לבחון טיעונים מורכבים יותר מאלו שהלוגיקה האריסטוטלית עסקה בהם; לתת ניתוחים יסודיים של טענות מתמטיות מורכבות; ולזהות תכונות צורניות לא רק של הטענה ושל הטיעון, אלא גם של מערכות לוגיות שלמות, תכונות כגון שלמות, נאותות, כריעות וקומפקטיות, שהן תכונות הנוגעות לאפשרויות ההבעה הגלומות בשפה מסוימת או במערכת אקסיומטית מסוימת, ולא תכונות של טענה או של קבוצה מסוימת של טענות. הלוגיקה המודרנית סיפקה, באמצעים אלו, את היסודות למדעי המחשב ואפשרה את פיתוחם של המחשבים המודרניים.
בעקבות פרגה, פרח המחקר הלוגי במאה העשרים בעבודתם של ברטראנד ראסל, לודוויג ויטגנשטיין, אלפרד טרסקי, קורט גדל, אלן טיורינג, ואחרים. במרבית המקרים הייתה עבודתם רלוונטית הן לפילוסופים והן למתמטיקאים, שכן היא עסקה ביסודות המשותפים לכל שפה ולכל מערכת לוגית באשר היא. למעשה, התנועה המובילה בלוגיקה בתחילת המאה העשרים, הלוגיציזם, ביקשה להראות כי המתמטיקה מבוססת על הלוגיקה. ראסל, למשל, סבר כי בעיות היסוד של המתמטיקה אינן מעניינו של המתמטיקאי, אלא של הפילוסוף והלוגיקאי.
הלוגיקה המודרנית היא לוגיקה סימבולית, דהיינו היא בוחנת צורות מופשטות המיוצגות באמצעות סמלים, שניתן להבין אותן כמייצגות את הצורות של הטענות וההיסקים שאנו מכירים מן השימוש הטבעי בשפה. בלוגיקה מנסחים ובוחנים מערכות לוגיות בשפה הסימבולית. מערכת לוגית היא תחשיב (calculus) בו ניתן לבצע הוכחות. שני התחשיבים הלוגיים הבסיסיים הם תחשיב הפסוקים (propositional calculus או sentential calculus) ותחשיב הפרדיקטים (predicate calculus). תחשיב הפסוקים הוא הרחבה פשוטה למדי של הלוגיקה הקלאסית, ואילו תחשיב הפרדיקטים בוחן את המבנה הפנימי של הטענות ומאפשר שימוש בכמתים, ובכך מעניק ללוגיקה כוח ביטוי שאינו בר השוואה לזה של הלוגיקה האריסטוטלית. התחשיב הוא מערכת פורמלית שיש בה נוסחאות בנויות כהלכה (נב"כ) מבחינה תחבירית, שחלקן מקבלות מעמד מיוחד של אקסיומות, וכן מערך של כללי היסק הקובעים אילו נוסחאות ניתן לגזור מאילו, ובכך להוכיח אותן. התחביר של התחשיב מגדיר באופן רקורסיבי את כל הנב"כים של התחשיב.
בלוגיקה המודרנית, נהוג להבחין בין התחביר (syntax) של המערכת, הקובע מהו משפט תקני ומהם הכללים לגזירה של משפט אחד ממשנהו, ובין הסמנטיקה (semantics) שלה, הקובעת את ערכי האמת של המשפטים שניתן ליצור באמצעות השפה של המערכת. אם מדובר בשפה כמו תחשיב הפסוקים, הסמנטיקה מספקת ערך אמת לכל אחד מן הפסוקים היסודיים, והיא מספקת פירוש סמנטי לפעולתם של כל אחד מן הקשרים הלוגיים, למשל באמצעות טבלת אמת המציגה כיצד משפט מורכב מקבל את ערך האמת שלו על בסיס ערכי האמת של המשפטים שהוא מחבר זה לזה. בשפות לוגיות מורכבות יותר, דוגמת תחשיב הפרדיקטים, הסמנטיקה קובעת מהי קבוצת האיברים של תחום הדיון, מהן הקבוצות של האובייקטים המשויכים לכל פרדיקט (דהיינו, לאילו אובייקטים יש את התכונה שהפרדיקט מייצג), וכן את הפירוש של הקשרים הלוגיים. כל פירוש סמנטי של מערכת כזו הוא מודל, אולם התכונות הלוגיות של המערכת עצמה צריכות להיות תקפות עבור כל מודל אפשרי. לדוגמה, תקפות לוגית של טיעון חייבת להיות תלויה בצורה הלוגית של הטענות המקושרות בו, ללא קשר לפירוש שאנו נותנים למונחים הלא-לוגיים המופיעים בהן.
מכאן שהלוגיקה המודרנית עוסקת בבחינת תכונותיהן הצורניות של מערכות לוגיות, הן מבחינת התחביר שלהן והן מבחינת הסמנטיקה שלהן. למחקר כזה קוראים מטא-לוגיקה. מבין התכונות הצורניות החשובות ביותר של מערכות לוגיות, ניתן להזכיר את התכונות הבאות, אשר את קיומן עבור מערכות מסוימות ניתן להוכיח או לשלול:
- עקביות (consistency) - זוהי תכונתן של מערכות לוגיות שאין סתירה בין אי אלו מן הטענות השייכות להן.
- שלמות (completeness) - זוהי תכונתן של מערכות לוגיות שבהן לגבי כל נוסחה אמיתית, ניתן לספק לה הוכחה מן האקסיומות.
- נאותות (soundness) - בניגוד לנאותות של טיעון, שהיא התכונה של טיעון תקף שבו כל ההנחות אמיתיות, נאותות של מערכת לוגית היא התכונה לפיה אם נוסחה מסוימת ניתנת להוכחה מן האקסיומות על פי חוקי התחשיב, אזי נוסחה זו אמיתית.
הוכחות לשלמות ולנאותות מעידות על הזיקה שבין התחביר והסמנטיקה של המערכת. התחביר קובע איזו נוסחה היא תיאורמה (או משפט), דהיינו איזו נוסחה ניתנת לגזירה מן האקסיומות, באמצעות כללי ההיסק. הסמנטיקה קובעת איזו נוסחה היא טאוטולוגיה, דהיינו איזו נוסחה היא אמיתית בהכרח מכוח משמעותם של המונחים המקושרים בה והאופן בו הם מקושרים. לפי הגדרות אלו, למערכת יש שלמות, כאשר כל טאוטולוגיה היא גם תאורמה. למערכת יש נאותות, כאשר כל תיאורמה היא טאוטולוגיה.
ניתן לראות כי התכונות נאותות ושלמות קשורות זו לזו, אף שלא כל מערכת נאותה היא גם שלמה. קורט גדל הוכיח ב-1931 שבמערכות לוגיות שהן חזקות מספיק (כאלו שכוללות את האריתמטיקה בתוכן, כמו המערכת שהציע ברטראנד ראסל בפרינקיפיה מתמטיקה), יש נוסחאות אמיתיות שלא ניתן להוכיח אותן או להפריך אותן. משפט מתמטי זה נקרא משפט האי-שלמות של גדל.
תחשיב הפסוקים
[עריכת קוד מקור | עריכה] ערך מורחב – תחשיב הפסוקים
ערך מורחב – תחשיב הפסוקים
תחשיב הפסוקים מאפשר לייצג את הקשרים בין ערכי האמת של טענות (פסוקים) שונות. תחשיב הפסוקים אינו מתחשב בטענות אלא שאם יש להן ערכי אמת, דהיינו הוא אינו בוחן את הצורה הפנימית של הטענות, ואת הקשרים שהן מציגות, למשל, בין אובייקטים (בתחשיב הפרדיקטים, הנידון להלן, יש ניתוח של מבנה עומק זה). הסמנטיקה של תחשיב הפסוקים מורה לנו כיצד עלינו להבין את היחס בין הסמלים המייצגים פסוקים שונים, ובין טענות מן השפה הטבעית. כאשר אנו מעוניינים לנתח טיעון בשפה הטבעית באמצעות תחשיב הפסוקים, הצעד הראשון שעלינו לעשות מכונה הצרנה'. בתהליך זה מסמנים כל משפט חיווי בסיסי (למשל 'השמש תזרח מחר' או 'יוסי גר בלונדון') בסימן קבוע (בדרך כלל אות אנגלית גדולה כמו P או Q, או הסימן Pi עם האינדקס i, המייצג מספר מסוים). סימן זה משמש לייצג את הטענה בכל מקום שתופיע בטיעון, והוא מכונה "פסוק יסודי", או "פסוק אטומי". תחשיב הפסוקים אינו עוסק בשאלה כיצד נקבע ערך האמת של פסוקים אטומיים, אלא בשאלה כיצד נקבע ערך האמת של פסוקים מורכבים יותר, המורכבים ממספר פסוקים אטומיים באמצעות קַשַּרים לוגיים. ערך האמת של הפסוקים האטומיים יכול להיקבע על ידי הפירוש הסמנטי שאנו נותנים לאותיות הפסוקיות; אולם ניתן גם להשאיר אותו כמשתנה, ולבחון כך את כלל היחסים האפשריים בין הטענות המורכבות, עבור כל הצבה של ערכי אמת לאותיות הפסוקיות. באמצעות הכללה כזו ניתן לקבוע כי טיעונים הם תקפים, כאשר עבור כל הצבה של ערכי אמת לפסוקים האטומיים המרכיבים את ההנחות, כאשר הצבה כזו עושה את ההנחות של הטיעון לאמיתיות, היא גם עושה את המסקנה לאמיתית.
תחביר לתחשיב הפסוקים
[עריכת קוד מקור | עריכה]תחשיב פסוקים מסוים כולל קבוצה של "פסוקים יסודיים" או "פסוקים אטומיים", ומספר קָשַרים לוגיים סטנדרטיים. לדוגמה, נגדיר ש P מייצג את הטענה "הגביע הוא שלנו", ו-Q מייצג את הטענה "אנחנו במפה"'. או אז ניתן להדגים את התחביר של חמשת הקשרים הלוגיים כך:
- שלילה: - זהו קשר אונרי, דהיינו הוא מקושר לאות פסוקית אחת בלבד. לדוגמה, מייצג את "הגביע הוא לא שלנו".
- קוניונקציה ("וגם"): או & - קשר בינארי, מקשר בין שני פסוקים. לדוגמה, הפסוק המורכב מייצג את הטענה "הגביע הוא שלנו ואנחנו במפה".
- דיסיונקציה ("או"): - קשר בינארי, מקשר בין שני פסוקים. לדוגמה, הפסוק המורכב מייצג את הטענה "הגביע הוא שלנו או אנחנו במפה".
- תנאי ("אם-אז"): - קשר בינארי, מקשר בין שני פסוקים. לדוגמה, הפסוק המורכב מייצג את הטענה "אם הגביע הוא שלנו אז אנחנו במפה".
- תנאי כפול ("אם-ורק-אם"): - קשר בינארי, מקשר בין שני פסוקים. לדוגמה, הפסוק המורכב מייצג את הטענה "הגביע הוא שלנו אם ורק אם אנחנו במפה".
הסמנטיקה של הקשרים הקלסיים מאפשרת להביע חלק מן הקשרים במונחים של הקשרים האחרים, וכך לבנות גרסאות שונות של תחשיבי פסוקים, שצורתם שונה אך זהים מבחינת כוח הביטוי שלהם, באמצעות בחירה שונה של הקשרים המשתתפים. לדוגמה, אפשר להביע את קשר התנאי ("אם A אז B") באמצעות דיסיונקציה ושלילה ("B או לא-A"). כללי דה-מורגן מאפשרים להביע דיסיונקציה במונחים של קוניונקציה ושלילה, וקוניונקציה במונחים של דיסיונקציה ושלילה. וכו'. תחשיב פסוקים שלם (או קבוצה שלמה של קשרים) הוא קבוצת קשרים שאפשר להציג באמצעותה כפסוק כל פעולה בוליאנית או כל טבלת אמת. ניתן להגדיר שני קשרים לא קלאסיים, שכל אחד מהם מאפשר בעצמו תחשיב פסוקים שלם. קשרים אלו הם הקשרים קו-שפר ("לא-וגם", NAND) ו"לא-או" (NOR). למשל, באמצעות התנאי והשלילה, נביע את הקשרים האחרים כך:
- מוגדר כ-
- מוגדר כ-
- מוגדר כ-
סמנטיקה לתחשיב הפסוקים
[עריכת קוד מקור | עריכה] ערך מורחב – טבלת אמת
ערך מורחב – טבלת אמת
במסגרת הסמנטיקה של תחשיב הפסוקים, כל פסוק יסודי יכול לקבל אחד משני ערכי אמת: "אמת" או "שקר", ובלבד שהוא מקבל את אותו ערך בכל הופעה שלו באותו טיעון. כל קשר לוגי מובן כפונקציית-אמת, דהיינו עבור כל צירוף של ערכי אמת, מחזיר הקשר ערך אמת אחד ויחיד. לדוגמה, השלילה מחזירה פסוק שקרי עבור כל פסוק אמיתי אליו היא מקושרת, ומחזירה פסוק אמיתי עבור כל פסוק שקרי. נוח לייצג פונקציות אמת באמצעות טבלת אמת, בהן T ו-F מייצגים את הערכים אמת ושקר, בהתאמה (באלגברה בוליאנית יוחלפו אלו בערכים 1 ו-0 בהתאמה). בטורים הימניים של הטבלה אנו ממצים את כלל הצירופים האפשריים של ערכי האמת הניתנים לפסוקים היסודיים, ובטורים השמאליים אנו מציגים את ערך האמת המתקבל עבור הפסוק המורכב:
טבלת האמת של שלילה
|
טבלת האמת של התנאי
|
טבלת האמת של הקוניונקציה
|
טבלת האמת של הדיסיונקציה
|
טבלת האמת של התנאי הכפול
|
כל שיוך של ערכי אמת לפסוקים יסודיים נקרא פירוש ("אינטרפרטציה") או הצבה. בטבלאות האמת, כל שורה היא פירוש. פסוק מורכב המקבל את הערך "אמת" בכל פירוש של הפסוקים היסודיים (כלומר כזה שבטבלת האמת שלו הוא מקבל T בכל השורות, נקרא טאוטולוגיה. משמעות הדבר היא שפסוק זה הוא אמיתי בזכות הקשרים הלוגיים שבין רכיביו, ללא תלות באמיתותם של הפסוקים האטומיים עצמם. פסוק המקבל את הערך "שקר" בכל פירוש נקרא סתירה. פסוק הוא קונטינגנטי אם ורק אם אינו סתירה ואינו טאוטולוגיה. קבוצה של פסוקים נקראת עקבית (קונסיסטנטית) אם קיים פירוש עבורו כל הפסוקים בקבוצה מקבלות ערך "אמת".
טבלאות אמת הן כלי נוח לשם בדיקת תקפותם של טיעונים (היסקים) בתחשיב הפסוקים. הטכניקה של טבלאות אמת מאפשרת לבטא את ערכי האמת של כל פסוק מורכב במונחי ערכי האמת של הפסוקים המרכיבים אותו, וכאשר הטבלה גמורה, ניתן לבדוק האם ישנם מצבים בהם ההנחות של הטיעון אמיתיות אבל המסקנה שקרית. אם יש שורה כזו בטבלה, הרי שהטיעון אינו תקף, שהרי זו דוגמה נגדית. אולם אם אין שורה כזו, הראנו שהטיעון תקף.
מערכות הוכחה לתחשיב הפסוקים
[עריכת קוד מקור | עריכה]ניתן לבנות לתחשיב הפסוקים מערכות הוכחה, שבהן ניתן להוכיח מקבוצת טענות נתונה טענות נוספות שנובעות ממנה. מערכות היסק אלה בנויות מכללים סינטקטיים (תחביריים) טכניים בלבד. המערכת הפשוטה ביותר מכונה מערכת הדדוקציה הטבעית, המכילה עשרה כללי היסק. עבור כל אחד מחמשת הקשרים היא מכילה כלל הכנסה (Introduction) וכלל הוצאה (Elimination). מערכת זו היא נאותה (כלומר, כל נוסחה שניתנת להוכחה, היא אמיתית) ושלמה (כלומר, כל נוסחה אמיתית גם ניתנת להוכחה מקבוצה זו במערכת).
תחשיב הפרדיקטים
[עריכת קוד מקור | עריכה] ערך מורחב – תחשיב הפרדיקטים
ערך מורחב – תחשיב הפרדיקטים
תחשיב פרדיקטים מסדר ראשון הוא מערכת אקסיומטית המאפשרת לטפל בפסוקים שהמבנה הבסיסי שלהן כולל נשואים (פרדיקטים) החלים על אובייקטים, או על משתנים שערכיהם הם אובייקטים. הפרדיקטים עצמם הם פונקציות המחזירות ערך אמת (אמיתי או שקרי) עבור אובייקטים מסוימים או עבור משתנים מסוימים. בתחשיב פרדיקטים מסדר גבוה יותר, פרדיקטים יכולים לחול על פרדיקטים אחרים וכמתים יכולים לחול על פרדיקטים. במתמטיקה תחשיב הפרדיקטים מופיע כשפה מסדר ראשון או כשפה מסדר שני.
תחביר של תחשיב הפרדיקטים
[עריכת קוד מקור | עריכה]גם בתחשיב הפרדיקטים נעשה שימוש בכל הקשרים הלוגיים הסטנדרטיים המוכרים מתחשיב הפסוקים (או בחלק מהם, ובלבד שתיווצר קבוצה שלמה של קשרים באמצעותה ניתן להביע כל פעולה בוליאנית): . בנוסף מופיעים בתחשיב שני כמתים, הוא הכמת הישי, המביע שפרדיקט מסוים מחזיר אמת עבור אובייקט אחד לפחות מתוך התחום. הוא הכמת הכולי או האוניברסלי, המציין כי עבור כל אובייקט בתחום, פרדיקט מסוים מחזיר ערך אמת.
הסמלים של תחשיב הפרדיקטים מציינים משתנים (מצוינים באותיות x,y,z עם או בלי אינדקס ממוספר), קבועים (שמות, המצוינים באותיות a,b,c וכו') ופרדיקטים (מצוינים באותיות גדולות Px, Rxy, וכו'), וכן קבועים לוגים (הקשרים והכמתים) וסימני פיסוק (סוגריים). לעיתים כוללים את יחס הזהות בסימני התחשיב וכך נעשה להלן.
את הנוסחאות הבנויות היטב של התחשיב ניתן להגדיר באינדוקציה ע"פ חמשת הכללים התחביריים (סינטקטיים) הבאים:
- אם P הוא פרדיקט המקבל n ארגומנטים, (P(t1,...,tn היא נוסחה בנויה היטב
- אם t1 ו-t2 הם שמות או משתנים, אז t1 = t2 היא נוסחה בנויה היטב
- אם φ נוסחה בנויה היטב, אזי φ היא נוסחה בנויה היטב
- אם φ ו-ψ נוסחאות בנויות היטב, אז לכל קשר כך ש , הרי ש (ψφ) היא נוסחה בנויה היטב (דהיינו עבור כל שני פסוקים אטומים, הצבתו של אחד מן הקשרים הבינריים ביניהם יוצרת נוסחה בנויה היטב).
- אם φ היא נוסחה ו-x הוא משתנה, φ ו- φ הם נוסחאות בנויות היטב
תפקידם של הסוגריים למנוע דו-משמעות בקריאה של המשפטים. עם זאת מקובל להשמיט את הסוגריים החיצוניים ביותר. כאשר בנוסחה כל המשתנים הם קשורים, דהיינו כאשר כל משתנה מצוי בטווח של כמת מתאים, הנוסחה נחשבת כפסוק (או טענה). או אז ניתן ליחס לה ערך אמת, בתלות בפירוש שהסמנטיקה נותנת לפרדיקטים ולתחום האובייקטים.
בתחשיב הפרדיקטים הפסוק היסודי (או הפסוק האטומי) הוא בעל שני חלקים בלבד, פרדיקט ואובייקט, החוברים זה לזה כפי שפונקציה חלה על משתנים. דוגמאות לפסוקים כאלו ניתנות לעיל, בסעיף הלוגיקה של פרגה. כוחו של תחשיב הפרדיקטים ניכר ביכולתו להביע את קשרי ההיסק הלוגיים בין טענות שאין אפשרות להביע באמצעות תחשיב הפסוקים. למשל, ניתן להראות באמצעותו כי הטיעון הבא הוא תקף:
- סוקרטס הוא פילוסוף.
- יש לפחות פילוסוף אחד.
בתחשיב הפרדיקטים הכמתים מופיעים כחלק מן המבנה הפנימי של הטענה, ובאמצעות כך ניתן כעת לנסח בו טענות שיש בהם כימות מרובה של מספר משתנים בעת ובעונה אחת. טכניקות אלו מעניקות ללוגיקה כוח להביע עובדות וקשרים שאינם ניתנים להבעה באמצעות תחשיב הפסוקים או בלוגיקה האריסטוטלית. למשל הוא מאפשר לתת תיאור של מושג המספר, של מושג האינסוף ושל מושג הגבול באנליזה המתמטית של פונקציות, שכן לשם הבעת מושגים אלו יש צורך בטענה מרובת כמתים מן הצורה "לכל ε קיים δ כך ש...". דוגמה פשוטה יחסית לאופן בו נעשה שימוש כזה בכמתים היא ההצרנה של הטענה "לכל אחד יש חבר", כאשר נציין את היחס בין חברים שוב כפרדיקט דו-מקומי, F:
דוגמאות נוספות ניתנות בערך תחשיב הפרדיקטים.
סמנטיקה של תחשיב הפרדיקטים
[עריכת קוד מקור | עריכה]הסמנטיקה של תחשיב הפרדיקטים מציעה פירושים, אשר במסגרתם בלבד ניתן ליחס לפסוקים ערך אמת. פירוש מסוים מעניק מובן לכל אחד מן הקבועים הלא לוגים (השמות והפרדיקטים) וקובע את תחום-הדיון אשר על פיו נקבע הטווח של הכמתים. לדוגמה:
- תחום הדיון D הוא קבוצת האובייקטים {דני, רני, יוני}
- השמות: a ו-b מייצגים את דני ורני בהתאמה
- הפרדיקטים: הפרדיקט החד-מקומי "חכם" מצוין על ידי P, ומקבל ערך אמת עבור האובייקטים {דני, רני}
- הפרדיקט הדו-מקומי "חבר של" מצוין על ידי R והקבוצה של האובייקטים המשויכת אליו היא הקבוצה המכילה את הזוג {<רני, יוני>}.
לא כל אובייקט בתחום דורש שיינתן לו שם. אולם צריך להיות ברור מן הסמנטיקה, עבור כל אובייקט וכל פרדיקט בתחום, האם הפרדיקט חל עליו או לא.
כעת ניתן להעריך את ערך האמת של הפסוקים הבאים בפירוש הנוכחי:
- מכיוון שבתחום הדיון שלנו לא לכל x הפרדיקט P מחזיר אמת, הפסוק אמיתי.
- או הפסוק השקול:
- מכיוון שבתחום הדיון שלנו אין אף אובייקט x כך שבזוג יחד עם דני (a) הפרדיקט R מחזיר אמת, הפסוק אמיתי.
- מכיוון שבתחום הדיון שלנו, עבור כל x ש-P חל עליו ניתן למצוא אובייקט y ש-P חל עליו, הפסוק אמיתי.
ענפי משנה נוספים של הלוגיקה בת ימינו
[עריכת קוד מקור | עריכה]לוגיקה מודלית
[עריכת קוד מקור | עריכה] ערך מורחב – לוגיקה מודלית
ערך מורחב – לוגיקה מודלית
לוגיקה מודָלית (modal logic) היא הרחבה של הלוגיקה הקלאסית, המאפשרת הגדרה פורמלית של ביטויים מודליים. ביטויים מודליים הם למשל כאלה המאפיינים את אמיתותם של משפטים, כגון "הכרחי" ו"אפשרי". לדוגמה, על פסוק כמו "יורד גשם", ניתן להפעיל את האופרטורים המודליים של ההכרח והאפשרות ולקבל "בהכרח יורד גשם" או "אפשרי שיורד גשם". הלוגיקה המודלית מציעה מספר מערכות אקסיומטיות בעלות תכונות שונות, והיא ניתנת להחלה במספר תחומים נוספים, למשל לשם תיאור מושגים דאונטיים (מושגי החובה וההיתר המוסרי, אותם ניתן להחיל על טענות הקובעות מה ראוי, מה אסור, ומה מותר) וטמפורליים (המאפשרת להביע את המובן הזמני של טענות כאופרטורים החלים על טענות לא-זמניות, וכך לייצג קשרי היסק לוגיים בין טענות אלו), וכן בתורת הידיעה (לוגיקה אפיסטמית) ובהסתברות.
לוגיקה אינטואיציוניסטית
[עריכת קוד מקור | עריכה] ערך מורחב – אינטואיציוניזם
ערך מורחב – אינטואיציוניזם
הלוגיקה האינטואיציוניסטית נובעת מעבודתו של המתמטיקאי לויצן אגברטוס יאן בראואר. היא אינה מכירה בחוק השלישי הנמנע (לפיו כל טענה היא אמיתית או שקרית, ללא חלופה אפשרית אחרת), ולפיכך היא אינה מאפשרת הוכחה בדרך השלילה. אקסיומת הבחירה של תורת הקבוצות נדחית אף היא. הלוגיקה האינטואיציוניסטית נוסחה באופן פורמלי על ידי ארנד הייטינג וארט בישופ, וקיבלה את התורה הסמנטית שלה מאת סול קריפקי.
לוגיקה עמומה
[עריכת קוד מקור | עריכה] ערך מורחב – לוגיקה עמומה
ערך מורחב – לוגיקה עמומה
לוגיקה עמומה, או לוגיקה מעורפלת (באנגלית: Fuzzy Logic), הוא שם כללי לתורות לוגיות המנסות להחיל את עקרונות החשיבה הרציונלית על תחומים שבהם נראה כי שני חוקי היסוד של הלוגיקה הקלאסית אינם מתאימים. בעיקר מדובר על תחומים שבהם יש צורך להתבסס על הערכות סובייקטיביות או רב-משמעיות (בתחומים הקשורים למדעי החברה או לכלכלה, כמו שיווק למשל).
ראו גם
[עריכת קוד מקור | עריכה]לקריאה נוספת
[עריכת קוד מקור | עריכה]- אלפרד טרסקי, מבוא ללוגיקה ולמיתודולוגיה של המדעים הדידוקטיביים, תרגם: יהושע בר-הלל בהשתתפות אי"י פוזננסקי, ירושלים: מוסד וויצמן, 1956
- יהושע בר-הלל, הגיון לשון ושיטה - מסות בפילוסופיה של הלוגיקה, של הלשון ושל המדע, תל אביב: ספרית פועלים, 1970
- שמואל הוגו ברגמן, מבוא לתורת ההיגיון - המדע העיוני של הסדר, ירושלים: מוסד ביאליק, 1975
- אירוינג מ. קופי, מבוא ללוגיקה, תרגום: חנן רותם, עריכה: מרסלו דסקל, תל אביב: יחדיו, 1977
- ענת בילצקי, מהי לוגיקה?, סדרת אוניברסיטה משודרת, בהוצאת משרד הביטחון – ההוצאה לאור, 2002
- יקיר לוין, יסודות תורת ההגיון: פרקי מבוא בדגש פילוסופי, ירושלים: הוצאת אקדמון, 1999
- ג'יימס אורמסון (עורך), הערכים: לוגיקה, אינדוקציה, דדוקציה, האנציקלופדיה לפילוסופיה מערבית, תל אביב: הוצאת רסלינג, 2007
- רמי ישראל, מבוא ללוגיקה (3 כרכים), רעננה: האוניברסיטה הפתוחה, תשע"א 2011
- רמי ישראל, שער ללוגיקה, רעננה: האוניברסיטה הפתוחה, 2022
קישורים חיצוניים
[עריכת קוד מקור | עריכה]- ד. ג'. או'קונור, תורת ההגיון, באנציקלופדיה לפילוסופיה מערבית
- סטיוארט שפירו, לוגיקה קלאסית, באנציקלופדיה לפילוסופיה של סטנפורד (באנגלית)
- קורס מקוון של אוניברסיטת אוקספורד, "מבוא ללוגיקה", באתר אוניברסיטת אוקספורד (באנגלית)
- לוגיקה, באתר אנציקלופדיה בריטניקה (באנגלית)
 לוגיקה, דף שער בספרייה הלאומית
לוגיקה, דף שער בספרייה הלאומית- לוגיקה, באתר MathWorld (באנגלית)
הערות שוליים
[עריכת קוד מקור | עריכה]- ^ מלשון צורה, להעניק צורה או ניסוח לוגי





































