This project aims to explore several variations of Thomas Schelling's (1969-71) work on residential segregation.

The following are notable features of this project:

• Three variations of simulation dynamics to choose from:
  • Liquid dynamics allow happy agents to move in addition to unhappy ones. This allows the simulation to execute continuously for as long as desired. See Vinković and Kirman (2006) for a discussion and Hatna and Benenson (2012) for the implementation this project uses.
  • Solid dynamics mirror those in Schelling's two-dimensional model. See one of his original papers (such as 1971) for a full discussion.
  • Swap dynamics eliminate the concept of vacancies and allow unhappy agents to swap with each other directly. See Rogers (2011) for a discussion on the merits of such a simplification and Zhang (2004, 2009) for an example of its use.
• Simulation configuration options such as boundary conditions, neighborhood size, and how often happy agents may relocate.
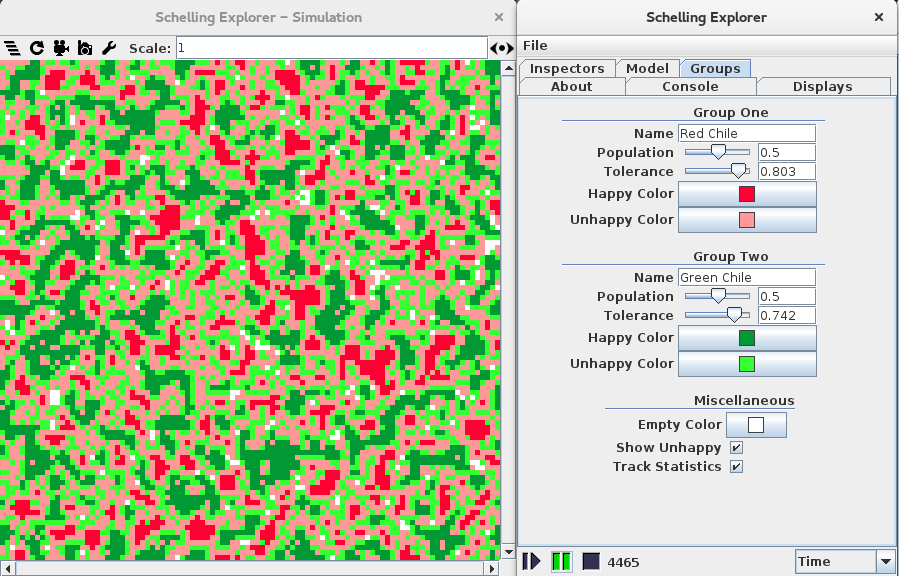
• Group configuration options such as color, tolerance, and population size.
• Statistics tracking and charting for both the interface density (a measure of the connection between agents of different groups) and the percentage of agents who are unhappy.

This project was written for Java 1.8 and uses Gradle as its build system. The excellent simulation toolkit MASON is used to provide the agent based modeling facilities as well as most of the widgets that comprise the user interface. Finally, this project requires JFreeChart with the iText PDF library for charting.

Please note that when building this project only MASON needs to be installed manually. This can be done using the requisite commands for Maven or Ivy depending on preference.

An example of this project in action is shown below and based on a typical New Mexican quandry: red or green?

This project is released under the Apache 2.0 license as specified in License.txt.

1. Hatna, E. and Benenson, I. (2012). The schelling model of ethnic residential dynamics: beyond the integrated-segregated dichotomy of patterns. Journal of Artificial Societies and Social Simulation, 15(1).
2. Rogers, T. and McKane, A.J. (2011). A unified framework for Schelling's model of segregation. Journal of Statistical Mechanics: Theory and Experiment.
3. Schelling, T. (1971). Dynamic models of segregation. Journal of Mathematical Sociology, 1(2), 143-186.
4. Vinković, D. and Kirman, A. (2006). A physical analogue of the Schelling model. Proceedings of the National Academy of Sciences of the United States of America, 103(51).
5. Zhang, J. (2004). A dynamic model of residential segregation. Journal of Mathematical Sociology, 28(3).