This project focuses on the evaluation of 4 different numerical methods based on the Finite Difference (FD) approach, the first 2 are explicit methods and the rest are implicit ones, and they are listed respectively, the DuFort-Frankel and Richardson methods, the Laasonen and Crank-Nicholson methods, in order to compute the solution of the 1D heat conduction equation with specified BCs and ICs, using C++ Object Oriented Programming (OOP).

The heat conduction equation is a parabolic, linear and constant coefficients partial differential equation, consequently, according to the literature some of the numerical methods that will be investigated will lead to accurate results compared to the exact solution, and some will have restrictions on stability and consistency which will affect the solution convergence, and these restrictions are imposed on the spatial and time domains.

The partial differential equation in hand is the unsteady 1D heat conduction equation, also known as the 1D diffusion model equation, in the Cartesian coordinates is shown below:

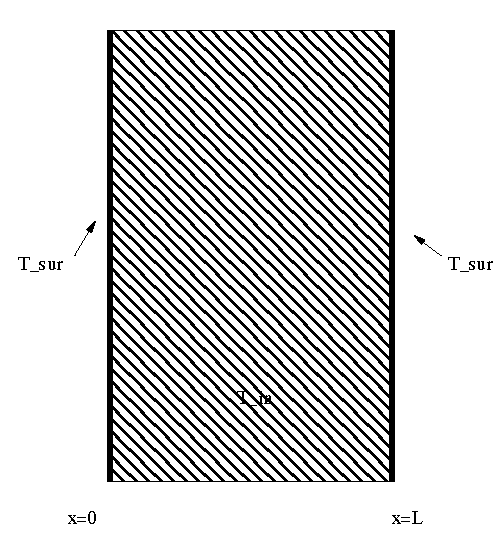
This PDE is the simplest parabolic equation, it is used to study the temperature distribution due to conduction heat transfer at a time t and location x resulting from an initial temperature distribution, in a wall composed of nickel steel (40% Ni) illustrated in figure below, with the following properties that will be used throughout the whole project:

• Diffusivity, D = 93 cm^2/hr,
• Thickness, L = 31 cm,
• Uniform Initial Temperature, T_in = 38 °C,
• Boundary Conditions, T_sur = 149 °C.

The exact analytical solution of this problem is represented by the following equation:

The methods that will be used are all based on Finite-differences approach which are derived from Taylor Series expansion.

A numerical method is said to be convergent if both stability and consistency of a finite difference scheme are satisfied, that is the numerical solution will converge to the exact solution of a linear PDE, and this is known as the Lax Equivalence Theorem, that can be expressed as in the following equation:

Consistency + Stability --> Convergence

This theorem does not hold for nonlinear PDEs, for instance the Navier–Stokes equations. Nevertheless, it does provide with the insight that satisfying these 2 criteria is important for developing convergent finite difference schemes.

The 4 methods implemented for the numerical solution of this problem are based on the most commonly used finite difference formulas, and they are divided in 2 categories, as below:

• Explicit Schemes:

  • DuFort-Frankel
  • Richardson

• Implicit Schemes:

  • Laasonen
  • Crank-Nicholson

The final formulation of this method is written as:

Applying the Von Neumann Analysis, this method turns out to be Unconditionally Stable, then in other words, the DuFort-Frankel method possess the same stability property as the Implicit Schemes. Also, this scheme is conditionally consistent, therefore an imposed condition on the grid and time domains is expressed as:

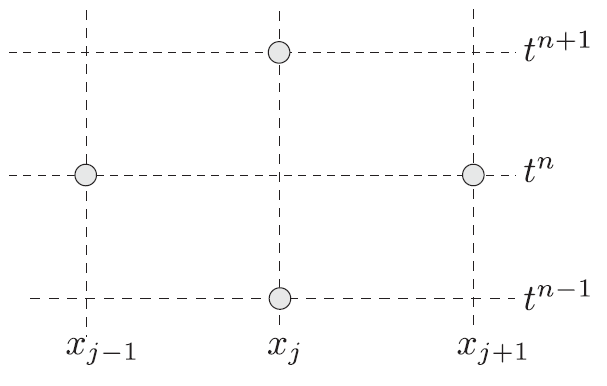
Moreover, this method represents a multistep method, the computational stencil is shown in the figure below.

Since as the formulation and stencil indicates, this method requires 2 sets of initial conditions to start the solution. The unknown variable at the next time step (n + 1) will require the values at time step (n) and (n - 1). In our case, one set of initial conditions (T_in) is specified, hence the second set will be calculated using the FTCS (Forward Time Centered Space) method, and the accuracy of the solution provided by the DuFort-Frankel method is affected by the accuracy of the starter solution that will be imposed by the FTCS method. The final formulation of the FTCS method is written as:

Applying the Von Neumann Analysis, for this method to be stable we should satisfy the following CFL condition:

The resulting equation for this method is represented below:

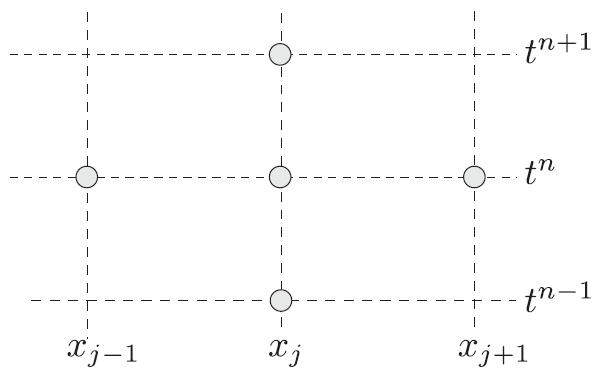
Richardson method is also a multistep scheme, the computational stencil is shown in the figure below. Like DuFort-Frankel, this method requires 2 sets of initial conditions, hence the FTCS will also be used in this case to calculate the second set of initial conditions.

Now for the stability, this method is found to be unconditionally unstable using Von Neumann Analysis. Thus, this method is of no practical use.

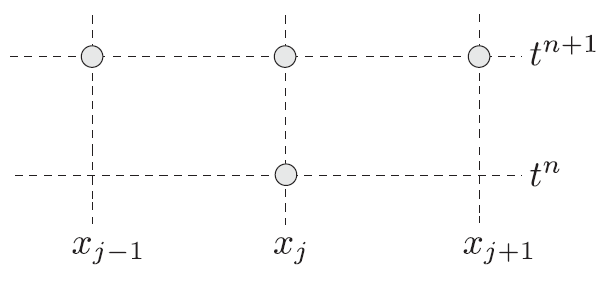
Also known as the Simple Implicit or Laasonen Implicit method. It is actually the FTCS method but in the implicit formulation. The final formulation of this method is the following:

The computational stencil for this method is shown in figure below.

Now, to solve this equation, it is necessary to consider all the gird points of the system, and their corresponding equations, which will lead to a system of linear algebraic equations represented by:

Thomas Algorithm, also known as Tridiagonal Matrix Algorithm (TDMA) is a very efficient solver for this type of matrices. This solver will be used to get the solution at the next time step, thus at each time step the system of linear equations will be solved using TDMA to reach the time t required for the solution.

Next, for the consistency of this method, using Taylor Series expansion for each term, this method turns out to be consistent. And for the stability analysis, this method is unconditionally stable for all values of time step (Delta_t) and grid spacing (Delta_x).

The final formulation of Crank-Nicholson is illustrated below:

The computational stencil for this method is shown in figure below.

This method, results in a tridiagonal system of equations which can also be solved as the Laasonen method using TDMA at every time step to obtain the solution at the required time.

For the consistency, using Taylor series expansion, this method is found to be consistent while having a truncation error of O(Delta_t^2, Delta_x^2). Thus, Crank-Nicholson is a considerable improvement over the Laasonen method, that is first order accurate in time.

For the stability properties of this method, using Von Neumann Analysis, the method is said to be unconditionally stable. However, the drawback of this method is that for large values of (D Delta_t)/(Delta x^2) and mainly for large (Delta_t), leads to oscillations of the solution, but the latter remains always bounded.

The provided source code was tested to run using C++17 and above using both Linux (Ubuntu or Debian) and Windows operating systems.

The following set-up is only adopted for Ubuntu or Debian Linux operating systems.

The GNU Compiler Collection (or GCC) includes front ends for C, C++, Objective-C, Fortran, Ada, Go, and D, as well as libraries for these languages (libstdc++,...). GCC was originally written as the compiler for the GNU operating system. The GNU system was developed to be 100% free software.

To install GNU C/C++ compiler included in GCC and its related tools, first open your terminal, and type the following commands in order to update and upgrade your packages list:

sudo apt-get update
sudo apt-get upgrade

Next, to install gcc, g++, make, etc. packages, type the commands:

sudo apt-get install build-essential
sudo apt-get install gdb            # To install the GNU Debugger (GDB) debugger
sudo apt-get install manpages-dev   # To install the manual pages about using GNU/Linux for development

Finally, to validate that the GCC compiler and GDB debugger are installed successfully, and to verify/display the installation version along with the directory location of the compiler, run the commands:

whereis gcc
gcc --version # or g++ --version
gdb --version

MinGW ("Minimalist GNU for Windows") formerly Mingw32, is a native port of the GNU Compiler Collection (GCC) to Windows operating system, with freely distributable import libraries and header files for building native Windows applications. Most languages supported by GCC are supported on the MinGW port as well. These include C, C++, Objective-C, Objective-C++, Fortran, and Ada. The GCC runtime libraries are used (libstdc++ for C++, libgfortran for Fortran, etc.). Although programs produced under MinGW are 32-bit executables, they can be used both in 32 and 64-bit versions of Windows.

On the other hand, Mingw-w64 is a fork of Mingw32, that can generate 32 bit and 64-bit executables.

To run C/C++ compiler on Windows, follow the next steps:

1. Install first Mingw-w64 Online Installer from the SourceForge website:

   • Run the installer.
   • For Architecture select x86_64 and then select Next.
   • On the Installation Folder page, use the default installation folder. Copy the location as you will need it later.
   • Select Next to start the installation.

2. Add the path to your Mingw-w64 bin folder to the Windows PATH environment variable by using the following steps:

   • In the Windows search bar, type "settings" to open your Windows Settings.
   • Search for "Edit environment variables for your account".
   • Choose the Path variable in the System variables and then select Edit.
   • Select New and add the Mingw-w64 bin destination folder path to the system path.
   • Select OK to save the updated PATH.

3. Check your Mingw-w64 installation:

   • To check that your Mingw-w64 tools are correctly installed and available, open a new Command Prompt (cmd) and type:

     gcc --version &:: or g++ --version
     gdb --version

For free text and source code editors, I recommend using:

• Notepadqq
• Visual Studio Code

• Notepad++
• Visual Studio Code

Open your terminal, then navigate to your source code directory. Next, run the following commands to compile the C++ source code:

mkdir Solution   # Create a new directory for the solution 
g++ main.cpp vector.cpp -o Solution/1D_Heat_Equation_Program.out   # To compile the Non OOP source code
g++ main.cpp explicit.cpp implicit.cpp analysis.cpp vector.cpp -o Solution/1D_Heat_Equation_Program.out   # To compile the OOP source code
cd Solution   # Navigate to the solution directory
./1D_Heat_Equation_Program.out   # To run the 1D Heat Equation program

Open Command Prompt (cmd), then navigate to your source code directory. Next, run the following commands to compile the C++ source code:

mkdir Solution   &:: Create a new directory for the solution 
g++ main.cpp vector.cpp -o Solution/1D_Heat_Equation_Program.exe   &:: To compile the Non OOP source code
g++ main.cpp explicit.cpp implicit.cpp analysis.cpp vector.cpp -o Solution/1D_Heat_Equation_Program.exe   &:: To compile the OOP source code
cd Solution   &:: Navigate to the solution directory
1D_Heat_Equation_Program.exe   &:: To run the 1D Heat Equation program

This project was part of the Master of Science (MSc) degree in Aerospace Computational Engineering at Cranfield University for the academic year 2019/2020, where the main and only contributors are:

• Sevan Retif (Student at Cranfield University UK, No GitHub profile & Email: [email protected])
• Elias Farah (Student at Cranfield University UK, GitHub: @Eliasfarah0 & Email: [email protected])