A collection of solvers for many puzzles that I've written over the years. I've found that solving puzzles is a great way to teach myself new techniques from the combinatorial optimization field, and in fact I have used many of them in my actual job as a software engineer.

For extra motivation of why should anyone spend time programming puzzles, I recommend the article "Are Toy Problems Useful?", written by Donald Knuth (and reprinted in Selected Papers on Computer Science).

Almost all puzzles here can be played online on the wonderful site janko.

The methods used to solve the puzzles so far:

• Exact cover: an implementation using the Dancing Links algorithm.
• Color-controlled covering: an extension of Exact Cover where items can be assigned colors.
• Constraint programming: A small library I wrote, allowing for arbitrary constraints, and falling back to backtracking when no information can be extracted by manipulating the constraints.
• Mixed integer programming: Programming MIP from scratch is hard, so instead I wrote an easy-to-use C++ frontend to the external library SCIP.
• Human-based reasoning: An expert system encoding rules as a human would solve it.

Rules:

• Place light bulbs on the board in a way every cell in the board gets illuminated.
• Each light bulb shines its entire row and column, unless blocked by a black cell.
• No light bulbs can shine another light bulb.
• Cells numbered indicate the number of adjacent light bulbs (diagonals doesn't count).

Rules:

• Each row and column must have the same number of 0 and 1.
• You can't place more than two of the same number adjacent to each other.
• All rows and columns must be unique.

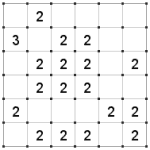
Rules:

• Every row, column and group must have the same number of stars (the number is given, usually one or two).
• Stars can't touch each other, not even on diagonals.

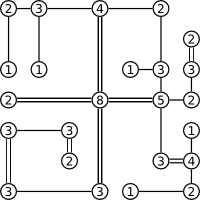
Rules:

• Connect all islands with bridges.
• Bridges must be horizontal or vertical.
• Bridges can't cross each other.
• Islands can be connected by one or two bridges.
• The number on the island is the number of bridges connected to it.
• All islands must be connected in a single group.

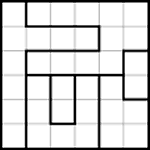
Rules:

• Draw lines between dots forming a single loop.
• Numbered cells must have exactly that much lines on their edges.

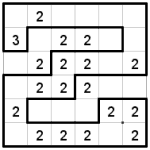
Rules:

• Draw white islands in the grid.
• Each island much have exactly one number.
• The number indicates the size of the island.
• Islands are 4-connected and must not touch other islands.
• The river around the islands must be 4-connected in a single group.
• There can be no 2x2 black blocks in the river.

Rules:

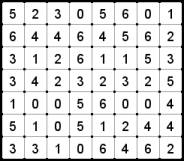
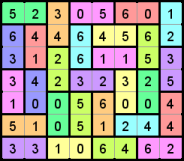
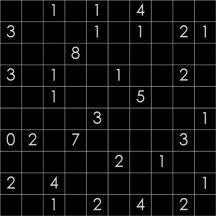
• Each row, column and group must have all numbers from 1 to 9 (or less for smaller puzzles).

Rules:

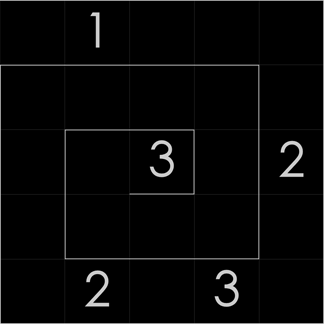
• Split the board into unique dominos (tiles which are 1x2 or 2x1).

Rules:

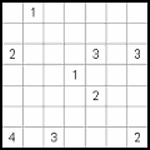
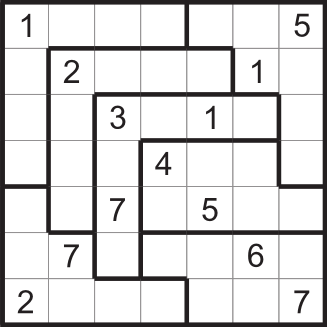
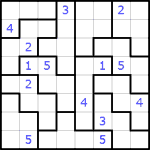
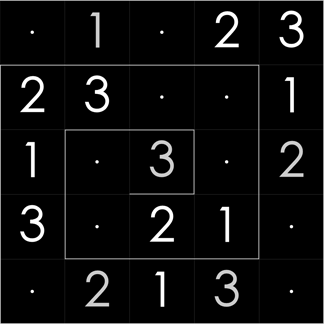
• Each group of size n must have all numbers from 1 to n.
• Numbers can't touch each other, not even on diagonal.

Rules:

• Every seed must have branches whose sum length is equal to the number.
• Branches only grow in horizontal and vertical.
• Every cell must have a branch.

Rules:

• Place numbers from 1 to n on the board.
• The first number in the snail must be 1, the last must be n.
• The number along the snail must follow the sequence 1 to n, repeating as needed.
• Each row and each column must have exactly one number from 1 to n.

Rules:

• Place words in a 6x3 grid of letters.
• The words must appear in the grid as a noncrossing chess king path.