Implementaton of Q.V. Le, and T. Mikolov's Paragraph Vector Distributed Memory algorithm [1]. Obtain a summary vector for a document of any size for document retrieval, sentiment analysis, and other NLP tasks.
The idea behind PVDM is to obtain summary vectors for paragraphs, sentences, documents, etc. by using them as a crutch during a missing word task. Word2vec[2] offers a similar setup where a word window with an omitted central word is used to train word vectors for the other words in the window such that they predict the middle word. In this instance predicting the middle word is done using the surrouding words along with a special memory word, the paragraph vector. During training all words plus this paragraph vector are backproped to, and thus will capture some of the regression 'needs' of the task.
To deal with such a large prediction task (over 30k, 100k, or more words), the authors use clever sparse schemes. Hierachical Softmax for instance, is a method that records the position of the words in a tree (in this case a Huffman tree built using their occurences in the training data, or in some large corpus) and uses their corresponding Huffman binary codes for regression. The codes are used as follows: by only calling the columns of a giant matrix that corresponds to each branching point in the tree, it is possible to train the neighbor words to force the neural net to activate in such a way to reproduce this code, which in turns would mean taking all the correct turns as we travel down the tree to the target word. An excellent overview of this technique is given here.
[1] Quoc V. Le, and Tomas Mikolov, ``Distributed Representations of Sentences and Documents ICML", 2014 [1].
[2] Tomas Mikolov, Kai Chen, Greg Corrado, and Jeffrey Dean, ``Efficient Estimation of Word Representations in Vector Space. In Proceedings of Workshop at ICLR", 2013.
This code is based off gensim's word2vec code, and thus ressembles its implementation.
We start off by loading the library:
from word2vec_extended import LineCorpus
from pvdm import PVDM, ParagraphThe LineCorpus is a wrapper around a reader for a text file with a new sentence on each line:
trees = utils.import_tree_corpus("sentiment_data/other_data/train.txt")
labels_hash = trees.labels()
tree_export_path = "sentiment_data/all_lines.txt"
tree_corpus = LineCorpus(tree_export_path, filter_lines = False)
# filter lines removes lines with crazy non alphanumerical charactersWe can now initialize the model:
pvdm = PVDM(
concatenate = True,
random_window = True,
workers = 8,
window = 8,
batchsize = 1000,
paragraph_size=400,
decay = False,
size = 400,
alpha=0.035,
symmetric_window =False,
self_predict = False)As in [1] we note that it is possible to concatenate the words in the window with the paragraph vector, or to instead sum the words together and concatenate this sum with the paragraph. This is controlled via the concatenate parameter.
To evaluate this model on test data we need to be able to freeze the parameters of the model (vocabulary, regression parameters for the hierachical softmax, etc...):
We create a special indexing scheme for the new paragraphs, along with a matrix to store their vectors:
test_trees = utils.import_tree_corpus("sentiment_data/other_data/test.txt")
index2paragraph_test = [tree.to_lines()[0] for tree in test_trees]
test_paragraph_vocab = {}
for line in index2paragraph_test:
p = Paragraph()
p.index = len(test_paragraph_vocab)
test_paragraph_vocab[line]= p
paragraphs = (np.random.randn(len(test_paragraph_vocab), pvdm.paragraph_size) * 1.0 / pvdm.paragraph_size) .astype(dtype=np.float32)Re-optimize the paragraph vectors for training set by passing the matrix and the indexing scheme, and preventing updates to the other parameters by passing paragraphs_only as True:
alpha = 0.035
epochs = 300
retraining_errors = []
try:
for epoch in range(epochs):
pvdm.alpha = max(0.0001, alpha * (1 - 1.0 * epoch / (epochs-1)))
words, error = pvdm.train(tree_corpus, paragraphs_only=True)
print("Epoch %d: error %.3f, alpha = %.5f" % (epoch, error, pvdm.alpha))
if error < 5:
break
if epoch > 0 and error > errors[-1]:
retraining_errors.append(error)
else:
retraining_errors.append(error)
except KeyboardInterrupt:
print("Epoch %d: error %.3f, alpha = %.5f" % (epoch, error, pvdm.alpha))Epoch 0: error 259231.325, alpha = 0.03500
Epoch 1: error 149707.214, alpha = 0.03488
Epoch 2: error 130148.975, alpha = 0.03477
Epoch 3: error 120242.958, alpha = 0.03465
...
Epoch 54: error 52776.152, alpha = 0.02868
Epoch 55: error 52448.319, alpha = 0.02856
Epoch 56: error 52331.296, alpha = 0.02844
Epoch 57: error 52331.296, alpha = 0.02833
Optimize the paragraph vectors for test set:
alpha = 0.035
epochs = 300
test_errors = []
try:
for epoch in range(epochs):
pvdm.alpha = max(0.0001, alpha * (1 - 1.0 * epoch / (epochs-1)))
words, error = pvdm.train((sentence.split() for sentence in index2paragraph_test), paragraphs=paragraphs, vocab = test_paragraph_vocab, paragraphs_only=True)
print("Epoch %d: error %.3f, alpha = %.5f" % (epoch, error, pvdm.alpha))
if error < 1:
break
if epoch > 0 and error > errors[-1]:
test_errors.append(error)
else:
test_errors.append(error)
except KeyboardInterrupt:
print("Epoch %d: error %.3f, alpha = %.5f" % (epoch, error, pvdm.alpha))Several technical points in the paper provide interesting variants of the model that affect parts of the code:
In the paper it was ambiguous whether the word windows predict the center word or the word at the extremity (Word2vec predicts the center word, but the language and figures in [1] indicate the end word instead). The parameter symmetric_window controls whether to predict the center word or not.
Next we consider the sampling strategy. Should we see each word window in a sentence even if it is longer than all the others, and thus would be trained much more than other examples ? Or should we instead sample each window from each example equally ? Again we leave it up to the user to decide which behavior to choose with the paramer random_window.
Ultimately we are not looking to build another Word2vec, so should we allow the predicted word to predict itself, since we are only looking to train paragraph vectors (if we did care about the words then letting the target word predict itself may lead to a degenerate solution). This behavior is controlled by the parameter self_predict. We recommend to set this to False.
To get the system working provide it with a vocabulary source:
pvdm.build_vocab(sentences = tree_corpus, oov_word = True)Then train it:
alpha = 0.035
epochs = 130
errors = []
try:
for epoch in range(epochs):
pvdm.alpha = max(0.0001, alpha * (1 - 1.0 * epoch / (epochs-1)))
words, error = pvdm.train(tree_corpus, paragraphs_only = False)
print("Epoch %d: error %.3f, alpha = %.5f" % (epoch, error, pvdm.alpha))
if error < 5:
break
if epoch > 0 and error > errors[-1]:
errors.append(error)
else:
errors.append(error)
except KeyboardInterrupt:
print("Epoch %d: error %.3f, alpha = %.5f" % (epoch, error, pvdm.alpha))Epoch 0: error 12238564.014, alpha = 0.03500
Epoch 1: error 9035877.274, alpha = 0.03473
Epoch 2: error 7462139.332, alpha = 0.03446
Epoch 3: error 6378156.541, alpha = 0.03419
Epoch 4: error 5566759.061, alpha = 0.03391
Epoch 5: error 4954506.754, alpha = 0.03364
Epoch 6: error 4433725.362, alpha = 0.03337
...
Epoch 127: error 907829.069, alpha = 0.00054
Epoch 128: error 1058162.380, alpha = 0.00027
Epoch 129: error 1215409.188, alpha = 0.00010
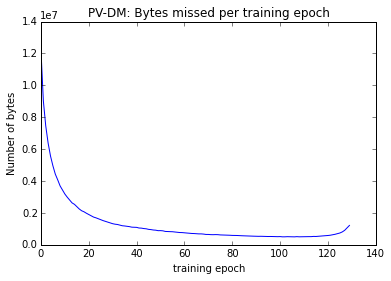
We find that the error drops rapidly, and then re-increases (this is probably due to the randomness of the sampling strategy, and the batch size):
We can now ask ourselves how the paragraphs are embedded:
Using T-SNE to get 2D projection of paragraphs:
# the trees variable is a special array of tree-like objects
# that capture the structure of the Stanford Sentiment Treebank
# dataset, to simply get the full sentences we grab the largest
# chunk of each tree:
full_lines = [tree.to_lines()[0] for tree in trees]
# convert these to indices from the matrices in the PVDM:
para_indices = [pvdm.paragraph_vocab[line].index for line in full_lines]
# throws those into bh_sne, a T-SNE library for python:
X_2dpara = bh_sne(pvdm.synparagraph[para_indices].astype('float64'))
min_visible = 10
max_visible = 50
para_labels = full_lines
para_colors = [labels_hash[label] for label in para_labels[min_visible:min_visible+max_visible]]
axes = plt.axes([0, 1, 3, 3])
axes.scatter(X_2dpara[min_visible:min_visible+max_visible,0], X_2dpara[min_visible:min_visible+max_visible, 1], marker = 'o', cmap=plt.cm.seismic, s = 80)
for label, x, y in zip(para_labels[min_visible:min_visible+max_visible], X_2dpara[min_visible:min_visible+max_visible, 0], X_2dpara[min_visible:min_visible+max_visible, 1]):
plt.annotate(
label,
xy = (x, y), xytext = (-8, -3),
textcoords = 'offset points', ha = 'right', va = 'bottom',
bbox = None,
arrowprops = None)#dict(arrowstyle = '->', connectionstyle = 'arc3,rad=0'))One of the goals of this implementation was to reproduce the results in [1] concerning sentiment analysis tasks over the Stanford Sentiment Treebank. To do this we need to import the test dataset, train a classifier, and benchmark:
labels = [labels_hash[label] for label in pvdm.index2paragraph]Here we have multiple options. We can construct a simple regressor ourselves, or use an off-the-shelf one from Sk-learn (The logistic regressor we built is not provided yet with this package).
Custom Logistic Regression classifier:
reg = LogisticRegression(embedding_size=pvdm.layer1_size, target_size=5, weight_decay=True, alpha = 1.5, criterion = 'kl_divergence')
errs = reg.sgd_fit(pvdm.synparagraph, labels, flush_output=True, verbose = True, max_iter = 400, batchsize=400)
#reg.fit_until_convergence(pvdm.synparagraph[para_indices], labels, verbose =True, flush_output=True);
Epoch 38: mean kl_divergence 1.249, 81795 / 159271 correct, alpha = 1.357, remaining tries 3
reg.alpha.set_value(np.float32(0.2))
errs = reg.sgd_fit(pvdm.synparagraph, labels, flush_output=True, verbose = True, max_iter = 400, batchsize=400)
Epoch 59: mean kl_divergence 1.282, 81454 / 159271 correct, alpha = 0.170, remaining tries 3Sk-learn Logistic Regression classifier: (too slow for full dataset)
# too slow:
#sk_reg = skLogisticRegression(tol=0.0000001)
#sk_reg.fit(pvdm.synparagraph[para_indices], labels);Classification report for custom Logistic Regressor:
print(classification_report(labels, reg.predict(pvdm.synparagraph), labels=[0,1,2,3,4], target_names=["--", "-", "", "+", "++"])) precision recall f1-score support
-- 0.07 0.00 0.00 7237
- 0.24 0.01 0.01 27714
0.52 0.98 0.68 81638
+ 0.39 0.05 0.09 33361
++ 0.21 0.01 0.01 9321
avg / total 0.40 0.51 0.37 159271
Classification report for Sk-Learn Logistic Regression:
print(classification_report(labels, sk_reg.predict(pvdm.synparagraph), labels=[0,1,2,3,4], target_names=["--", "-", "", "+", "++"])) precision recall f1-score support
-- 0.30 0.02 0.04 1092
- 0.32 0.46 0.38 2218
0.34 0.12 0.17 1624
+ 0.32 0.61 0.42 2322
++ 0.37 0.08 0.13 1288
avg / total 0.33 0.32 0.27 8544
There appears to be an issue with overfitting in the Sk-learn version which we tried to avert with some early stopping / etc.. Nothing too fancy, but some cooking happens here. As we can see we get about 51% recall over all phrases (sentences and sub-sentences [phrases and words]).
We may ask, but how sharp are these results ? i.e. is the embedding forcing these hyperplanes to exist for classification, or can we throw it back in the oven for a few more hours and crank some more goodness ? Well see for yourselves:
plt.matshow(reg.predict_proba(pvdm.synparagraph[20:60]), interpolation='nearest', cmap=plt.cm.Spectral)
plt.colorbar();So it's quite cooked.
Now it's time to throw it into the deep end with the test set (data it was not exposed to !).
Get the labels in a list:
test_labels_hash = test_trees.labels()
test_labels = [test_labels_hash[sentence] for sentence in index2paragraph_test]Get performance on the test set:
print(classification_report(test_labels, reg.predict(paragraphs), labels=[0,1,2,3,4], target_names=["--", "-", "", "+", "++"])) precision recall f1-score support
-- 0.00 0.00 0.00 279
- 0.00 0.00 0.00 633
0.18 1.00 0.30 389
+ 0.00 0.00 0.00 510
++ 0.00 0.00 0.00 399
avg / total 0.03 0.18 0.05 2210
The results are not as good as on the training set, expectedly, but not where we'd like them to be to reproduce [1]. Let us first note that there are only 2210 examples here, and all are full sentences. The other questions you may ask are, but were the vectors well trained ? etc... those are all good open questions, and they may help explain the discrepancy. Let's now focus on what works well here.
The embeddings capture useful information. One way of verifying that this process works is to find the nearest Eucledian neighbors for these guys.
First look for neighboring words (just as in Word2vec):
pvdm.most_similar("darkness")[('lameness', 0.7936276793479919),
('anti-virus', 0.7769980430603027),
('contributions', 0.7643187642097473),
('preaches', 0.7543584704399109),
('pinnacle', 0.7475813031196594),
('multiplex', 0.7469998598098755),
('art-conscious', 0.7468372583389282),
('dictates', 0.7405220866203308),
('witch', 0.7355045080184937),
('owed', 0.7308557033538818)]
Now look for neighboring paragraphs, note that "bad" here is treated as the paragraph "bad" which thus has a distinct vector from the word vector for "bad":
for label, score in pvdm.most_similar_paragraph("bad"):
print("%s - %.2f" % (label, score))
#print("prediction %d vs actual %d" % (reg.predict([pvdm.synparagraph[pvdm.paragraph_vocab[label].index]])[0], labels_hash[label]))
print()lot - 0.93
prediction 0 vs actual 2
down - 0.89
prediction 2 vs actual 2
car pileup - 0.88
prediction 2 vs actual 2
before - 0.87
prediction 2 vs actual 2
powerful - 0.84
prediction 1 vs actual 4
strong subject matter - 0.83
prediction 2 vs actual 2
bad sign - 0.82
prediction 2 vs actual 1
lot to be desired - 0.82
prediction 2 vs actual 1
bad bluescreen - 0.82
prediction 2 vs actual 0
bad boy weirdo role - 0.79
prediction 2 vs actual 2
Here we note that many of the returned paragraphs are very relevant to our query, and thus, at least in this small example, we can see that this technique can be very useful for optaining proximity of two phrases (paraphrasing for instance).