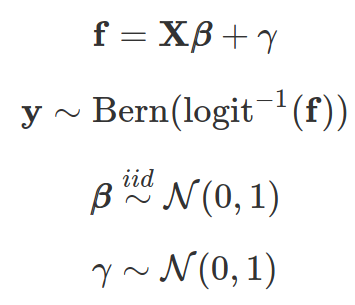JAX ADVI is a small library designed to do black-box variational inference using automatic differentiation variational inference (ADVI) using JAX. Specifically, it implements the variant proposed by Giordano et al. which allows the use of (approximate) second order methods, which can be more robust. You can read about the methodology on my blog.
To use this library, you'll need JAX. If you want to run the examples, you'll also need:
- Pandas
- Scikit-learn
- Matplotlib
- Pystan
To install, clone this repository and run python setup.py develop.
The key function is optimize_advi_mean_field. Here's a simple example of a logistic regression:
Model:
Code:
from jax_advi.advi import optimize_advi_mean_field
from jax import jit
from jax.scipy.stats import norm
from functools import partial
from jax.nn import log_sigmoid
# Define parameter shapes:
theta_shapes = {
'beta': (K),
'gamma': ()
}
# Define a function to calculate the log likelihood
def calculate_likelihood(theta, X, y):
logit_prob = X @ theta['beta'] + theta['gamma']
prob_pres = log_sigmoid(logit_prob)
prob_abs = log_sigmoid(-logit_prob)
return jnp.sum(y * prob_pres + (1 - y) * prob_abs)
# Define a function to calculate the log prior
def calculate_prior(theta):
beta_prior = jnp.sum(norm.logpdf(theta['beta']))
gamma_prior = jnp.sum(norm.logpdf(theta['gamma']))
return beta_prior + gamma_prior
# The partial application basically conditions on the data (not defined in this
# little snippet)
log_lik_fun = jit(partial(calculate_likelihood, X=X, y=y))
log_prior_fun = jit(calculate_prior)
# Call the optimisation function
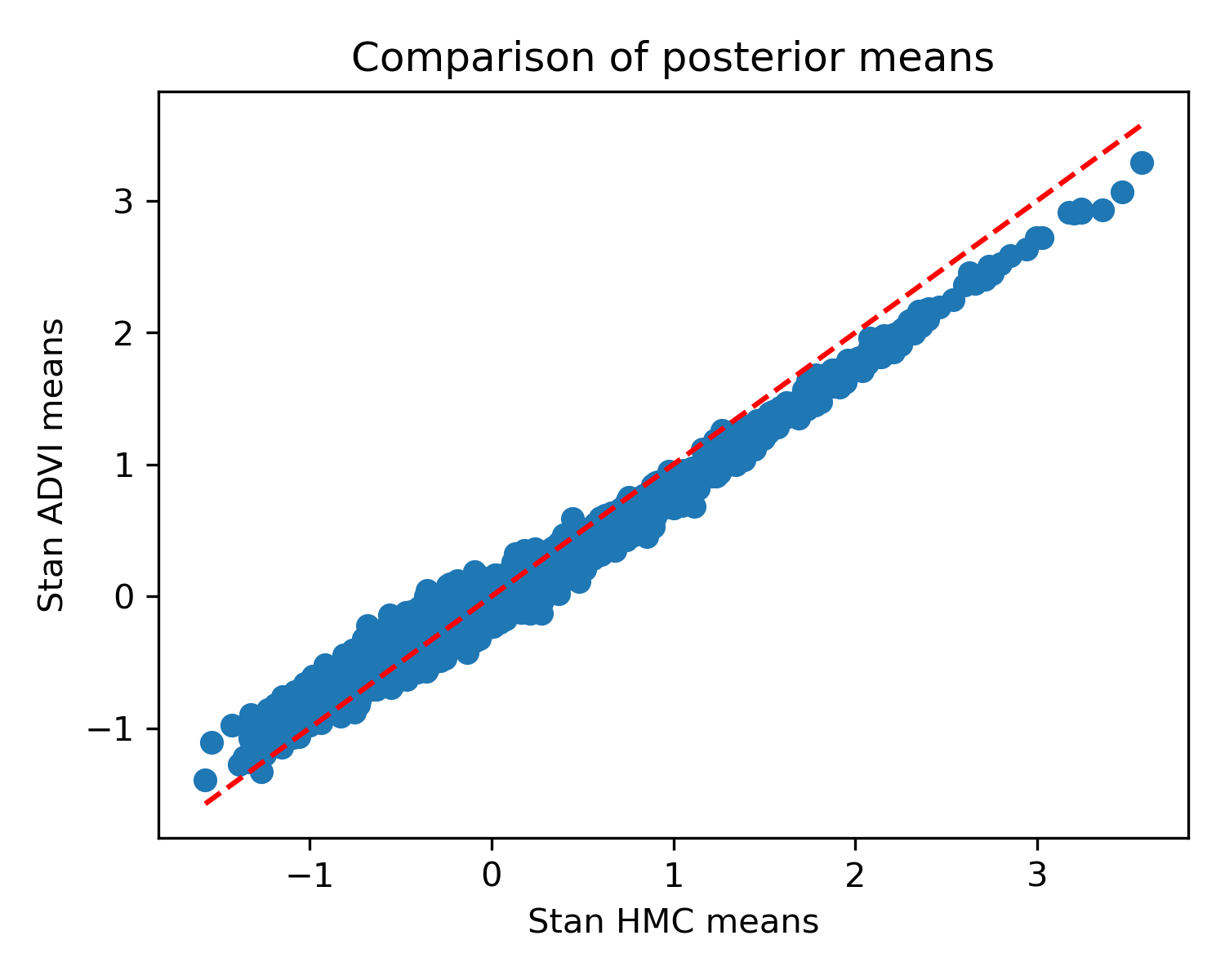
result = optimize_advi_mean_field(theta_shapes, log_prior_fun, log_lik_fun, n_draws=None)JAX ADVI should typically get the means right, but the variances may be off. For a full example comparing against Stan's HMC, see the example notebook. Here is a comparison for some toy data, taken from that example:
As promised, good means, less reliable standard deviations.
A more complex example is the following hierarchical model:
You can read a bit more about it in the blog post if you like. Here's what the code looks like:
Define shapes:
theta_shapes = {
'player_skills': (n_p),
'skill_prior_sd': ()
}Constrain the prior standard deviation to be positive:
from jax_advi.constraints import constrain_positive
theta_constraints = {
'skill_prior_sd': constrain_positive
}Define the log likelihood and prior:
from jax.scipy.stats import norm
from jax import jit
from jax.nn import log_sigmoid
import jax.numpy as jnp
@jit
def log_prior_fun(theta):
# Prior
skill_prior = jnp.sum(norm.logpdf(theta['player_skills'], 0., theta['skill_prior_sd']))
# hyperpriors
hyper_sd = norm.logpdf(theta['skill_prior_sd'])
return skill_prior + hyper_sd
def log_lik_fun(theta, winner_ids, loser_ids):
logit_probs = theta['player_skills'][winner_ids] - theta['player_skills'][loser_ids]
return jnp.sum(log_sigmoid(logit_probs))
from functools import partial
curried_lik = jit(partial(log_lik_fun, winner_ids=winner_ids, loser_ids=loser_ids))Finally, optimize:
result = optimize_advi_mean_field(
theta_shapes, log_prior_fun, curried_lik,
constrain_fun_dict=theta_constraints, verbose=True, M=100)You can run the example and compare it against Stan using the example notebook. Again, the means are good and the variances are a bit off:
The fit took 10s on my laptop with a GTX 2070, compared to 100 minutes in Stan, so you do get quite a speedup. It's also more accurate than Stan's ADVI, which gives the following means:
I hope you find this library useful. Please raise issues if anything doesn't work. Please note that this is still a new package and I wouldn't trusting it blindly yet. Its mean estimates seem reliable so far, but I recommend checking them against Stan's (or another MCMC framework) to be sure. If you find examples that break it, I'd be very interested to see them.