This is a Poisson 2D equation Python solver using FEM.
The main file is <PoissonSolver1D.py>

The Poisson eguation given as following:

-(a(x)u'(x))' = f(x) for all x belongs to I = (0,1)  
 a(x)u'(0) = k_0(u(0) - g_0)  
-a(x)u'(1) = k_1(u(1) - g_1) 

Which is Robin general boundry condition (BC).

If k_i = 0, this implies Neumann BC (in the following example in the code we use k_1 = 0).
While if k_i tends to infinity, this implies Dirichlet BC.
(also in the same example, we take k_0 = 10^6 which gives u(0) = g_0).

You can change the input functions a(x) and f(x) for a specific problem from the file <inputfuncs.py>

The input parameters k_i and g_i for i = {0,1} can be changed from the main file <PoissonSolver1D.py>.

kappa = [k_0, k_1]
g = [g_0 g_1]

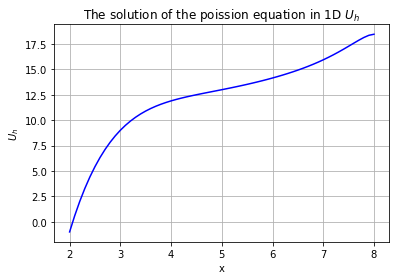
In the domain [2,8] for

k_0 = 10^6 (i.e. K_0 is very large which leads to u(2) = g_0), K_1 = 0 and g_0 = -1.  
with a(x) = 0.1*(5 - 0.6*x)
and f(x) = 0.03*(x-6)^4

i.e. the solved poisson equation is:

-((0.1*(5 - 0.6*x))u'(x))' = 0.03*(x-6)^4  for all x belongs to I = (2,8)  
 u(2) = -1,  (0.1*(5 - 0.6*x)u'(8) = 0

we have the approximated solution U_h:

Where the linear shape functions is:

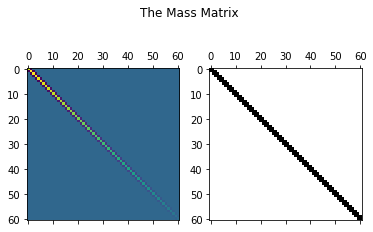
which gives the stiffness matrix:

Maged Shaban
magshaban[at]gmail.com