The mice package implements a method to deal with missing data. The package creates multiple imputations (replacement values) for multivariate missing data. The method is based on Fully Conditional Specification, where each incomplete variable is imputed by a separate model. The MICE algorithm can impute mixes of continuous, binary, unordered categorical and ordered categorical data. In addition, MICE can impute continuous two-level data, and maintain consistency between imputations by means of passive imputation. Many diagnostic plots are implemented to inspect the quality of the imputations.

The mice package can be installed from CRAN as follows:

install.packages("mice")

The latest version can be installed from GitHub as follows:

install.packages("devtools")
devtools::install_github(repo = "amices/mice")

library(mice, warn.conflicts = FALSE)

# show the missing data pattern
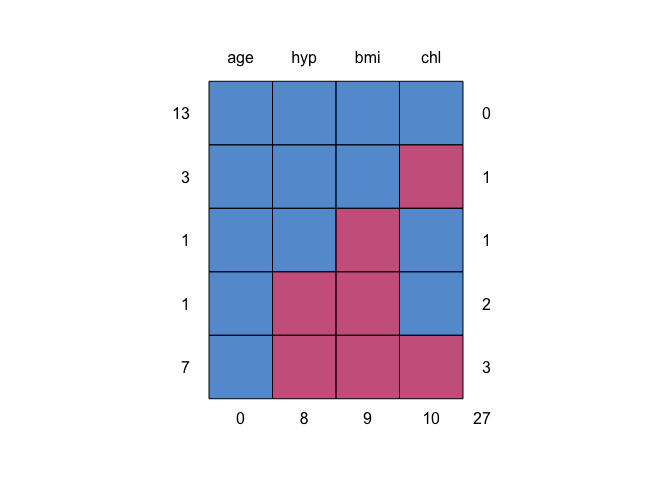
md.pattern(nhanes)

#>    age hyp bmi chl   
#> 13   1   1   1   1  0
#> 3    1   1   1   0  1
#> 1    1   1   0   1  1
#> 1    1   0   0   1  2
#> 7    1   0   0   0  3
#>      0   8   9  10 27

The table and the graph summarize where the missing data occur in the nhanes dataset.

# multiple impute the missing values
imp <- mice(nhanes, maxit = 2, m = 2, seed = 1)
#> 
#>  iter imp variable
#>   1   1  bmi  hyp  chl
#>   1   2  bmi  hyp  chl
#>   2   1  bmi  hyp  chl
#>   2   2  bmi  hyp  chl

# inspect quality of imputations
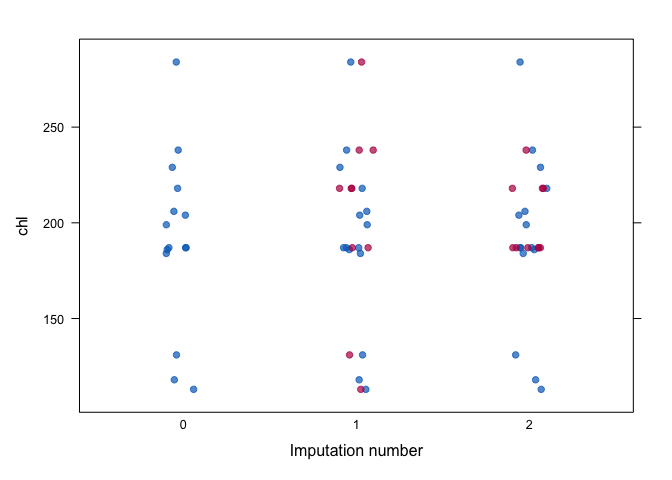
stripplot(imp, chl, pch = 19, xlab = "Imputation number")

In general, we would like the imputations to be plausible, i.e., values that could have been observed if they had not been missing.

# fit complete-data model
fit <- with(imp, lm(chl ~ age + bmi))

# pool and summarize the results
summary(pool(fit))
#>          term estimate std.error statistic    df p.value
#> 1 (Intercept)     9.08     73.09     0.124  4.50  0.9065
#> 2         age    35.23     17.46     2.017  1.36  0.2377
#> 3         bmi     4.69      1.94     2.417 15.25  0.0286

The complete-data is fit to each imputed dataset, and the results are combined to arrive at estimates that properly account for the missing data.

Version 3.0 represents a major update that implements the following features:

1. blocks: The main algorithm iterates over blocks. A block is simply a collection of variables. In the common MICE algorithm each block was equivalent to one variable, which - of course - is the default; The blocks argument allows mixing univariate imputation method multivariate imputation methods. The blocks feature bridges two seemingly disparate approaches, joint modeling and fully conditional specification, into one framework;

2. where: The where argument is a logical matrix of the same size of data that specifies which cells should be imputed. This opens up some new analytic possibilities;

3. Multivariate tests: There are new functions D1(), D2(), D3() and anova() that perform multivariate parameter tests on the repeated analysis from on multiply-imputed data;

4. formulas: The old form argument has been redesign and is now renamed to formulas. This provides an alternative way to specify imputation models that exploits the full power of R’s native formula’s.

5. Better integration with the tidyverse framework, especially for packages dplyr, tibble and broom;

6. Improved numerical algorithms for low-level imputation function. Better handling of duplicate variables.

7. Last but not least: A brand new edition AND online version of Flexible Imputation of Missing Data. Second Edition.

See MICE: Multivariate Imputation by Chained Equations for more resources.

I’ll be happy to take feedback and discuss suggestions. Please submit these through Github’s issues facility.

1. Van Buuren, S. (2018). Flexible Imputation of Missing Data. Second Edition.. Chapman & Hall/CRC. Boca Raton, FL.

1. Handling Missing Data in R with mice
2. Statistical Methods for combined data sets

1. Ad hoc methods and the MICE algorithm
2. Convergence and pooling
3. Inspecting how the observed data and missingness are related
4. Passive imputation and post-processing
5. Imputing multilevel data
6. Sensitivity analysis with mice
7. Generate missing values with ampute

1. Flexible Imputation of Missing Data. Second edition.

The cute mice sticker was designed by Jaden M. Walters. Thanks Jaden!

Please note that the mice project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.