Create, plot, and investigate Collatz sequences.

A Collatz sequence can start from any positive whole number (except 0). The next term is decided by the following rules:

1. If the previous term is even, the next term is half the previous term
2. If the previous term is odd, the next term is 3 times the previous term plus 1

For example, starting from 12, we get the Collatz sequence: 12, 6, 3, 10, 5, 16, 8, 4, 2, 1

The Collatz conjecture states that all Collatz sequences will eventually reach 1. This has not been proven. This module allows you to test the conjecture by making your own Collatz sequences.

To create and plot a Collatz sequence, run a python file containing code like this:

from collatz import Collatz
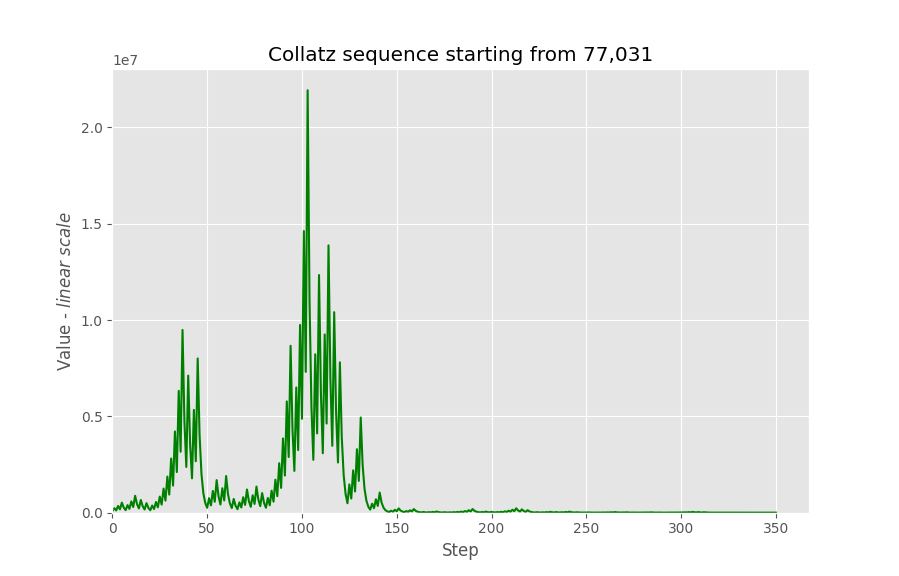
# Create a Collatz sequence starting from 77,031 (until it reaches 1)
sequence = Collatz(77031)
# Plot the sequence
sequence.plot()

You can change the scale of the y-axis:

# Plot the sequence with log y-axis scale
sequence.plot(scale='log')

To compare multiple Collatz sequences on a single plot:

from collatz import Collatz, plot_comparison
sequences = [Collatz(1017), Collatz(1016), Collatz(1015)]
plot_comparison(sequences)

As above, but using log scale:

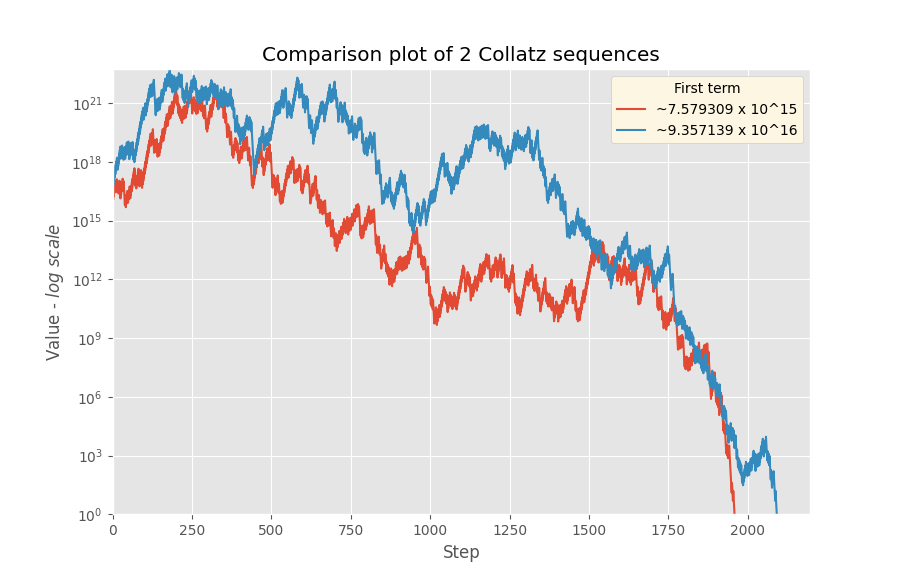
from collatz import Collatz, plot_comparison
sequence_1 = Collatz(7579309213675935)
sequence_2 = Collatz(93571393692802302)
plot_comparison([sequence_1, sequence_2], scale='log')

1. Ensure you have Python >= 3.6 installed

2. Download and unzip this repository

3. In the terminal, cd into the collatz/collatz/ folder

4. Run the following command:

   pip install .