Official implementation of several experiments in the paper "**Π-nets: Deep Polynomial Neural Networks**" (CVPR'20) and its extension (T-PAMI'21; also available here ).
Each folder contains a different experiment. Please follow the instructions in the respective folder on how to run the experiments and reproduce the results. This repository contains implementations in MXNet, PyTorch and Chainer.
The folder structure is the following:
face_recognition: The folder contains the code for the face verification and identification experiments.image_generation_chainer: The folder contains the image generation experiment on Chainer; specifically the experiment without activation functions between the layers.image_generation_pytorch: The folder contains the image generation experiment on PyTorch; specifically the conversion of a DCGAN-like generator into a polynomial generator.mesh_pi_nets: The folder contains the code for mesh representation learning with polynomial networks.classification-NO-activation-function: The folder contains the code for Π-nets without activation functions on classification (e.g. ImageNet).
A one-minute pitch of the paper is uploaded here. We describe there what generation results can be obtained even without activation functions between the layers of the generator.
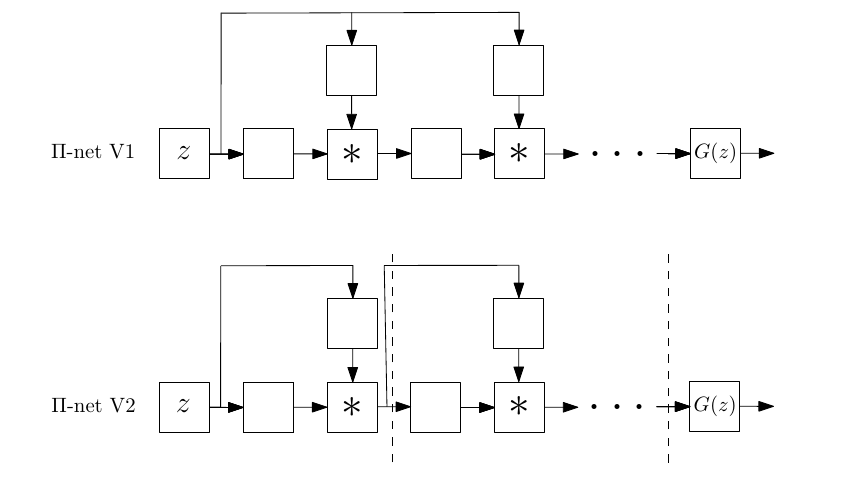
Π-nets do not rely on a single architecture, but enable diverse architectures to be built; the architecture is defined by the form of the resursive formula that constructs it. For instance, we visualize below two different Π-net architectures.
The evaluation in the paper [1] suggests that Π-nets can improve state-of-the-art methods. Below, we visualize results in image generation and errors in mesh representation learning.
The image above shows synthesizes faces. The generator is a Π-net, and more specifically a product of polynomials.
Color coded results of the per vertex reconstruction error on an exemplary human body mesh. From left to right: ground truth mesh, first order SpiralGNN, second, third and fourth order base polynomial in Π-nets. Dark colors depict a larger error; notice that the (upper and lower) limbs have larger error with first order SpiralGNN.
If you use this code, please cite [1] or (and) [2]:
BibTeX:
@inproceedings{
poly2020,
title={$\Pi-$nets: Deep Polynomial Neural Networks},
author={Chrysos, Grigorios and Moschoglou, Stylianos and Bouritsas, Giorgos and Panagakis, Yannis and Deng, Jiankang and Zafeiriou, Stefanos},
booktitle={Conference on Computer Vision and Pattern Recognition (CVPR)},
pages={7325--7335},
year={2020}
}
BibTeX:
@article{poly2021,
author={Chrysos, Grigorios and Moschoglou, Stylianos and Bouritsas, Giorgos and Deng, Jiankang and Panagakis, Yannis and Zafeiriou, Stefanos},
journal={IEEE Transactions on Pattern Analysis and Machine Intelligence},
title={Deep Polynomial Neural Networks},
volume={44},
number={8},
pages={4021--4034},
year={2021},
doi={10.1109/TPAMI.2021.3058891}}
| [1] | (1, 2) Grigorios G. Chrysos, Stylianos Moschoglou, Giorgos Bouritsas, Yannis Panagakis, Jiankang Deng and Stefanos Zafeiriou, Π-nets: Deep Polynomial Neural Networks, Conference on Computer Vision and Pattern Recognition (CVPR), 2020. |
| [2] | Grigorios G. Chrysos, Stylianos Moschoglou, Giorgos Bouritsas, Jiankang Deng, Yannis Panagakis and Stefanos Zafeiriou, Deep Polynomial Neural Networks, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021. |