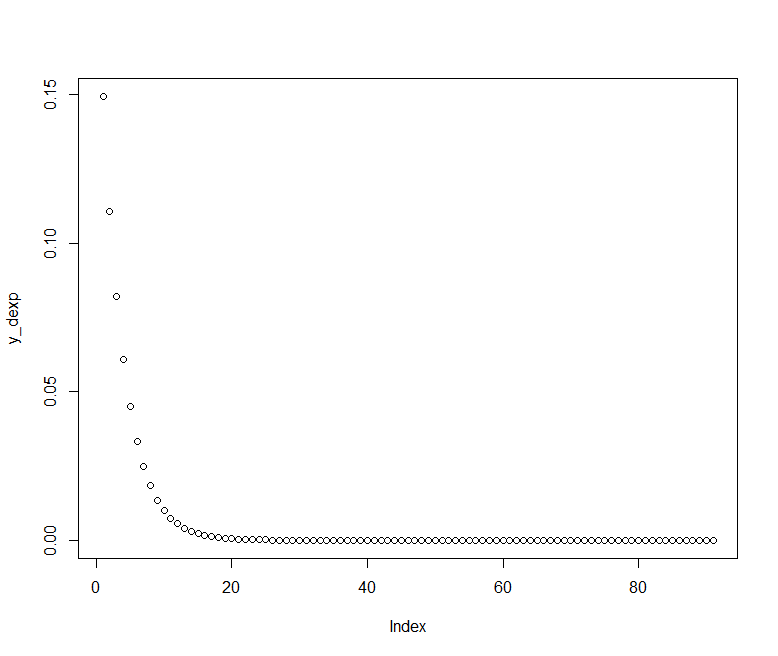Dimas Fadilah Akbar_5025211010
Kelas Probstat A

• R for windows
• RStudio

• library Rlab
• library dplyr
• library ggplot

pada praktikum ini akan menggunakan fungsi-fungsi yang tersedia pada library Rlab, dplyr, dan ggplot. Untuk itu perlu melakukan instalasi dengan mengetikkan code berikut pada console di RStudio

install.packages("Rlab")
install.packages("dplyr")
install.packages("ggplot2")

dalam menyelesaikan soal tersebut dapat menggunakan fungsi dgeom khusus untuk distribusi geometrik

n = 3
p = 0.20
output = dgeom(x = n, prob = p)
print(output)

output:

0.1024

• dalam menentukan distribusi geometriknya dapat menggunakan fungsi rgeom
• dalam menentukan mean dari distribusi geometrik dapat menggunakan fungsi mean

code :

rand <- 10000
p <- 0.20
m = mean(rgeom(n = rand, prob = p) == 3)
print(m)

output pada percobaan pertama:

0.0997

output pada percobaan kedua:

0.1036

pada subsoal a didapatkan nilai yang konstan dan tidak berubah sedangkan pada subsoal b didapatkan nilai yang berubah-ubah. Hal tersebut menunjukkan bahwa distribusi geometrik pada a sama dan distribusi geometrik pada b acak

code: Berikut merupakan generate berdasarkan peluangnya dengan menggunakan fungsi dgeom

library(ggplot2)
library(dplyr)

data.frame(x = 0:5, prob = dgeom(x = 0:5, prob = p)) %>%
  mutate(Failures = ifelse(x == n, n, "other")) %>%
  ggplot(aes(x = factor(x), y = prob, fill = Failures)) +
  geom_col() +
  geom_text(
    aes(label = round(prob,2), y = prob + 0.01),
    position = position_dodge(0.9),
    size = 3,
    vjust = 0
  ) +
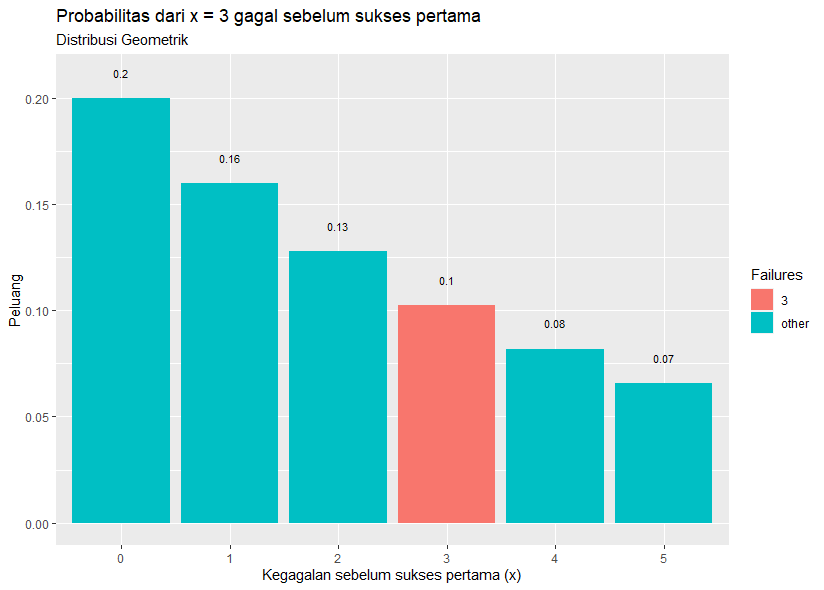
  labs(title = "Probabilitas dari x = 3 gagal sebelum sukses pertama",
       subtitle = "Distribusi Geometrik",
       x = "Kegagalan sebelum sukses pertama (x)",
       y = "Peluang") 

output:

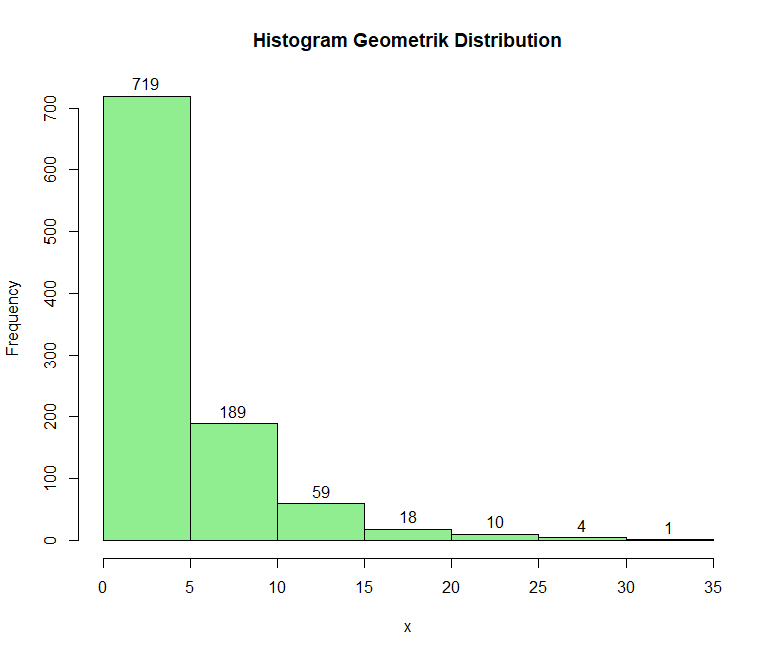
code : Berikut merupakan generate dengan distribusi acak menggunakan fungsi rgeom

x <- rgeom(1000, 0.20)
hist(x, main = "Histogram Geometrik Distribution", labels = T, col = "lightgreen")

output:

• formula dalam menentukan rataan di distribusi geometrik adalah (1/p).
• formula dalam menentuka varian di distribusi geomtrik adalah (1-p)/p^2

code:

p <- 0.20
rataan = (1/p)
varian = ((1-p)/p^2)
print(paste("rataan: ", as.character(rataan)))
print(paste("varian: ", as.character(varian)))

output:

"rataan: 5"
"varian: 20"

Dalam menentukan peluang pada distribusi binomial dapat menggunakan fungsi dbinom dengan 3 parameter yaitu:

• x menyatakan sukses
• p sebagai peluang sukses
• n sebagai total partisipan.

code:

n = 20
p = 0.2
x = 4
print(paste("Peluang 4 pasien sembuh: ", as.character(dbinom(x, n, p))))

output:

"Peluang 4 pasien sembuh:  0.218199401946101"

menentukan distribusi binomial dalam bentuk grafik histogram

code : menentukan peluangnya dan visualisasi dengan plot untuk x dari 0 hingga 20

n <- 20
p <- 0.2
x <- array(0:20)
plot(x, dbinom(x, n, p),
     type="h",
     main="Distribusi Binomial",
     ylab = "Probabilitas"
     )

output:

code : histogram dengan random nilai 20 dan peluang 0.20

n <- 20
size <- 20
p <- 0.20
x <- rbinom(n, size, p)
hist(x, main = "Histogram Binomial Distribution", labels = T, col = "lightgreen")

output:

• rataan (μ) pada distribusi binomial dapat dicari dengan rumus n*p
• varian (σ²) pada distribusi binomial dapat dicari dengan rumus np(1-p)

code :

n <- 20
p <- 0.2
rataan = n*p
varian = n*p*(1-p)
print(paste("rataan distribusi binomial(µ): ", rataan))
print(paste("varian distribusi binomial(s²): ", varian))

output:

"rataan distribusi binomial(µ):  4"
"varian distribusi binomial(s²):  3.2"

Dalam menentukan peluang pada distribusi poisson dapat menggunakan fungsi dpois dengan dua parameter yaitu:

• x => menyatakan banyaknya sukses yang terjadi
• lambda => menyatakan rata-rata banyaknya sukses yang terjadi pada interval waktu atau daerah tertentu

code :

x <- 6
lambda <- 4.5
peluang = dpois(x, lambda)
print(paste("probabilitas distribusi poisson 6 bayi lahir: ", peluang))

output:

"probabilitas distribusi poisson 6 bayi lahir:  0.128120143864584"

dalam menentukan frekuensi banyaknya bayi yang lahir dalam jangka waktu 365 hari kita dapat menggunakan fungsi rpois dengan dua parameter:

• n => inverval waktu atau daerah
• lambda => rata-rata banyaknya sukses pada interval waktu atau daerah tertentu

code :

set.seed(2)
n <-365
lambda <- 4.5
x <- rpois(n, lambda)
hist(x,main="Histogram Poisson Distribution",labels=T, col = "orange")

output:

apabila peluang yang didapatkan pada point a dikalikan dengan interval waktunya yaitu 365 maka akan didapatkan hasil yang hampir sama. Yang artinya peluang lahirnya bayi pada interval waktu 365 hari tidak jauh dari peluang distribusi poissonnya dalam pada interval satu hari.

• rataan (μ) pada distribusi poisson merupakan lambda
• varian (σ²) pada distribusi poisson juga merupakan lambda

code :

lambda <- 4.5
rataan = lambda
varian = lambda
print(paste("rataan distribusi poisson: ", rataan))
print(paste("varian distribusi poisson: ", varian))

output:

"rataan distribusi poisson:  4.5"
"varian distribusi poisson:  4.5"

Dalam menentukan probabilitas dari distribusi chi-square kita dapat menggunakan fungsi dchisq dengan dua parameter yaitu:

• x => variable peubah acak kontinu
• v => derajat bebas

code :

x <- 2
v <- 10
print(paste("probabilitas distribusi chi-square: ", dchisq(x, v)))

output :

"probabilitas distribusi chi-square:  0.00766415502440505"

code :

set.seed(2)
n <- 100
v <- 10
x <- rchisq(n, v)
hist(x, main="Histogram Chi-Square Distribution", labels = T, col = "orange")

output :

• rataan (μ) pada distribusi chi-square dapat dicari dengan nilai v
• varian (σ²) pada distribusi chi-square dapat dicari dengan rumus 2v

code :

rataan = v
varian = 2*v
print(paste("rataan distribusi chi-squre: ", rataan))
print(paste("varian distribusi chi-square: ", varian))

output :

"rataan distribusi chi-squre:  10"
"varian distribusi chi-square:  20"

Dalam menentukan probabilitas dari distribusi eksponensial kita dapat menggunakan fungsi dexp dengan 2 parameter:

• x => menyatakan x-values untuk exp function
• rate => represents the shapex.

code : Pada soal hanya diketahui rate nya saja yaitu 3 sehingga kita perlu membuat vector dari x nya yaitu dari 1 hingga 10 dengan kenaikan nilai sebanyak 0.1

rate <- 3
x_dexp = seq(1, 10, by = 0.1)
y_dexp = dexp(x_dexp, rate)
plot(y_dexp)

output :

Dalam membuat distribusi eksponensial untuk bilangan jumlah bil random yang telah ditentukan kita dapat menggunakan fungsi rexp dengan dua parameter:

• n => banyak bilangan random
• rate => represents the shapex

code :

rate <- 3
n1 <- 10
n2 <- 100
n3 <- 1000
n4 <- 10000
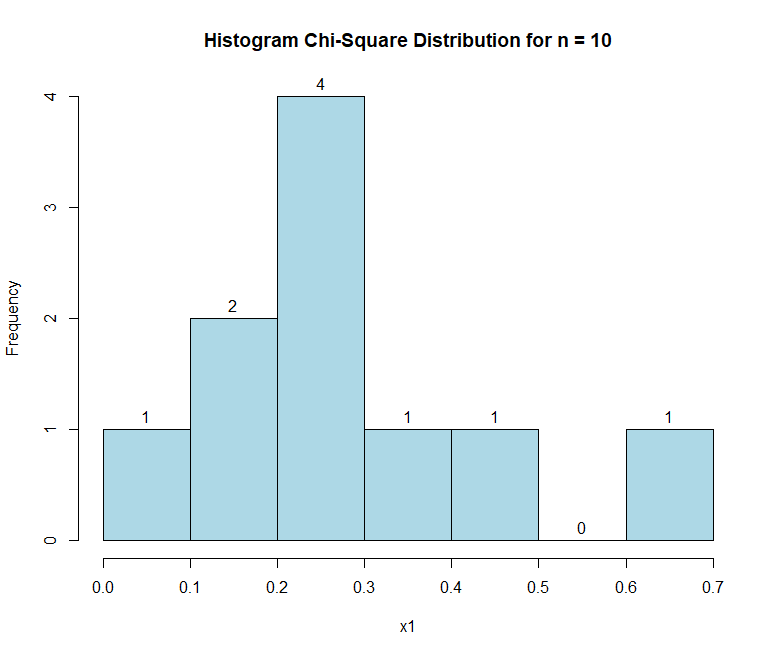
x1 = rexp(n1, rate)
x2 = rexp(n2, rate)
x3 = rexp(n3, rate)
x4 = rexp(n4, rate)
hist(x1, main = "Histogram Chi-Square Distribution for n = 10", labels = T, col = "lightblue")
hist(x2, main = "Histogram Chi-Square Distribution for n = 100", labels = T, col = "lightblue")
hist(x3, main = "Histogram Chi-Square Distribution for n = 1000", labels = T, col = "lightblue")
hist(x4, main = "Histogram Chi-Square Distribution for n = 10000", labels = T, col = "lightblue")

output:

Petunjuk:

• Gunakan set.seed(1)
• Gunakan fungsi bawaan R

code :

n <- 100
rate <- 3
set.seed(1)
rataan = mean(rexp(n, rate))
varian = sd(rexp(n, rate)) ^ 2
print(paste("Rataan distribusi eksponensial: ", rataan))
print(paste("Varian distribusi eksponensial: ", varian))

output:

"Rataan distribusi eksponensial:  0.343558812019206"
"Varian distribusi eksponensial:  0.0656076521452312"

Keterangan :

• X1 = Dibawah rata-rata
• X2 = Diatas rata-rata Contoh data :
• 1,2,4,2,6,3,10,11,5,3,6,8
• rata-rata = 5.083333
• X1 = 5
• X2 = 6

code :

n <- 100
rataan <- 50
sd <- 8
data_mean = mean(rnorm(n, rataan, sd))
data = rnorm(n, rataan, sd)
x1 = floor(data_mean)
x2 = ceiling(data_mean)

z_scores = (data - data_mean) / sd(data)

plot(z_scores, type = 'o', col = "darkmagenta")

output :

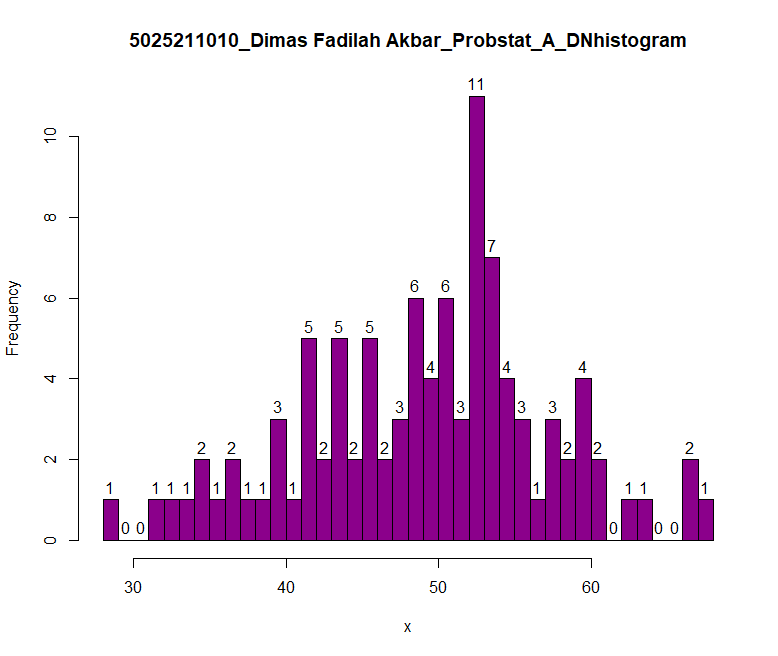
• NRP_Nama_Probstat_{Nama Kelas}_DNhistogram Contoh :
• 312312312_Rola_Probstat_A_DNhistogram

code :

n <- 100
rataan <- 50
sd <- 8
x <- rnorm(n,rataan,sd)
hist(x,
     breaks = 50,
     main = "5025211010_Dimas Fadilah Akbar_Probstat_A_DNhistogram", col = "darkmagenta", labels = T)

output:

code :

n <- 100
rataan <- 50
sd <- 8
varian = var(rnorm(n, rataan, sd))

print(varian)

output: percobaan pertama

62.93885

percobaan kedua

68.46113