Deepwave provides wave propagation modules for PyTorch, for applications such as seismic imaging/inversion. You can use it to perform forward modelling and backpropagation, so it can simulate wave propagation to generate synthetic data, invert for the scattering potential (RTM/LSRTM), other model parameters (FWI), initial wavefields, or source wavelets. You can use it to integrate wave propagation into a larger chain of operations with end-to-end forward and backpropagation. Deepwave enables you to easily experiment with your own objective functions or functions that generate the inputs to the propagator, letting PyTorch's automatic differentiation do the hard work of calculating how to backpropagate through them.

To install it, I recommend first installing PyTorch using the instructions on the PyTorch website. Deepwave can then be installed using

    pip install deepwave

The documentation contains examples and instructions on how to install and use Deepwave. You might also like to watch a video summary of Deepwave.

• Supports the 2D constant density acoustic / scalar wave equation (regular and Born modelling) and 2D elastic wave equation (P-SV)
• Runs on CPUs and appropriate GPUs
• The gradient of all outputs (final wavefields and receiver data) can be calculated with respect to the model parameters (wavespeed, scattering potential, etc.), initial wavefields, and source amplitudes
• Uses the Pasalic and McGarry PML for accurate absorbing boundaries in the scalar wave propagator
• Uses C-PML with the W-AFDA free-surface method for the elastic wave propagator
• The PML width for each edge can be set independently, allowing a free surface (no PML) on any side
• Finite difference accuracy can be set by the user
• A region of the model around the sources and receivers currently being propagated can be automatically extracted to avoid the unnecessary computation of propagation in distant parts of the model
• Double backpropagation through the regular scalar propagator, including calculating the Hessian

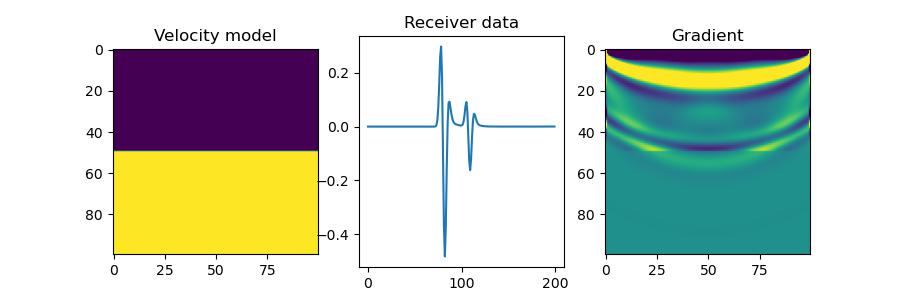
In a few lines you can make a velocity model, propagate a wave from a source in the top left corner to a receiver in the top right, calculate an objective function, and backpropagate to obtain its gradient with respect to the velocity.

import torch
import deepwave
import matplotlib.pyplot as plt

v = 1500 * torch.ones(100, 100)
v[50:] = 2000
v.requires_grad_()

out = deepwave.scalar(
    v, grid_spacing=4, dt=0.004,
    source_amplitudes=deepwave.wavelets.ricker(25, 200, 0.004, 0.06).reshape(1, 1, -1),
    source_locations=torch.tensor([[[0, 0]]]),
    receiver_locations=torch.tensor([[[0, 99]]])
)

(out[-1]**2).sum().backward()

_, ax = plt.subplots(1, 3, figsize=(9, 3))
ax[0].imshow(v.detach())
ax[0].set_title("Velocity model")
ax[1].plot(out[-1].detach().flatten())
ax[1].set_title("Receiver data")
ax[2].imshow(v.grad.detach(), vmin=-1e-5, vmax=1e-5)
ax[2].set_title("Gradient")

There are more examples in the documentation.

If you would like to cite Deepwave, I suggest:

@software{richardson_alan_2023,
  author       = {Richardson, Alan},
  title        = {Deepwave},
  month        = sep,
  year         = 2023,
  publisher    = {Zenodo},
  version      = {v0.0.20},
  doi          = {10.5281/zenodo.8381177},
  url          = {https://doi.org/10.5281/zenodo.8381177}
}