A classic implementation of the famous 2D Ising Model, written in C++. This was done as a project for Cooperative and Critical Phenomena, a subject for the Master in Physics of Complex Systems offered by the Institute of Cross-Disciplinary Physics and Complex Systems. The code is mostly based in the implementation by Raul Toral in his book Stochastic Numerical Methods: an Introduction for Students and Scientists.

The Ising Model is a model for a ferromagnetic - paramagnetic transition in magnetic materials, which has been studied as a reference model for phase transitions. It is formed by spins up or down, which can interact. Spins tend to align, but temperature makes them flip. However, in the stationary distribution the statistical properties of the ensable are fixed. For example, this is how the material looks at the critical point in a space of size 512x512:

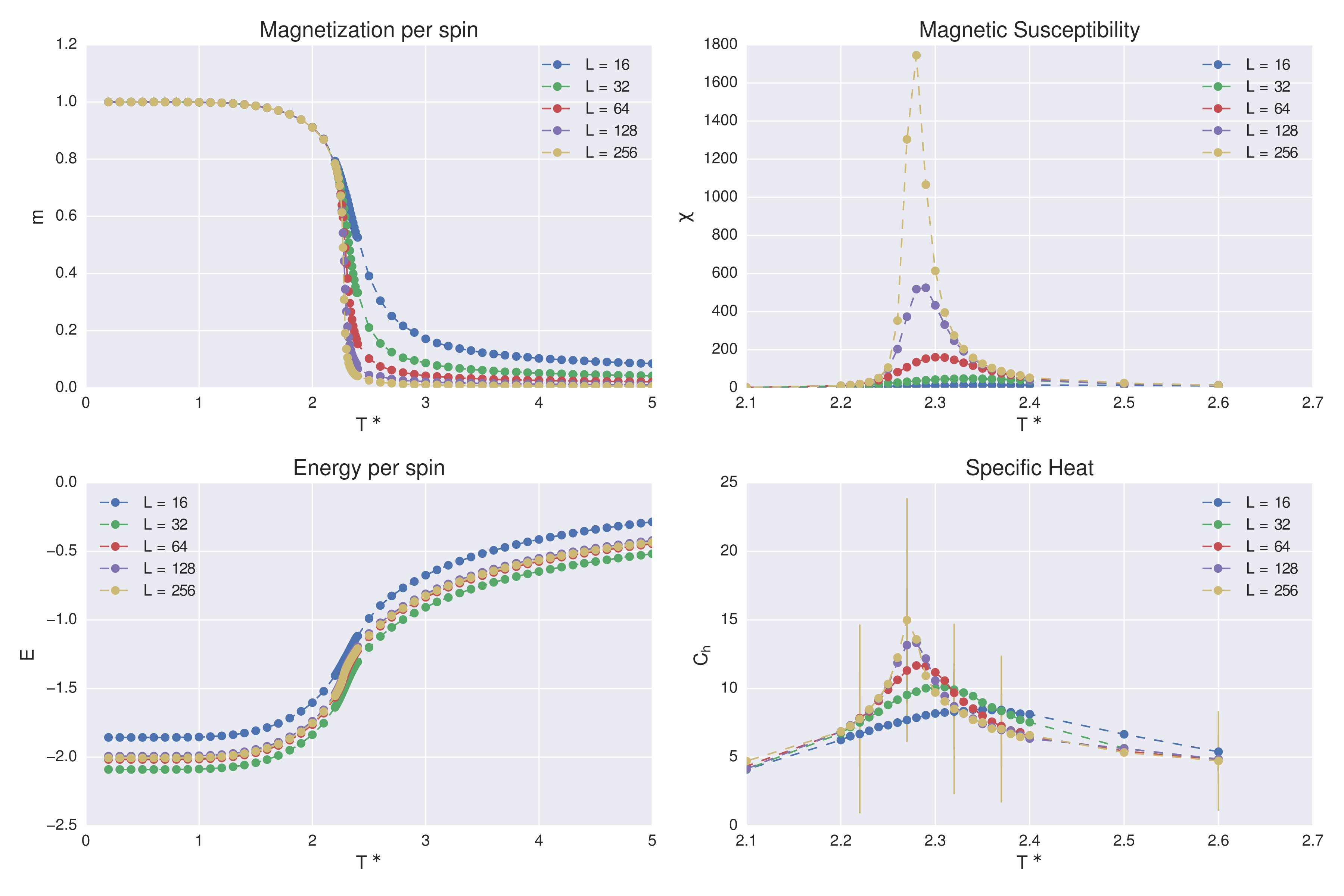
The program computes the magnetization, susceptibility, energy and specific heat in the stationary state. Far away the critical point, the Metropolis algorithm was used to reach this state. Near the critical temperature, we change to Wolff collective to do it in a fast way. Once we are in the stationary state, we take several measures, updating enough steps between measurements in order to avoid statistical correlations. In the next graph you can see the observables, for several system sizes:

The next step is to compute critical temperature, as well as critical exponents. For the critical temperature, Binder cumulant is used. This quantity is constant exactly at the critical point, so we try to compute where all the graphs, for different sizes, converge. In practice, we take pairs and make an average:

Finally, once all the temperature and the critical exponents have been computed, we can check the scaling function. The result is pretty beautiful, and it possible to see the collapse of all the sizes near the critical points:

The C++ code may be not very readable, and the program takes time to do all the measurements. However, I hope you find it a useful reference: it is pretty well optimized, and all the errors are carefully computed.