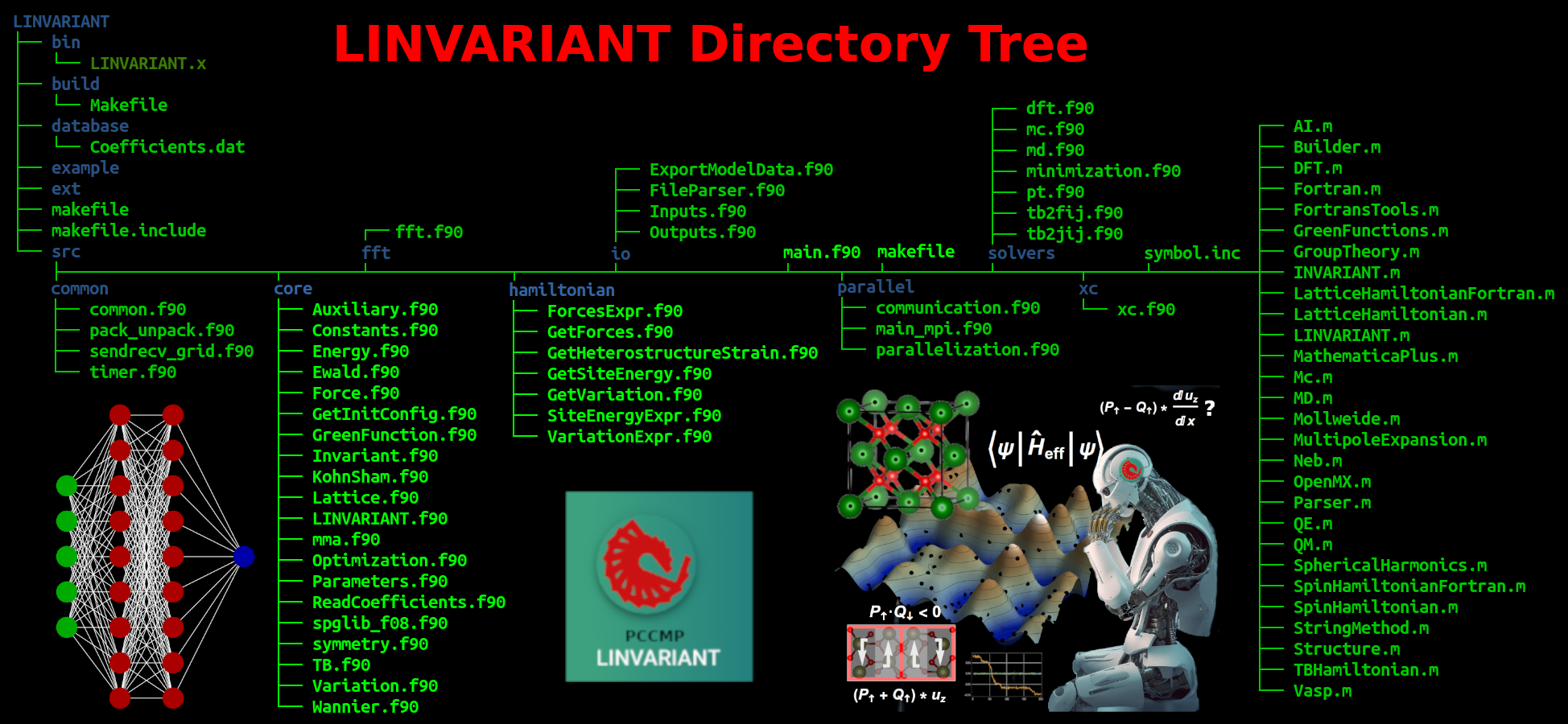
LINVARIANT is a first-principles-based model effective Hamiltonian software package for the atomistic simulations of realistic materials. The goals are to reach large scales and keep being predictive.
INVARIANT is a property of a mathematical object (or a class of mathematical objects) that remains unchanged after operations or transformations of a certain type are applied to the objects.
L is to memorize famous physicist Lev Davidovich Landau (22 January 1908 – 1 April 1968).

• LINVARIANT takes care of multi-physics systems such as lattice, electron, spin, and their interactions.
• LINVARIANT is capable of generating both microscopic and phenomenological models.
• LINVARIANT learns/analysis the symmetry of the interaction forms and generates their DFT training accordingly.
• LINVARIANT solves the models with many numerical solvers, such as MC, MD, Exact diagonalization, Minimization, etc.
• For large-scale calculations, LINVARIANT exports FORTRAN code from symbolic models.

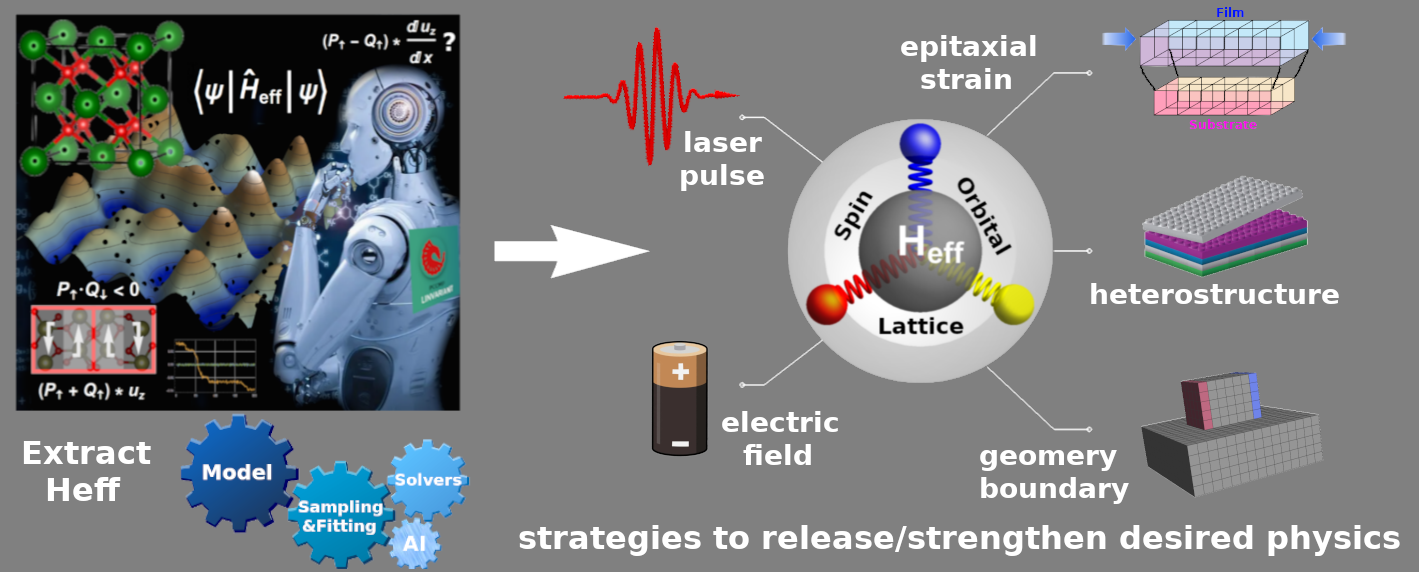
• Lattice models for structural phase transitions, such as Landau-Ginzburg-Devonshire models.
• Magnetic models for (non-)collinear spins, such as the extended Heisenberg model.
• Electronic models, such as the Tight-Binding model written in Wannier orbitals.
• Full models with couplings among lattice, orbitals, and spins.
• Models in zero-, one-, two, and three-dimension.
• Neural Network Potential (NNP)

• (1) Finite Element Method (FEM), (2) Minimization, (3) molecular dynamics (MD), (4) Monte Carlo (MC), and (5) Finite Differences nonlinear solver on the large-scale continuous model
• Parallel tempering algorithm is available with both MC and MD

• Basis (ionic): phonon/irreducible representation/atomistic basis
• Basis (electronic): pseudo-atomic/Wannier basis
• searching crystal structures by machine learning of the energy invariants
• walking around (sampling) the potential energy surface by machine learning the symmetry of the energetic coupling terms.

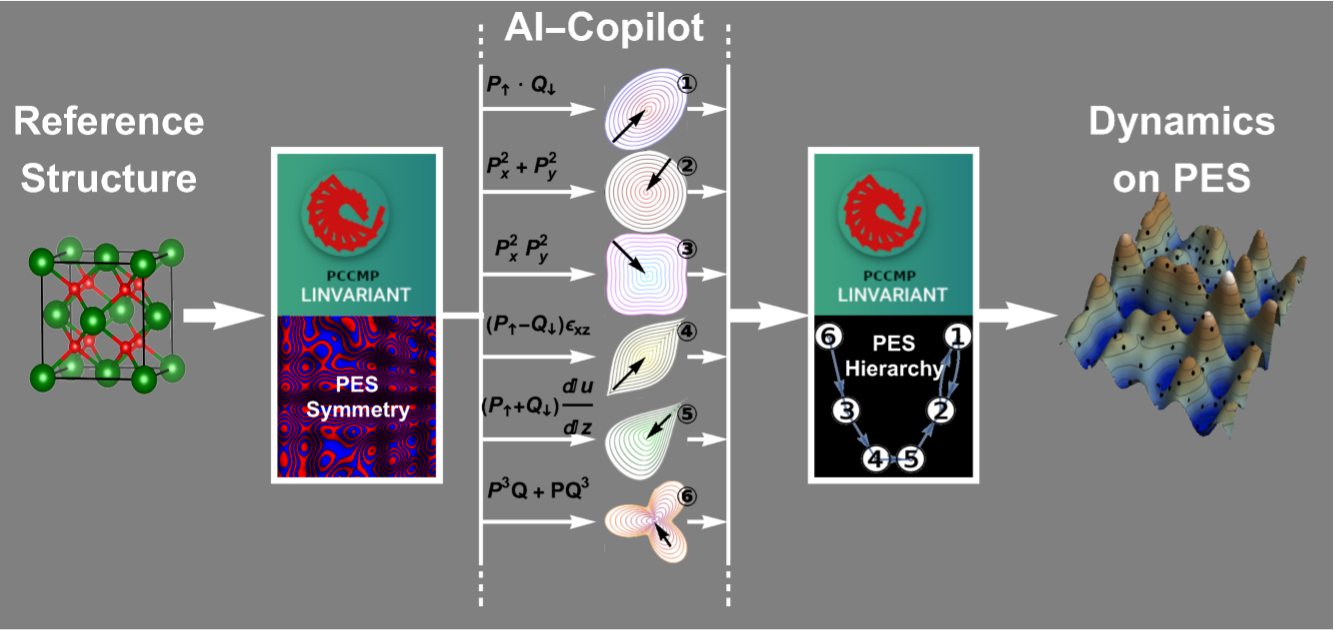
• Write Fortran (numerical) using mathematica (symbolic)
• interface to VASP, Quantum Espresso, and OpenMX
• interface to WANNIER90
• mpi and openmp parallelization
• dynamics under external electric field
• Jij of Heisenberg model from DFT by Liechtenstein formalism
• Fij (force constants) from tight-binding models (atomistic Green's function method)
• Electron/phonon bands unfolding
• phonon/magnon calculations from DFT input
• X ray diffraction simulation
• Nudged Elastic Bands (NEB) and Growing String Method (GSM) to explore the phase transition, dynamics, and domain wall structures
• Mollwide projection

• Boracite, Perovskite (To be added: Spinel, Rutile, Pyrochlore)

• implement the k dot p model builder
• adding transport property calculations
• including electron-phonon coupling (EPC) beyond first-order w.r.t. phonons.

• Microscopic origin of the electric Dzyaloshinskii-Moriya interaction, Phys. Rev. B 106, 224101 (2022).
• Deterministic control of ferroelectric polarization by ultrafast laser pulses, Nat. Commun. 13, 2566 (2022)
• Dzyaloshinskii-Moriya-like interaction in ferroelectrics and anti-ferroelectrics, Nat. Mater. 20, 341 (2021)
• Domain wall-localized excitations from GHz to THz, npj Comput. Mater. 6, 48 (2020)
• Improper ferroelectricities in 134-type AA’3B4O12 perovskites, Phys. Rev. B 101, 214441 (2020).

• Peng Chen - [email protected]
• Hongjian Zhao - [email protected]
• Sergey Artyukhin - [email protected]
• Laurent Bellaiche - [email protected]
  See also the list of contributors who participated in this project.