A Python made program for solving the statement of Topic 17.
Python 3.4 and above (tested on Python 3.6.8). It can be downloaded here.
It can be downloaded right here (choose between ZIP or TAR.GZ as you prefer).
Extract it and open a terminal window on the directory where it was extracted.
Execute main.py in terminal and follow the instructions to add and convert automata.
python main.py
Execute demo.py in terminal to convert the automata example.
python demo.py
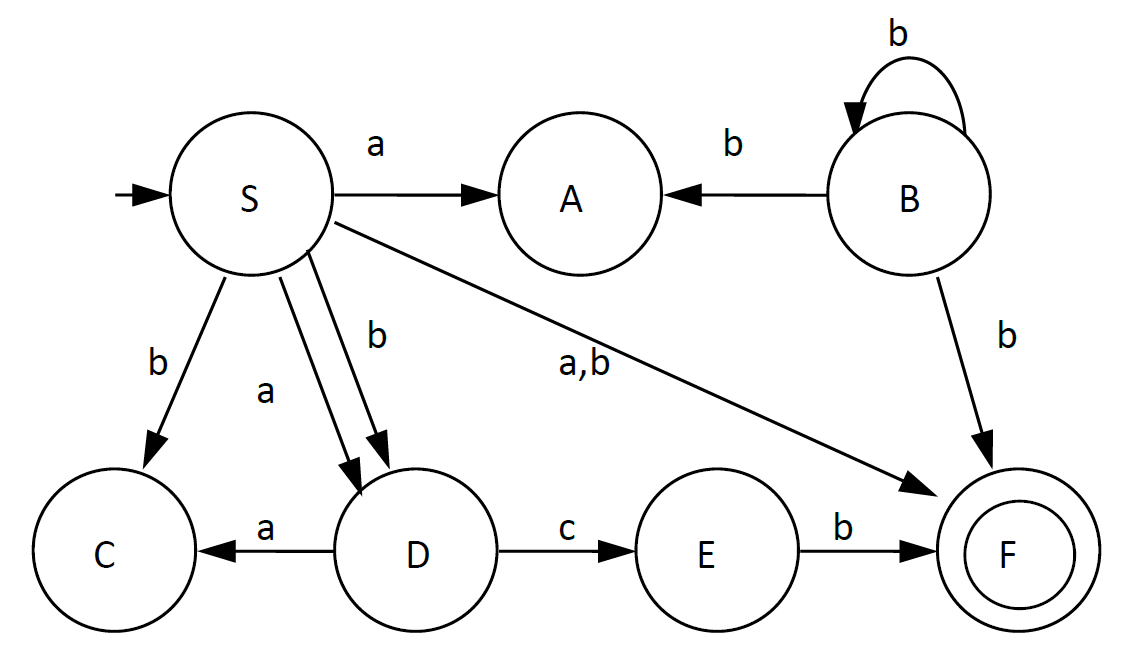
Given a finite automaton (A), it is asked to write a finite automaton (A’) that fulfills the following condition:
- L(A’)={xy, x ∈ L(A), y ∉ L(A)}
- Convert the finite automaton to a complete deterministic one.
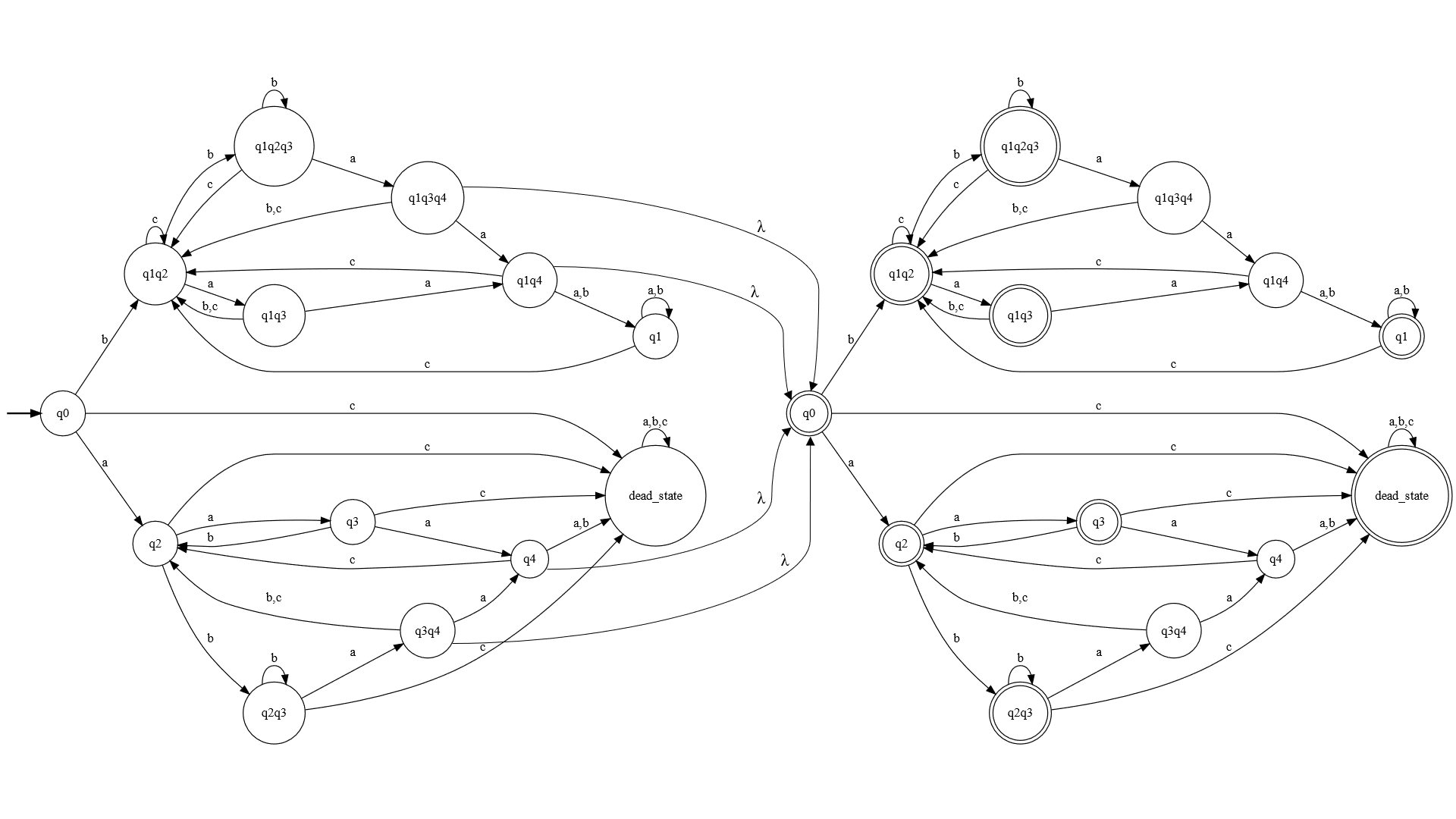
- Algorithm to eliminate empty transitions (lambda).
- Algorithm for converting a NFA to a DFA.
- Reduce DFA: no useless states (not accessible and not co-accessible).
- Complete DFA: for each pair (state, letter) there is transition -> "dead state".
- Calculate complement of the complete DFA from the previous step.
- As the DFA is complete, it will be enough to indicate that the final states are not and vice versa.
- Concatenate the DFA calculated in the first step with its complement calculated in the second step.
- It will be enough to create empty transitions (lambda) between the set of final states of the first automaton and the initial state of the second automaton, being the new set of final states those of the second automaton.
- OPTIONAL: eliminate the empty transitions (lambda) of the previous step.
- This step is performed by the program; however, in the example below it has not been performed to facilitate the understanding of the algorithm.
ER1:
a(a(b+ac))(aa+bb(a((c+b+ac)(a(b+ac))bba)(a+(c+b+ac)(a(b+ac))(a+bb)a+$)+a))+bc((a+(b+a((c+b)ca)((c+b)cb+a((c+(b+a)(a+b)c)ca((c+b)ca)a)(c+(b+a)(a+b)c)c(b+a((c+b)ca)(c+b)cb)))(b+cc(b+a((c+b)ca)((c+b)cb+a((c+(b+a)(a+b)c)ca((c+b)ca)a)(c+(b+a)(a+b)c)c(b+a((c+b)ca)(c+b)cb))))cca)((c+b)ca)(a+a((c+(b+a)(a+b)c)ca((c+b)ca)a)(
NOTE: the automata presented in this README have lambda transitions to make them easier to understand. This program returns automata without lambda transitions.