ECG

2024-02-16
2024-06-11

ECG Data Processing

Introduction

Here we apply a methodological approach used in processing ECG data, as detailed in ./ecg_process/ecg_process.R. Our process emphasizes the integrity of data handling, leveraging automated methods to ensure reproducibility and objectivity, particularly suitable for preparing data for subsequent statistical analysis.

Process Overview

1. Initial Data Visualization

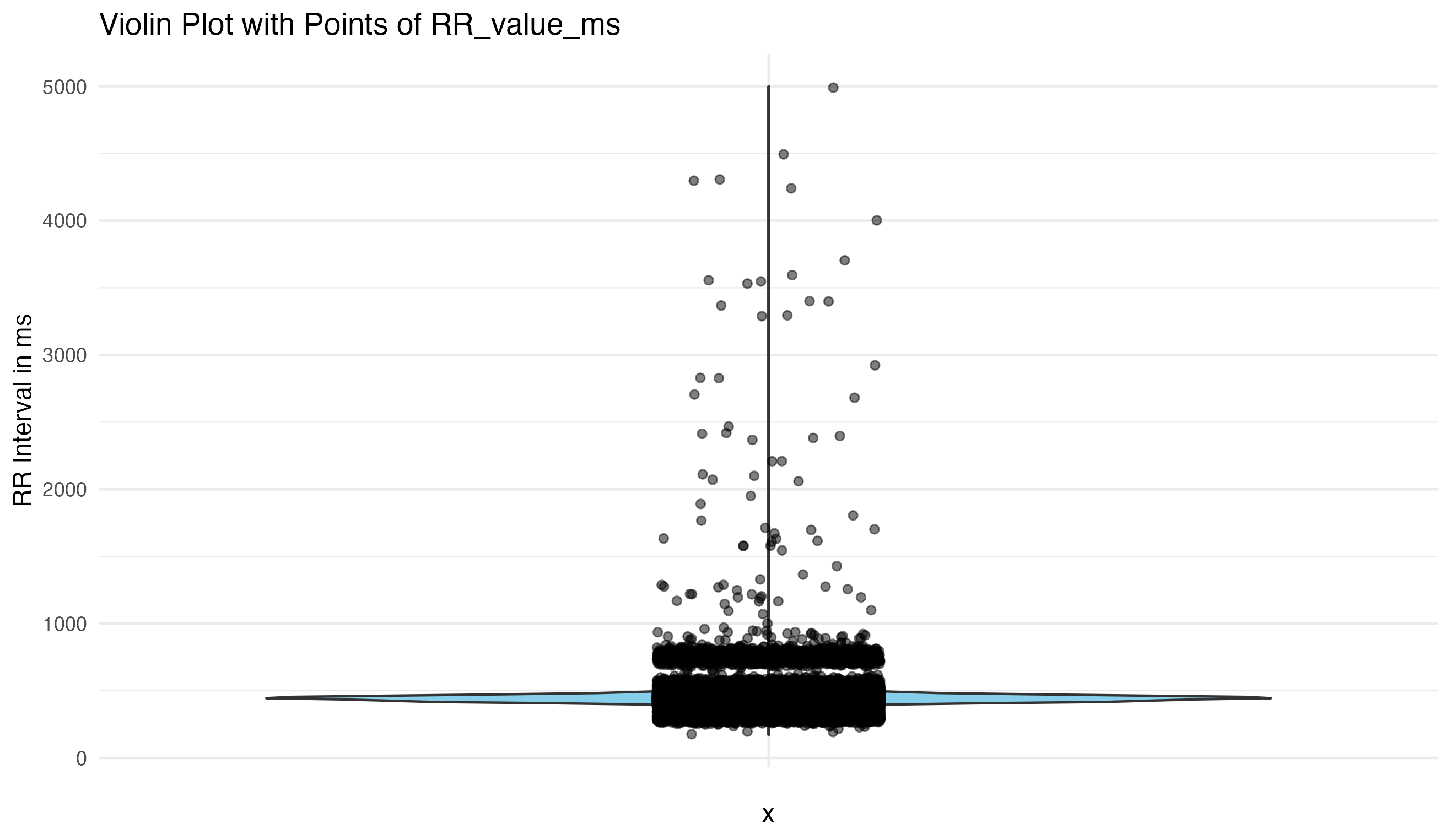
Visualizing the data is the first critical step, allowing us to understand the inherent characteristics and identify obvious anomalies or noise. This approach guides our subsequent data cleaning efforts, ensuring we base our decisions on empirical evidence rather than assumptions.

Initial Visual Assessment:

2. Automated Data Cleaning and Clustering

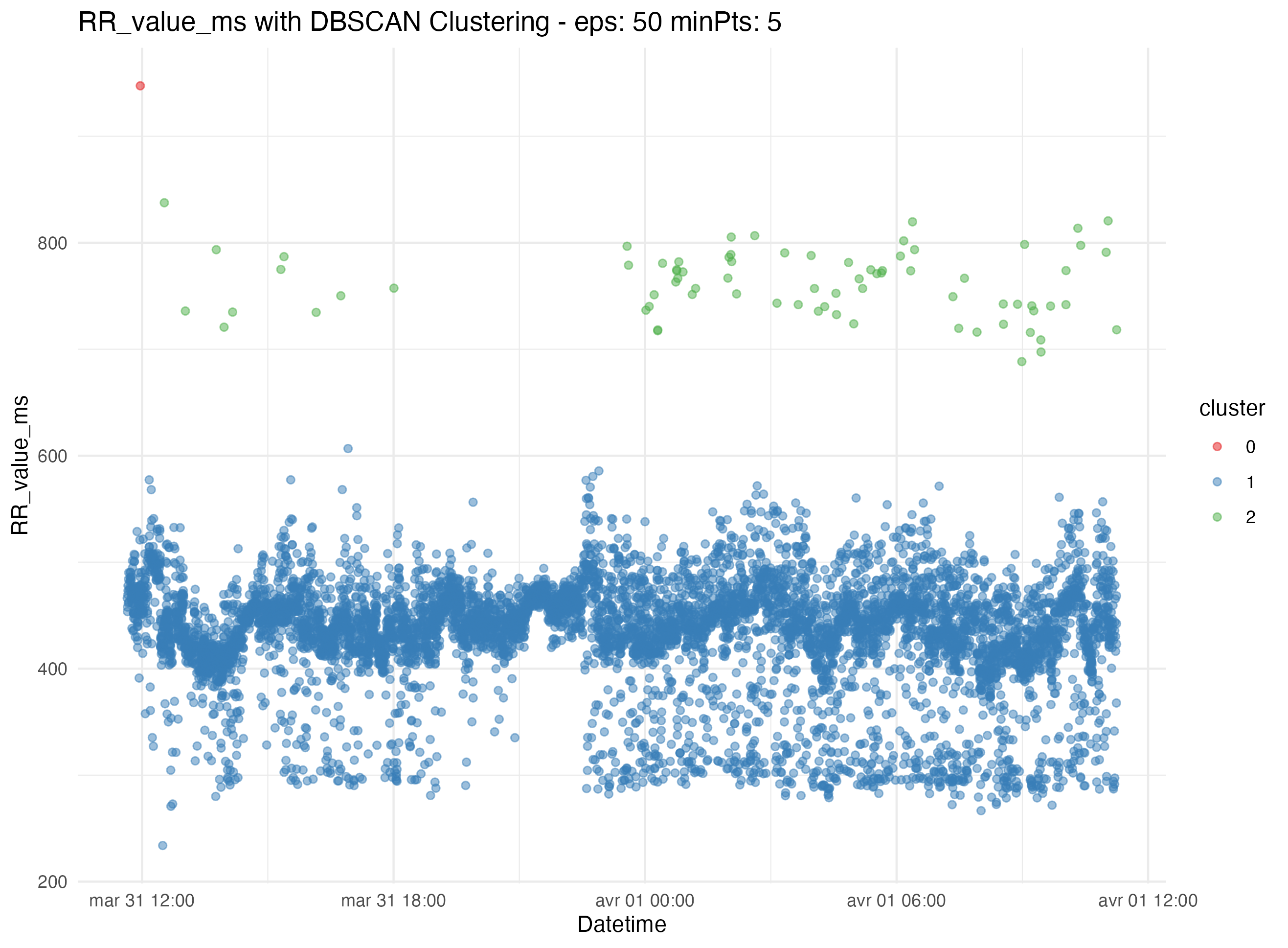
First we try to find the outlier thresholds using simple methods like interquartile range (IQR). This does not work for us, so we move to more advanced clustering algorithms like K-means, Z-score, DBSCAN. In our dataset DBSCAN works best, so we automatically segregate data into clusters to further identify and eliminate outliers and artifacts. This method enhances the reliability of the dataset by minimizing manual intervention and potential bias.

Clustering and Outlier Detection:

3. Data Integrity and Filtering

By applying statistical thresholds derived from the data distribution itself, we automate the filtering of noise and outliers. This step is crucial for maintaining data integrity, allowing the visualization to guide our interpretation and adjust our methods accordingly.

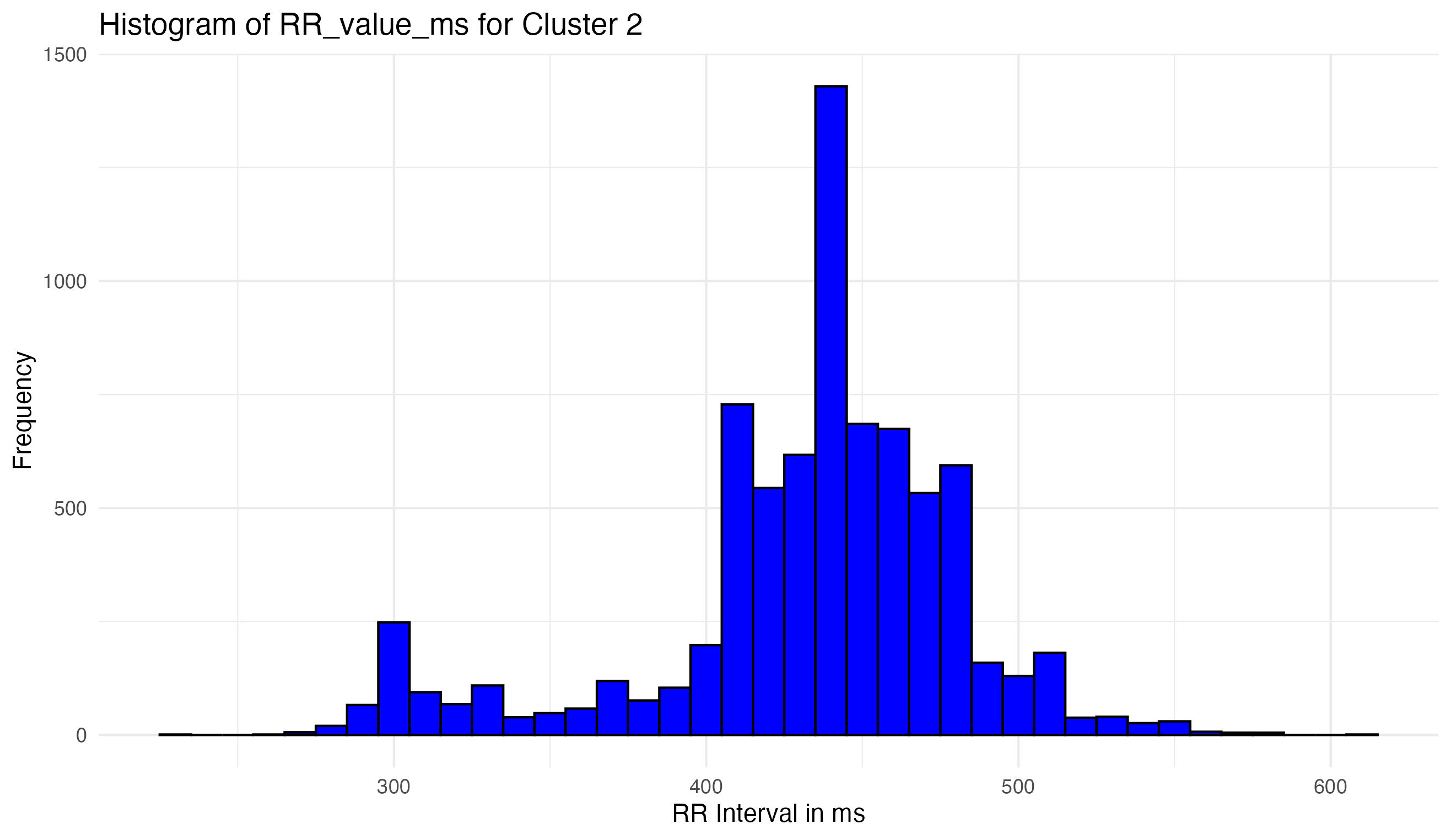
Refinement and Validation:

Visualization of the cleaned data ensures the removal of artifacts while preserving true signals.
Continuous validation against the original data characteristics confirms that the cleaning process enhances data quality without distorting fundamental features.

4. Preparation for Statistical Analysis

The cleaned and validated dataset is now primed for robust statistical analysis, ensuring that any findings or conclusions drawn are based on high-quality data.

Conclusion

The steps outlined here demonstrate our commitment to rigorous data processing, leveraging visualization not just for initial assessment but as an integral part of continuous validation throughout the cleaning process. For further details on the commands and specific methods used, please refer to the R script located at ./ecg_process/ecg_process.R.

ECG Data Simulation

ECG waveform simulation and analysis

This set of examples focuses on the simulation and analysis of Electrocardiogram (ECG) waveforms to study Heart Rate Variability (HRV) in a controlled, simulated environment. Using custom R functions for ECG waveform generation, we explore the effects of different conditions (control vs. case groups) on HRV, incorporating covariates such as age, sex, and treatment types in our analysis. The goal is to illustrate the application of statistical or machine learning methods, including Generalized Linear Models (GLM), to understand the potential influences on heart rate signals.

Features

ECG Simulation: Utilizing logistic map-based simulations to generate synthetic ECG waveforms, mimicking real heart rate variability patterns.
Peak Detection: Implementing basic algorithms to identify R peaks within the ECG waveforms, a critical step for HRV analysis.
Covariate Integration: Including simulated demographic and treatment data to examine the broader impacts on HRV.
Statistical Analysis: Applying t-tests for initial comparisons and GLMs to account for multiple covariates, aiming to uncover any significant differences in HRV between groups.
Visualization: ggplot2 for visualization of ECG data, analysis results, and the effects of covariates.

Load custom ECG simulation functions

source("./ecg_functions.R")
library(ggplot2)
library(dplyr)

Illustration of ECG wave

Prepare dataset

Initial setup for ECG waveform simulation.
Define the total number of heartbeats and other parameters for ECG simulation.

T <- 3  # Total heart beats
P1 <- 0.5  # Starting value for the logistic map
r <- 3.0  # Logistic map parameter
cons <- 0.0  # Constant added to logistic map output
SAMPLING_RATE <- 125  # Sampling rate for the ECG in Hz

Simulate ECG data
Generate P vector using logistic map

P <- numeric(T)
P[1] <- P1
for (i in 2:T) {
  P[i] <- r * P[i - 1] * (1 - P[i - 1])
}
P <- P + cons

Convert P vector to Q vector and simulate ECG waveform

Q <- cumsum(P)
ecg <- fit_ecg_waves_to_beats(Q, sampling_rate=SAMPLING_RATE)
t <- seq_along(ecg) / SAMPLING_RATE

Plot simulated ECG waveform

ecg_data <- data.frame(Time = t, ECG = ecg)
head(ecg_data)

##    Time         ECG
## 1 0.008  0.81412525
## 2 0.016  0.66425004
## 3 0.024  0.50441533
## 4 0.032  0.34482331
## 5 0.040  0.08031695
## 6 0.048 -0.20324786

Peak detection

Step 1: Detect peaks - Find local maxima
A simple approach to find local maxima (peaks)

find_peaks <- function(ecg_data) {
  peaks <- which(diff(sign(diff(ecg_data$ECG))) == -2) + 1
  peak_data <- ecg_data[peaks, ]
  return(peak_data)
}

peak_data <- find_peaks(ecg_data)

Step 2: Filter peaks by separation - ensure they are at least 0.4s apart (assumption)
Sort peaks by amplitude to get the highest peaks first

sorted_peaks <- peak_data[order(-peak_data$ECG), ]
filtered_peaks <- sorted_peaks[1, ]  # Initialize with the highest peak

for (i in 2:nrow(sorted_peaks)) {
  if (all(abs(filtered_peaks$Time - sorted_peaks$Time[i]) >= 0.4)) {
    filtered_peaks <- rbind(filtered_peaks, sorted_peaks[i, ])
    if (nrow(filtered_peaks) == 2) break  # Stop after finding the second peak
  }
}

Step 3: Plot and annotate the ECG waveform with R peaks

p <- ggplot(ecg_data, aes(x = Time, y = ECG)) +
  geom_line() +
  geom_point(data = filtered_peaks, aes(x = Time, y = ECG), color = "red", size = 3) +
  geom_text(data = filtered_peaks, aes(x = Time, y = ECG, label = "R"), vjust = -2, color = "red") +
  labs(title = "Simulated ECG Waveform with R Peak detection", x = "Time (s)", y = "Amplitude (mV)") +
  theme_minimal()

# print(p)

# Calculate the time difference between the two peaks
if (nrow(filtered_peaks) >= 2) {
  time_diff <- diff(filtered_peaks$Time)
  time_diff_label <- paste(round(time_diff, 2), "s")

  # Coordinates for annotation placement
  x_midpoint <- sum(filtered_peaks$Time) / 2
  y_max <- max(ecg_data$ECG) * 1.1

  # Add a line connecting the two peaks and annotate it with the time difference
  p <- p + geom_segment(aes(x = filtered_peaks$Time[1], y = max(ECG),
                            xend = filtered_peaks$Time[2], yend = max(ECG)),
                        linetype = "dashed", color = "blue") +
    annotate("text", x = x_midpoint, y = y_max, label = time_diff_label, color = "blue")
}

print(p)

Example of full dataset

Initial setup for ECG waveform simulation

# Define the total number of heartbeats and other parameters for ECG simulation

T <- 20  # Total heart beats
P1 <- 0.5  # Starting value for the logistic map
r <- 3.0  # Logistic map parameter
cons <- 0.0  # Constant added to logistic map output
SAMPLING_RATE <- 125  # Sampling rate for the ECG in Hz

Simulate ECG data.
Generate P vector using logistic map.

P <- numeric(T)
P[1] <- P1
for (i in 2:T) {
  P[i] <- r * P[i - 1] * (1 - P[i - 1])
}
P <- P + cons

Convert P vector to Q vector and simulate ECG waveform

Q <- cumsum(P)
ecg <- fit_ecg_waves_to_beats(Q, sampling_rate=SAMPLING_RATE)
t <- seq_along(ecg) / SAMPLING_RATE

Plot simulated ECG waveform

ecg_data <- data.frame(Time = t, ECG = ecg)

ggplot(ecg_data, aes(x = Time, y = ECG)) +
  geom_line() +
  labs(title = "Simulated ECG Waveform", x = "Time (s)", y = "Amplitude (mV)") +
  theme_minimal()

Simulate HRV data for case/control study

Simulate RR intervals with variability for two groups: control and case

N <- 100  # Number of RR intervals per group
control_rr <- simulate_rr_intervals_group(N, 0.8, 0.05, "Control")
case_rr <- simulate_rr_intervals_group(N, 0.8, 0.15, "Case")
hrv_data <- rbind(control_rr, case_rr)

Summarize HRV metrics for each group

hrv_summary <- hrv_data |>
  group_by(Group) |>
  summarise(Mean_RR = mean(RR_Interval),
            SDNN = sd(RR_Interval),
            RMSSD = sqrt(mean(diff(RR_Interval)^2)))

head(hrv_summary)

## # A tibble: 2 × 4
##   Group   Mean_RR   SDNN  RMSSD
##   <chr>     <dbl>  <dbl>  <dbl>
## 1 Case      0.808 0.0901 0.135 
## 2 Control   0.800 0.0306 0.0423

Plot HRV data showing RR interval variability between groups

ggplot(hrv_data, aes(x = Group, y = RR_Interval)) +
  geom_boxplot() +
  geom_jitter(alpha = 0.5, width = 0.3, height = 0) +
  labs(title = "RR Interval Variability by Group", x = "Group", y = "RR Interval (s)") +
  theme_minimal()

Assess distribution of RR intervals for normality

# Plot histograms and Q-Q plots for visual inspection
ggplot(hrv_data, aes(x = RR_Interval, fill = Group)) +
  geom_histogram(bins = 30, alpha = 0.6) +
  facet_wrap(~Group) +
  labs(title = "Distribution of RR Intervals by Group", x = "RR Interval (s)", y = "Count") +
  theme_minimal()

# Q-Q plots for Control and Case groups using ggplot2
ggplot(hrv_data, aes(sample = RR_Interval)) +
  stat_qq() +
  stat_qq_line() +
  ggtitle("Q-Q Plot for Control Group") +
  theme_minimal() +
  facet_grid(.~Group, scales="free")

Perform Shapiro-Wilk test for normality

shapiro_test_control <- shapiro.test(hrv_data$RR_Interval[hrv_data$Group == "Control"])
shapiro_test_case <- shapiro.test(hrv_data$RR_Interval[hrv_data$Group == "Case"])
print(shapiro_test_control)

## 
##  Shapiro-Wilk normality test
## 
## data:  hrv_data$RR_Interval[hrv_data$Group == "Control"]
## W = 0.94082, p-value = 0.0002163

print(shapiro_test_case)

## 
##  Shapiro-Wilk normality test
## 
## data:  hrv_data$RR_Interval[hrv_data$Group == "Case"]
## W = 0.93559, p-value = 0.0001048

Decision on statistical test based on normality assessment
If normality is not rejected, use t-test; otherwise, consider Mann-Whitney U test.
Example of performing a t-test (replace with Mann-Whitney U test if necessary)

t_test_result <- t.test(RR_Interval ~ Group, data=hrv_data)
print(t_test_result)

## 
##  Welch Two Sample t-test
## 
## data:  RR_Interval by Group
## t = 0.8715, df = 121.53, p-value = 0.3852
## alternative hypothesis: true difference in means between group Case and group Control is not equal to 0
## 95 percent confidence interval:
##  -0.01055037  0.02714454
## sample estimates:
##    mean in group Case mean in group Control 
##             0.8084336             0.8001365

Generalised linear model (GLM)

In this section of our analysis, we employ a Generalized Linear Model (GLM) as a more sophisticated approach to analyzing our data, as opposed to relying solely on a t-test. The example of GLM framework is chosen for several reasons:

Incorporation of Multiple Covariates: Unlike the t-test, which is limited to comparing means between two groups, GLM allows us to account for the influence of multiple covariates simultaneously. This is crucial in our study, as we’re interested in understanding how factors such as age (Age_day), sex (Sex), and treatment type (Treatment) might impact Heart Rate Variability (HRV), alongside the primary variable of interest (Group).
Flexibility in Modeling Different Types of Data: GLM extends the general linear model to allow for response variables that have error distribution models other than a normal distribution. This makes it suitable for a wide range of data types and link functions, providing a more accurate analysis that aligns with the underlying data distribution.
Ability to Handle Non-linear Relationships: Through the use of link functions, GLMs can model relationships between the predictor and response variables that are not necessarily linear. This capability is particularly important in biomedical data, where many relationships are complex and non-linear.
Direct Estimation of Effect Size and Significance: GLMs provide direct estimates of the effect size for each covariate, including confidence intervals and p-values, making it easier to interpret the impact of each factor on the response variable. This comprehensive insight is invaluable in discerning not just if there is an effect, but how strong that effect is, and how confidently we can assert its presence.
Improved Precision and Power: By adjusting for additional covariates that might influence the response variable, GLMs can reduce unexplained variability in the data. This leads to more precise estimates of the effects of interest and potentially increases the statistical power of the analysis.

By leveraging a GLM, we’re not just comparing group means; we’re constructing a more nuanced understanding of how various factors contribute to differences in RR intervals, providing a deeper insight into the dynamics of heart rate variability. This approach allows us to make more informed conclusions about the data, supported by a robust statistical framework that accounts for the multifaceted nature of biological phenomena.

Covariate data

Simulating covariate data

set.seed(123)  # For reproducibility

covariate_data <- data.frame(
  Sample = 1:(2*N),  # Assuming N samples per group as before
  Age_day = sample(0:60, 2*N, replace = TRUE),
  Sex = sample(0:1, 2*N, replace = TRUE),
  Treatment = sample(c("a", "b", "c"), 2*N, replace = TRUE)
)

# Combine with HRV data
hrv_data <- cbind(hrv_data, covariate_data)
head(hrv_data)

##   RR_Interval   Group Sample Age_day Sex Treatment
## 1   0.7742978 Control      1      30   1         b
## 2   0.7938344 Control      2      14   1         a
## 3   0.8480075 Control      3      50   1         b
## 4   0.7611492 Control      4      13   0         b
## 5   0.7843837 Control      5       2   0         b
## 6   0.7632358 Control      6      41   1         a

# Convert necessary factors
hrv_data$Group <- as.factor(hrv_data$Group)
hrv_data$Sex <- as.factor(hrv_data$Sex)
hrv_data$Treatment <- as.factor(hrv_data$Treatment)

Fit GLM model

glm_model <- glm(RR_Interval ~ Group + Age_day + Sex + Treatment, data = hrv_data, family = gaussian())

# Summary of GLM results
summary(glm_model)

## 
## Call:
## glm(formula = RR_Interval ~ Group + Age_day + Sex + Treatment, 
##     family = gaussian(), data = hrv_data)
## 
## Deviance Residuals: 
##       Min         1Q     Median         3Q        Max  
## -0.156667  -0.035937   0.006798   0.039084   0.147207  
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.7999151  0.0142399  56.174   <2e-16 ***
## GroupControl -0.0086322  0.0096890  -0.891    0.374    
## Age_day       0.0004314  0.0002968   1.453    0.148    
## Sex1         -0.0077469  0.0097240  -0.797    0.427    
## Treatmentb    0.0047564  0.0121710   0.391    0.696    
## Treatmentc   -0.0065654  0.0122398  -0.536    0.592    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 0.004542105)
## 
##     Null deviance: 0.90077  on 199  degrees of freedom
## Residual deviance: 0.88117  on 194  degrees of freedom
## AIC: -503.39
## 
## Number of Fisher Scoring iterations: 2

Predicted vs. Actual RR Intervals Plot
This plot shows the relationship between the actual RR intervals and the predicted RR intervals from the GLM, providing insight into the model’s accuracy.

# Calculate predicted values
hrv_data$Predicted_RR <- predict(glm_model, type = "response")

# Plot of Actual vs. Predicted RR Intervals
ggplot(hrv_data, aes(x = Predicted_RR, y = RR_Interval)) +
  geom_point(aes(color = Group), alpha = 0.6) +
  geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "red") +
  labs(title = "Actual vs. Predicted RR Intervals", x = "Predicted RR Interval (s)", y = "Actual RR Interval (s)") +
  theme_minimal()

Residuals Plot
This plot examines the residuals (differences between actual and predicted values) to check for any systematic patterns that might suggest inadequacies in the model.

# Calculate residuals
hrv_data$Residuals <- residuals(glm_model)

# Residuals Plot
ggplot(hrv_data, aes(x = Predicted_RR, y = Residuals)) +
  geom_hline(yintercept = 0, linetype = "dashed", color = "red") +
  geom_point(aes(color = Group), alpha = 0.6) +
  labs(title = "Residuals vs. Predicted RR Intervals", x = "Predicted RR Interval (s)", y = "Residuals") +
  theme_minimal()

Effect Plot for a Single Covariate
To illustrate the effect of a single covariate while holding others constant, you can create a plot for one covariate at a time. Here’s an example for Age:

# Assuming 'Age' is a continuous variable in your model
ggplot(hrv_data, aes(x = Age_day, y = RR_Interval)) +
  geom_point(aes(color = Group), alpha = 0.6) +
  geom_smooth(method = "glm", method.args = list(family = "gaussian"), formula = y ~ x, aes(group = Group, color = Group)) +
  labs(title = "Effect of Age on RR Interval", x = "Age (days)", y = "RR Interval (s)") +
  theme_minimal()

Visualize effects of Group and Covariates on RR Interval

ggplot(hrv_data, aes(x = Group, y = RR_Interval, color = Group)) +
  geom_boxplot() +
  geom_point() +
  facet_wrap(~Sex + Treatment, scales = "free_x") +
  labs(title = "RR Interval Variability by Group with Covariates\n(sex 0/1, treatments a,b,c)", x = "Group", y = "RR Interval (s)") +
  theme_minimal()

Waveform notes

ECG simulation functions overview

The ecg_functions.R file includes custom functions designed for simulating Electrocardiogram (ECG) waveforms and analyzing Heart Rate Variability (HRV). These functions are used to generate synthetic ECG data, detect R peaks, simulate variability in RR intervals, and prepare data for case/control studies. The original inspiration for these functions came from the ecg_wave function from Tanzir Hasan’s ECG Simulation project.

Main Distribution Functions

The ECG waveform simulation leverages several key functions:

ecg_wave: Generates individual ECG wave components (P, Q, R, S, T waves) based on Fourier series expansions. Each wave represents different phases of the heart’s electrical activity.
fit_ecg_waves_to_beats: Combines the individual wave functions into a complete ECG waveform over a series of heartbeats, adjusted for heart rate variability.

Variability Functions

To analyze HRV, we introduce variability in the simulated RR intervals:

simulate_rr_intervals: Simulates RR intervals with specified baseline and variability, representing the time between successive R peaks.
rr_intervals_to_beats: Converts RR intervals into cumulative beats for further simulation, facilitating HRV analysis.

Simulating Groups

For our case/control study, we simulate groups with different HRV characteristics:

simulate_rr_intervals_group: Generates RR intervals for a specified group, incorporating baseline RR intervals and variability, useful for simulating control and case groups in our analysis.

README

Finally, automatically convert this document to the GitHub project level README.

file.copy("ecg_vcurrent.md", "README.md", overwrite = TRUE)

## [1] TRUE

Name		Name	Last commit message	Last commit date
Latest commit History 14 Commits
ecg_process		ecg_process
ecg_simulate		ecg_simulate
images		images
literature		literature
.DS_Store		.DS_Store
.gitignore		.gitignore
README.md		README.md

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

Repository files navigation

ECG

ECG Data Processing

Introduction

Process Overview

1. Initial Data Visualization

2. Automated Data Cleaning and Clustering

3. Data Integrity and Filtering

4. Preparation for Statistical Analysis

Conclusion

ECG Data Simulation

ECG waveform simulation and analysis

Features

Illustration of ECG wave

Prepare dataset

Peak detection

Example of full dataset

Simulate HRV data for case/control study

Generalised linear model (GLM)

Covariate data

Waveform notes

ECG simulation functions overview

Main Distribution Functions

Variability Functions

Simulating Groups

README

About

Releases

Packages

Languages

DylanLawless/ecg

Folders and files

Latest commit

History

Repository files navigation

ECG

ECG Data Processing

Introduction

Process Overview

1. Initial Data Visualization

2. Automated Data Cleaning and Clustering

3. Data Integrity and Filtering

4. Preparation for Statistical Analysis

Conclusion

ECG Data Simulation

ECG waveform simulation and analysis

Features

Illustration of ECG wave

Prepare dataset

Peak detection

Example of full dataset

Simulate HRV data for case/control study

Generalised linear model (GLM)

Covariate data

Waveform notes

ECG simulation functions overview

Main Distribution Functions

Variability Functions

Simulating Groups

README

About

Resources

Stars

Watchers

Forks

Releases

Packages 0

Languages

Packages