Convertisseur analogique-numérique

Symbole normé du convertisseur analogique-numérique.

Un convertisseur analogique-numérique (CAN, parfois convertisseur A/N, ou en anglais ADC pour Analog to Digital Converter ou plus simplement A/D) est un dispositif électronique dont la fonction est de traduire une grandeur analogique en une valeur numérique codée sur plusieurs bits. Le signal converti est généralement une tension électrique.

Le résultat de la conversion s'obtient par la formule : $N=2^{n}{V_{e} \over V_{\text{réf}}}$ où N est le résultat de conversion, V_e, la tension à convertir, n le nombre de bits du convertisseur et V_réf la tension de référence de la mesure.

Quantification

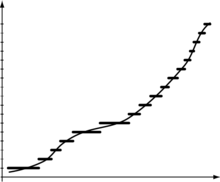
Le processus de conversion repose sur la quantification d'un signal c'est-à-dire par son appariement au niveau quantifié le plus proche (que l'on pourrait rapprocher du phénomène de l'arrondi pour les nombres à virgule).

La quantification d'un signal en dégrade sa richesse (il y a une perte d'information), c'est donc une transformation destructrice qui s’opère.

On appelle quantum, le pas minimum de conversion représenté par la variation du bit de poids faible, qui est aussi la valeur de l’imprécision de mesure. Plus le nombre n de bits du convertisseur sur lesquels s'effectuent la conversion est grand, plus la quantification a un effet réduit dans la dégradation du signal (sans jamais l'annuler).

Le quantum s'exprime comme la fraction élémentaire de la tension de référence (V_réf) divisée par la quantité de mesure possible ($2^{n}$, où n est le nombre de bits du convertisseur) : $q={V_{\text{réf}} \over 2^{n}}$ en volt (V).

Représentation de l'effet du nombre de bits du convertisseur sur la quantification d'un signal

Signal analogique en temps et amplitude continue.	Signal quantifié à basse résolution.	Signal quantifié à haute résolution.

Erreur de mesure

La mesure des convertisseurs repose sur la formule : $q=2^{n}{V_{e} \over V_{\text{réf}}}$.

Erreurs liées aux défauts de la référence

Il en ressort de cette formule qu'en dehors des défauts intrinsèques des convertisseurs, seule une variation intempestive de V_réf affecte la valeur de Q par la formule : ${\Delta q \over q}={{{2^{n}\cdot V_{e}} \over V_{\text{réf}}^{2}}\cdot \Delta V_{\text{réf}} \over {{2^{n}\cdot V_{e}} \over V_{\text{réf}}}}={\Delta V_{\text{réf}} \over V_{\text{réf}}}$.

Or cette variation de V_réf doit introduire une erreur de moins de ½ quantum à pleine échelle, ce qui se traduit par : ${\Delta V_{\text{réf}} \over V_{\text{réf}}}\leq {1 \over 2}{{V_{\text{réf}} \over 2^{n}} \over V_{\text{réf}}}\Leftrightarrow {\Delta V_{\text{réf}} \over V_{\text{réf}}}\leq {1 \over 2^{n+1}}$.

Cela signifie que la qualité des tensions de références (et au passage des tensions d'alimentation) des convertisseurs est un élément fondamental de leur mise en œuvre.

Tolérance relative des tensions de référence en fonction du nombre de bits

Nombre de bits	4 bits	8 bits	10 bits	12 bits	16 bits	20 bits	24 bits	32 bits
Tolérance	3,125 %	2 ‰	488 ppm	122 ppm	7,6 ppm	0,47 ppm	3 ppb	0,11 ppb

Erreurs liées au signal à convertir

L'autre source d'erreur est la variation de V_e dans le temps. La conversion n'étant pas instantanée, le signal doit rester stable pendant la mesure. Le signal V_e ne doit pas évoluer de plus d'un demi quantum pendant la phase de conversion, ce qui se traduit par une pente maximum pour le signal V_e :

${\frac {\Delta V_{e}}{\Delta t}}\leq {\frac {1}{2}}\cdot {\frac {V_{\text{réf}}}{2^{n}\cdot T_{e}}}$.

On applique donc impérativement un filtrage sur le signal V_e pour s'assurer qu'il n'est pas possible de se retrouver avec des pentes supérieures à celles qu'impose le convertisseur et qui sont en général plus restrictives que celles fixées par les règles de repliement de spectre, dont la fréquence de coupure est définie pour respecter le théorème de Shannon :

$F_{\text{max}}<{\frac {F_{e}}{2}}$.

L'utilisation de filtres induit des pertes supplémentaires d'information de signal puisque l'amplitude (A) de l'harmonique le plus proche du signal sinusoidal à la fréquence maximale (F_max) doit respecter la règle : $A\cdot 2\cdot \ \pi \cdot F_{\text{max}}\leq {\frac {1}{2}}\cdot {\frac {V_{\text{réf}}}{2^{n}\cdot T_{e}}}$.

Technologie des convertisseurs

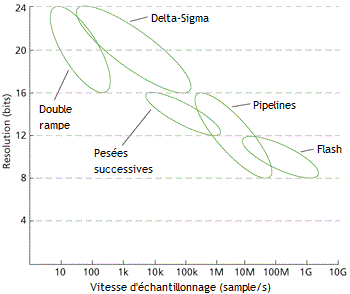
On dispose pour réaliser les conversions de plusieurs technologies de convertisseurs, chacune ayant des avantages et des inconvénients. Le choix de la technologie repose sur trois points :

• sa vitesse de conversion (la fréquence de son horloge ou sa fréquence d'échantillonnage) ;
• sa résolution (le nombre de bits) ;
• son coût.

Caractéristiques des familles technologiques des convertisseurs AN.

Convertisseur à simple rampe (objet fictif)

Schéma de principe d'un convertisseur analogique-numérique à simple rampe numérique.

Le convertisseur simple rampe est un objet fictif, ses performances sont trop mauvaises pour permettre son industrialisation. Il existe deux versions de ces convertisseurs, une analogique et une numérique, toutes deux non employées dans l'industrie.

La version analogique est relativement rapide mais très peu précise (en comparaison des autres convertisseurs utilisant des méthodes analogiques comme les convertisseurs à double rampe), là où la version numérique est précise mais lente (là encore en comparaison des autres convertisseurs utilisant des technologies numériques comme les convertisseurs à pesées successives).

Version analogique

On charge à courant constant, proportionnel à V_réf, une capacité C en comparant à l'aide d'un comparateur, la tension de la capacité V_cap à la tension à mesurer V_e. La charge de la capacité, depuis une tension nulle, jusqu'à V_réf, est réalisée en un temps T (période du convertisseur). Arrivé à la tension V_réf, la capacité est déchargée puis recommence un cycle de charge/décharge. La période d'échantillonnage est alors la durée d'un cycle de charge/décharge de la capacité.

On génère (à l'aide d'un comparateur) un signal à 1 pendant que V_cap < V_e et un signal à 0 pendant que V_cap ≥ V_e.

En mesurant la durée de l'impulsion (T_conv), on transforme un rapport de tension en un rapport de temps mesurable : ${T_{\text{conv}} \over T_{V_{\text{réf}}}}={V_{e} \over V_{\text{réf}}}$.

Ce type de convertisseur nécessite de fréquents recalibrages (en particulier sur la durée nécessaire à charger la capacité jusqu'à V_réf) pour pouvoir être fiable, un problème résolu sur les convertisseurs à double rampe.

Version numérique

Il est composé d'un compteur n bits, qui tant que l'entrée EN est à 1, compte au rythme de son horloge (H), dont la fréquence est $F_{\text{H}}=2^{n}\cdot F_{\text{e}}$ (avec F_e la fréquence d'échantillonnage).

La valeur numérique en sortie du compteur est convertie dans un convertisseur numérique-analogique ou CNA en une tension analogique V_a, qui est comparée à V_e.

Lorsque V_a devient plus grand que V_e, le comptage s'arrête et la valeur Q sur la sortie est le résultat de la conversion.

Ces convertisseurs ont les mêmes performances en termes de stabilité que les convertisseurs à approximations successives, tout en étant nettement plus lents que ces derniers avec des durées de comptage de $T_{\text{conversion}}=2^{n}\cdot T_{\text{horloge}}$, là où le convertisseur à pesées successives a un temps de conversion $T_{\text{conversion}}=(n+1)\cdot T_{\text{horloge}}$.

Convertisseur à double rampe

Fonctionnement d'un convertisseur à double rampe.

Le convertisseur à double rampe permet des conversions très précises en éliminant les effets de dérive des composants analogiques qu'il utilise, en particulier en annulant l'effet de dérive de la capacité. Son fonctionnement repose sur une comparaison entre une référence et le signal à convertir en mesurant les temps de charge et de décharge d'une capacité à l'aide d'un compteur sur n bits (n étant le nombre de bits du convertisseur).

La conversion se déroule en trois étapes :

• on charge une capacité avec un courant proportionnel au signal à convertir pendant un temps fixe (le temps du comptage complet du compteur) ;
• on décharge ensuite la capacité, avec un courant constant proportionnel à la tension de référence, jusqu'à annulation de la tension à ses bornes. Lorsque la tension devient nulle, la valeur du compteur est le résultat de la conversion ;
• on annule enfin la tension aux bornes de la capacité par une série convergente de charges et de décharges (l'objectif étant de décharger totalement la capacité pour ne pas fausser la mesure suivante). On parle en général de phase de relaxation.

Ces convertisseurs sont particulièrement lents (quelques dizaines de millisecondes par cycle, et parfois quelques centaines), et possèdent des résolutions souvent élevées (plus de 16 bits). Ils dérivent peu, dans le temps comme en température.

Technologiquement, les convertisseurs à double rampe ne sont sensibles qu'à la variation de la tension V_réf ou à une gigue de la fréquence de l'horloge, ce qui en fait l'un des convertisseurs les plus précis existant sur le marché.

Convertisseur Delta-Sigma

Schéma de principe d'un convertisseur Delta-Sigma.

Ce type de convertisseur est basé sur le principe du suréchantillonnage d'un signal d'entrée.

Le principe de fonctionnement d'un convertisseur Delta-Sigma repose sur l'utilisation d'un décimateur dans un système en contre-réaction.

Boucle de contre réaction

• On soustrait à la tension V_e, la tension V_c (issue du comparateur) pour produire la tension V_a (Delta).
• On intègre V_a pour produire la tension V_b (V_b = V_b + V_a) (Sigma).
• On compare V_b à 0 V pour produire une tension V_c qui vaut soit V_réf (1 logique) soit 0 V (0 logique).

Prenons l'exemple d'une conversion d'une tension de 3 V avec une tension de référence de 5 V.

On considère que l'intégrateur est à la base déchargé (V_b = 0 V). Or si V_b = 0 V alors V_c = 0 V.

• Début du premier cycle de mesure
  • V_a = V_e − V_c = 3 V − 0 V = 3 V
  • V_b = V_b + V_a = 0 + 3 V = 3 V
  • Si V_b = 3 V, V_c = V_réf = 5 V ⇒ Entrée d'un 1 logique dans le décimateur.
• Début du second cycle de mesure
  • V_a = V_e − V_c = 3 V − 5 V = −2 V
  • V_b = V_b + V_a = 3 V − 2 V = 1 V
  • Si V_b = 1 V, V_c = V_réf = 5 V ⇒ Entrée d'un 1 logique dans le décimateur.
• Début du troisième cycle de mesure
  • V_a = V_e − V_c = 3 V − 5 V = −2 V
  • V_b = V_b + V_a = 1 V − 2 V = −1 V
  • Si V_b = −1 V, V_c = 0 V ⇒ Entrée d'un 0 logique dans le décimateur.
• Début du quatrième cycle de mesure
  • V_a = V_e − V_c = 3 V − 0 V = 3 V
  • V_b = V_b + V_a = −1 V + 3 V = 2 V
  • Si V_b = 2 V, V_c = V_réf = 5 V ⇒ Entrée d'un 1 logique dans le décimateur.
• Début du cinquième cycle de mesure
  • V_a = V_e − V_c = 3 V − 5 V = −2 V
  • V_b = V_b + V_a = −2 V + 2 V = 0 V
  • Si V_b = 0 V, V_c = 0 V ⇒ Entrée d'un 0 logique dans le décimateur.
• Fin du cinquième cycle, on reboucle au premier cycle puisque V_b a la même valeur qu'au début du premier cycle.

Décimateur

Première mesure

Si on regarde les valeurs entrées dans le décimateur, on trouve la série 11010110101101011010... à l'infini tant que la tension en entrée V_e ou que V_réf ne varient pas.

Pour un convertisseur n bits, on va additionner les valeurs binaires des $2^{n}$ premiers termes (par exemple pour un convertisseur 4 bits, on additionne les seize premiers chiffres), ce qui revient à compter le nombre de bits à 1 dans la série des seize premiers chiffres pour obtenir le résultat de la conversion.

En appliquant cette méthode à l'exemple, on trouve pour les seize premiers bits : 1101011010110101. Soit 1 + 1 + 0 + 1 + 0 + 1 + 1 + 0 + 1 + 0 + 1 + 1 + 0 + 1 + 0 + 1 = 10.

Le résultat de la conversion est donc 10 (A en hexadécimal ou 1010 en binaire).

Donc 10 bits à 1 pour 16 bits.

On peut vérifier la validité de ce résultat en procédant à l'inverse : $V_{\text{mesure}}=V_{\text{réf}}{10 \over 16}$ ou ${50\,{\text{V}} \over 16}$ = 3,125 V avec une imprécision de mesure de plus ou moins un demi quantum (${V_{\text{réf}} \over 16}$ = 0,312 5 V) soit une tension comprise dans l'intervalle : 2,968 75 V ≤ V_e ≤ 3,281 25 V.

Si on applique cette mesure pour un convertisseur 10 bits (donc utilisant une série de 2¹⁰ = 1 024 mesures), on trouve la valeur 615 (il y a 615 bits à 1 dans la série de 1 024 bits) d'où un résultat de mesure : $V_{\text{mesure}}=V_{\text{réf}}{615 \over {2^{10}}}=5\,{\text{V}}{615 \over 1\,024}$ = 3,002 929 V avec une imprécision de mesure de 0,004 883 V.

Pour la première mesure, il faut donc attendre 2ⁿ échantillons avant de pouvoir produire un résultat de conversion.

Mesures suivantes

V_e n'évolue pas

Désormais on peut produire un résultat de conversion à chaque période de l'horloge d'échantillonnage.

Pour cela on soustrait du décimateur le résultat de la comparaison (échantillon) le plus ancien et on lui ajoute le nouveau résultat de comparaison. A chaque période de l'horloge, le convertisseur est capable de fournir une valeur qui va osciller autour de la valeur réelle mesurée.

Si on reprend le convertisseur 4 bits, la première série de mesure était : 1101011010110101. En éliminant le premier échantillon (1) et en entrant le suivant (1), on trouve la série 1010110101101011, ce qui donne à nouveau la valeur 10 (A en hexadécimal et 1010 en binaire) comme résultat de conversion ($V_{\text{mesure}}={10\cdot V_{\text{réf}} \over 16}$). Les résultats suivants seront : 9 (0101101011010110), puis 10 (1011010110101101), 9 (0110101101011010), 10, etc.

On crée donc un système asservi (puisque la sortie du comparateur est soustraite à l'entrée) qui fait osciller la valeur de l'intégrale du signal à convertir autour de la valeur à mesurer.

V_e évolue

Une variation de V_e va entrainer une variation progressive du résultat de la conversion, car le décimateur ne peut pas évoluer de plus d'un quantum par période d'échantillonnage, ce qui impose au signal à mesurer (V_e) de ne pas avoir d'évolution de sa valeur (ΔV), supérieure à un quantum par échantillon (${\Delta V \over T_{\text{e}}}\leq Q$).

Par exemple, dans le convertisseur 4 bits, si V_e passe soudainement de sa valeur d'origine (3 V) à 0 V, l'évolution du résultat ne sera pas un brusque passage à 0, mais une décroissance en 2ⁿ périodes.

Si V_e = 0 V, on ne rentrera plus que des 0 dans le décimateur, donc le résultat de la conversion passera de 10 (1101011010110101) à 9 (1010110101101010), puis 8 (0101101011010100), puis 8 à nouveau (1011010110101000), 7, 7, 6, 5, 5, 4, 4, 3, 2, 2, 1, 1 et enfin 0.

On a donc un comportement du convertisseur qui n'est pas acceptable, mais qui repose uniquement sur un non-respect de la règle d'utilisation, qui interdit des variations de V_e au delà de la gamme autorisée : ${\Delta V \over T_{\text{e}}}\leq Q$.

En revanche pour des évolutions inférieures à un quantum par période d'échantillonnage, le convertisseur est capable de fournir en continu, à chaque période de l'horloge d'échantillonnage, une valeur de conversion.

En utilisant une fréquence d'échantillonnage élevée (T_e diminue), on augmente la capacité du décimateur à suivre des évolutions rapides de V_e. On retrouve ici le principe du suréchantillonnage.

Caractéristiques

Le temps de conversion initial est donc long puisqu'il faut $2^{n}$ périodes pour que le décimateur dispose d'assez d'échantillons pour fournir une somme significative permettant la mesure, mais une fois cette première conversion réalisée, on peut obtenir un résultat à chaque période de l'horloge du décimateur.

De plus si la tension en entrée évolue lentement (moins d'un quantum par période d'échantillonnage), le convertisseur est capable de suivre le rythme et de fournir à chaque période de l'horloge un résultat de conversion, sans avoir besoin de vider l'intégrateur, ce qui permet de rendre le système d'autant plus réactif que la fréquence d'échantillonnage est grande.

La limite d'évolution du signal V_e dépendant à la fois du nombre de bits (n) et de la tension de référence (V_réf) et de la fréquence d'échantillonnage (F_e) sous la forme de $\Delta V_{\text{e}}\leq {V_{\text{réf}}\cdot F_{\text{e}} \over 2^{n}}$. Par exemple pour un convertisseur delta-sigma avec un V_réf à 5 V, une conversion sur 10 bits et fonctionnant à 1 MHz : ΔV ≤ 4,88 mV/µs. Et 48,83 mV/µs pour un échantillonnage à 10 MHz.

L'intérêt de ce genre de convertisseur réside dans sa grande résolution de sortie possible (16, 24, 32 bits voire plus) pour des signaux d'entrée avec une bande passante modérée.

Ces convertisseurs sont adaptés à la conversion de signaux analogiques issus de capteurs dont la bande passante est souvent faible (par exemple les signaux audio). Les convertisseurs Sigma-Delta sont, par exemple, utilisés dans les lecteurs de CD dans le cas d'une conversion numérique-analogique.

Les technologies Sigma-Delta ont quasi totalement remplacé les technologies à simple ou double rampe.

Les principaux défauts technologiques des Delta-Sigma, en plus de leur grande sensibilité à la valeur de V_réf (qui est un problème commun à tous les convertisseurs, mais particulièrement sensible quand le nombre de bits augmente fortement), viennent des hystérésis du comparateur (différence de seuils de basculement entre le passage de 1 à 0 et de 0 à 1) et l'intégrateur (dérive de l'intégration pendant la mesure liées aux courants de fuite des AOP).

Convertisseur à approximations successives

Très proches en termes de composition des convertisseurs à simple rampe numériques, les convertisseurs à approximations successives (successive-approximation ADC ; aussi appelés « convertisseurs à pesées successives ») utilisent un processus de dichotomie pour traduire numériquement une tension analogique.

Un séquenceur (généralement nommé SAR pour successive approximation register), couplé à un CNA, produit une tension analogique, qui est comparée au signal à convertir. Le résultat de cette comparaison est alors réintroduit dans le SAR, qui va le prendre en compte, pour la suite du processus de dichotomie, jusqu'à complétion.

Reprenons l'exemple de la conversion avec un convertisseur analogique-numérique 4 bits à pesées successives, avec un V_réf de 5 V, d'une tension analogique de 3 V.

Avant d'aller plus loin dans l'exemple, il faut identifier le rôle du CNA, qui génère des tensions allant de 0 V pour le code 0000 (0 en base 10) à 4,687 5 V pour le code 1111 (15 en base 10), qui est la valeur maximale que peut prendre la sortie du CNA.

À cause du CNA, un convertisseur à pesées successives délivre toujours une valeur par défaut (arrondie à l'entier inférieur).

Analyse pas à pas

• Le SAR positionne son bit de poids fort à 1.
  • Le CNA reçoit alors le code binaire 1000 qui se traduit par une tension $V={8 \over 16}V_{\text{réf}}$ = 2,5 V. Le résultat est comparé à V_e.
  • V_e étant plus grand que V, la sortie du comparateur entre un niveau logique 1 dans le SAR.
  • Le bit de poids fort est fixé à 1.
• Le SAR positionne le second bit de poids fort à 1.
  • Le CNA reçoit alors le code binaire 1100 qui se traduit par une tension $V={12 \over 16}V_{\text{réf}}$ = 3,75 V. Le résultat est comparé à V_e.
  • V_e étant plus petit que V, la sortie du comparateur entre un niveau logique 0 dans le SAR.
  • Le bit à 0 remplace le 1 pour le deuxième bit de fort.
• Le SAR positionne le troisième bit de poids fort à 1.
  • Le CNA reçoit alors le code binaire 1010 qui se traduit par une tension $V={10 \over 16}V_{\text{réf}}$ = 3,125 V. Le résultat est comparé à V_e.
  • V_e étant plus petit que V, la sortie du comparateur entre un niveau logique 0 dans le SAR.
  • Le bit à 0 remplace le 1 pour le troisième bit de fort.
• Le SAR positionne le quatrième bit de poids fort à 1.
  • Le CNA reçoit alors le code binaire 1001 qui se traduit par une tension $V={9 \over 16}V_{\text{réf}}$ = 2,812 5 V. Le résultat est comparé à V_e.
  • V_e étant plus grand que V, la sortie du comparateur entre un niveau logique 1 dans le SAR.
  • Le quatrième bit de poids fort est fixé à 1.

Le résultat final est disponible : 1001 en binaire ou 9 (en base 10 ou 16) avec une imprécision de 0,312 5 V, donc compris entre 2,812 5 V et 3,125 V.

Évolution du SAR

1	0	0	0		2,5 V	1
1	1	0	0		3,75 V	0
1	0	1	0		3,125 V	0
1	0	0	1		2,812 5 V	1

Caractéristiques

Les convertisseurs à approximations successives ont des temps de conversion de l'ordre de la microseconde, pour des résolutions d'une douzaine de bits environ. Les convertisseurs à pesées successives sont les convertisseurs analogiques-numériques les plus répandus, on retrouve généralement un ou plusieurs convertisseurs de ce type dans chaque microcontrôleur.

Outre les effets liés à l'utilisation d'un CNA (et traités précédemment) et la sensibilité à la tension V_réf, le convertisseur à pesée successive ne souffre que des effets d'hystérésis du comparateur.

Convertisseur flash

Structure d'un convertisseur flash.

Les convertisseurs Flash utilisent un réseau de 2ⁿ résistances pour produire $2^{n}-1$ tensions dans un réseau de diviseurs de tension, qui seront comparées à l'aide d'un réseau de $2^{n}-1$ comparateurs, avec la tension à convertir, puis on traduit le code obtenu en une valeur sur n bits au moyen d'une mémoire ou d'un bloc de logique combinatoire.

Le réseau de résistance qui produit ces tensions est composé de 2ⁿ résistances identiques qui doivent être ajustées lors de la fabrication pour avoir la valeur R identique, avec une tolérance qui dépend du nombre de bits utilisés.

Cette technique de conversion est très rapide, mais coûteuse en composants et donc utilisée pour les applications critiques comme la vidéo.

Il est difficile d'assurer une bonne linéarité de la conversion, car cela nécessite que toutes les résistances soient égales avec une précision d'autant plus grande qu'il y a un grand nombre de résistances.

Les convertisseurs Flash ont des temps de conversion inférieurs à la microseconde mais une résolution assez faible (de l'ordre de 8 bits) et sont souvent très chers.

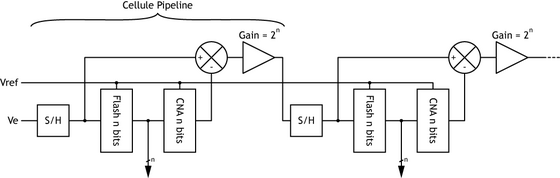
Convertisseurs semi-flash pipeline

Schéma de principe d'un convertisseur Semi-Flash.

De manière à limiter le nombre total de comparateurs, ces convertisseurs utilisent plusieurs étages flash de précision réduite (typiquement 3 ou 4 bits) chaînés. Chaque flash pilote un convertisseur numérique-analogique dont la sortie est soustraite au signal analogique d'entrée.

L'étage suivant code le résultat de la différence, améliorant ainsi la précision finale. Un convertisseur semi-flash effectue l'ensemble des opérations en un seul cycle d'horloge, ce qui limite sa vitesse au temps de propagation total le long de la chaîne.

En revanche, un convertisseur pipeline utilise un cycle d'horloge par étage. Ce séquencement nécessite un échantillonneur-bloqueur et un registre par étage mais permet d'être plus rapide puisque plusieurs échantillons sont traités simultanément.

Schéma de principe d'un convertisseur Pipeline.

Voir aussi

• Convertisseur numérique-analogique
• Échantillonnage (signal)
• Numérisation
• Quantification (signal)
• Serveur vidéo