Sirge ehk sirgjoon on ilma läbimõõduta, mõlemas suunas lõpmata pikk, kõverusteta joon ehk ühemõõtmeline ruum , mis võib sisalduda mitmemõõtmelises ruumis[ 1]
Sirge üldvõrrand tasandil on (Descartesi koordinaadistikus) ristkoordinaadistikus lineaarvõrrand
A
x
+
B
y
+
C
=
0
{\displaystyle Ax+By+C=0}
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
konstandid , kusjuures
A
{\displaystyle A}
B
{\displaystyle B}
Sirge võrrand tasandil:
4
x
−
1
y
−
1
=
0
ehk
y
=
4
x
−
1
{\displaystyle 4x-1y-1=0{\text{ ehk }}y=4x-1}
Kasutatakse üldvõrrandi
A
x
+
B
y
+
C
=
0
{\displaystyle Ax+By+C=0}
L
=
{
x
=
x
0
+
t
a
y
=
y
0
+
t
b
, kus
t
∈
R
{\displaystyle L=\left\{{\begin{array}{c}x=x_{0}+ta\\y=y_{0}+tb\end{array}}\right.{\text{, kus }}t\in \mathbb {R} }
[ 2] [ 3]
R
2
{\displaystyle \mathbb {R} ^{2}}
α
=
(
2
4
)
ja
β
=
(
3
3
)
{\displaystyle \alpha =\left({\begin{array}{c}2\\4\end{array}}\right){\text{ ja }}\beta =\left({\begin{array}{c}3\\3\end{array}}\right)}
L
=
a
+
t
(
β
−
α
→
)
,
kus
t
∈
R
=
(
2
+
t
4
−
t
)
,
kus
t
∈
R
{\displaystyle L={a+t({\overrightarrow {\beta -\alpha }}),{\text{ kus }}t\in \mathbb {R} }={\left({\begin{array}{c}2+t\\4-t\end{array}}\right),{\text{ kus }}t\in \mathbb {R} }}
või
L
=
b
+
t
(
β
−
α
→
)
,
kus
t
∈
R
=
(
3
+
t
3
−
t
)
,
kus
t
∈
R
{\displaystyle L={b+t({\overrightarrow {\beta -\alpha }}),{\text{ kus }}t\in \mathbb {R} }={\left({\begin{array}{c}3+t\\3-t\end{array}}\right),{\text{ kus }}t\in \mathbb {R} }}
Lisaks eelnimetatule on võimalik parameetrilist kuju tähistada, kui parameetrilisi võrrandeid
L
=
{
x
1
=
a
1
+
t
s
1
x
2
=
a
2
+
t
s
2
, kus
t
∈
R
=
{
x
1
=
3
+
t
x
2
=
3
−
t
, kus
t
∈
R
{\displaystyle L=\left\{{\begin{array}{c}x_{1}=a_{1}+ts_{1}\\x_{2}=a_{2}+ts_{2}\end{array}}\right.{\text{, kus }}t\in \mathbb {R} =\left\{{\begin{array}{c}x_{1}=3+t\\x_{2}=3-t\end{array}}\right.{\text{, kus }}t\in \mathbb {R} }
ja (Descartesi kujul) ehk kanoonilisel kujul
x
1
−
a
1
s
1
=
x
2
−
a
2
s
2
→
x
1
−
2
1
=
x
2
−
4
−
1
→
x
1
=
−
x
2
+
6
{\displaystyle {\frac {x_{1}-a_{1}}{s_{1}}}={\frac {x_{2}-a_{2}}{s_{2}}}\to {\frac {x_{1}-2}{1}}={\frac {x_{2}-4}{-1}}\to x_{1}=-x_{2}+6}
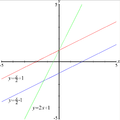
Võrrandiga
y
=
4
x
−
1
{\displaystyle y=4x-1}
määratud sirge.
Parameetrilise võrranditega
x
1
=
3
+
t
{\displaystyle x_{1}=3+t}
,
.
x
2
=
3
−
t
{\displaystyle .x_{2}=3-t}
määratud sirge.
Sirged tasandil.
Olgu antud sirged
u
{\displaystyle u}
v
{\displaystyle v}
s
→
1
{\displaystyle {\vec {s}}_{1}}
s
→
2
{\displaystyle {\vec {s}}_{2}}
Sirged on risti parajasti siis, kui nende sihivektorite tadamskalaarkorrutis on
0
{\displaystyle 0}
s
→
1
⋅
s
→
2
=
0
{\displaystyle {\vec {s}}_{1}\cdot {\vec {s}}_{2}=0}
Sirged on paralleelsed parajasti siis, kui nende sihivektorite skalaarkorrutise moodul on
1
{\displaystyle 1}
|
s
→
1
⋅
s
→
2
|
=
1
{\displaystyle |{\vec {s}}_{1}\cdot {\vec {s}}_{2}|=1}
Eukleidese geomeetrias läbib kahte eri punkti parajasti üks sirge.
Tõusu (k) ja algordinaadiga (a) määratud sirge võrrand tasandil:
y
=
k
x
+
a
{\displaystyle y=kx+a}
Kahe punktiga määratud sirge võrrand tasandil :
y
−
y
1
y
2
−
y
1
=
x
−
x
1
x
2
−
x
1
{\displaystyle {\frac {y-y_{1}}{y_{2}-y_{1}}}={\frac {x-x_{1}}{x_{2}-x_{1}}}}
Punkti ja sihivektoriga määratud sirge võrrand tasandil:
y
−
y
1
s
y
=
x
−
x
1
s
x
{\displaystyle {\frac {y-y_{1}}{s_{y}}}={\frac {x-x_{1}}{s_{x}}}}
Punkti ja tõusuga määratud sirge võrrand tasandil:
y
−
y
1
=
k
(
x
−
x
1
)
{\displaystyle y-y_{1}=k(x-x_{1})}
Kahe tasandi
Π
1
:
n
1
⋅
r
=
h
1
{\displaystyle \Pi _{1}:\mathbf {n} _{1}\cdot \mathbf {r} =h_{1}}
Π
2
:
n
2
⋅
r
=
h
2
{\displaystyle \Pi _{2}:\mathbf {n} _{2}\cdot \mathbf {r} =h_{2}}
n
i
{\displaystyle \mathbf {n} _{i}}
normaal vektor , on antud
r
=
(
c
1
n
1
+
c
2
n
2
)
+
λ
(
n
1
×
n
2
)
{\displaystyle \mathbf {r} =(c_{1}\mathbf {n} _{1}+c_{2}\mathbf {n} _{2})+\lambda (\mathbf {n} _{1}\times \mathbf {n} _{2})}
kus
c
1
=
h
1
−
h
2
(
n
1
⋅
n
2
)
1
−
(
n
1
⋅
n
2
)
2
{\displaystyle c_{1}={\frac {h_{1}-h_{2}(\mathbf {n} _{1}\cdot \mathbf {n} _{2})}{1-(\mathbf {n} _{1}\cdot \mathbf {n} _{2})^{2}}}}
c
2
=
h
2
−
h
1
(
n
1
⋅
n
2
)
1
−
(
n
1
⋅
n
2
)
2
.
{\displaystyle c_{2}={\frac {h_{2}-h_{1}(\mathbf {n} _{1}\cdot \mathbf {n} _{2})}{1-(\mathbf {n} _{1}\cdot \mathbf {n} _{2})^{2}}}.}
Olgu antud sirge
u
{\displaystyle u}
D
(
x
1
;
y
1
;
z
1
)
{\displaystyle D(x_{1};y_{1};z_{1})}
u
{\displaystyle u}
s
→
=
(
s
x
;
s
y
;
s
z
)
{\displaystyle {\overrightarrow {s}}=(s_{x};s_{y};s_{z})}
X
=
(
x
;
y
;
z
)
{\displaystyle X=(x;y;z)}
u
{\displaystyle u}
D
(
x
1
;
y
1
;
z
1
)
{\displaystyle D(x_{1};y_{1};z_{1})}
x
−
x
1
s
x
=
y
−
y
1
s
y
=
z
−
z
1
s
z
{\displaystyle {\frac {x-x_{1}}{s_{x}}}={\frac {y-y_{1}}{s_{y}}}={\frac {z-z_{1}}{s_{z}}}}
Siis leiame vektori
D
X
→
{\displaystyle {\overrightarrow {DX}}}
r
=
|
|
D
X
→
|
|
{\displaystyle r=\left|\left|{\overrightarrow {DX}}\right|\right|}
r
=
(
x
−
x
1
)
2
+
(
y
−
y
1
)
2
+
(
z
−
z
1
)
2
{\displaystyle r={\sqrt {\left(x-x_{1}\right){}^{2}+\left(y-y_{1}\right){}^{2}+\left(z-z_{1}\right){}^{2}}}}
Olgu antud sirged
u
{\displaystyle u}
v
{\displaystyle v}
s
1
→
{\displaystyle {\overrightarrow {s_{1}}}}
s
2
→
{\displaystyle {\overrightarrow {s_{2}}}}
A
{\displaystyle A}
B
{\displaystyle B}
ϱ
=
|
|
s
1
→
×
AB
→
|
|
|
|
s
1
→
|
|
{\displaystyle \varrho ={\frac {\left|\left|{\overrightarrow {s_{1}}}\times {\overrightarrow {\text{AB}}}\right|\right|}{\left|\left|{\overrightarrow {s_{1}}}\right|\right|}}}
ϱ
(
u
,
v
)
=
|
(
s
1
→
×
s
2
→
)
⋅
AB
→
|
|
|
s
1
→
×
s
2
→
|
|
{\displaystyle \varrho (u,v)={\frac {\left|({\overrightarrow {s_{1}}}\times {\overrightarrow {s_{2}}})\cdot {\overrightarrow {\text{AB}}}\right|}{\left|\left|{\overrightarrow {s_{1}}}\times {\overrightarrow {s_{2}}}\right|\right|}}}
y
−
y
1
=
(
f
′
(
x
)
)
(
x
−
x
1
)
{\displaystyle y-y_{1}={\frac {}{}}(f'(x))(x-x_{1})}
y
−
y
1
=
(
−
1
f
′
(
x
)
)
(
x
−
x
1
)
{\displaystyle y-y_{1}=\left({\frac {-1}{f'(x)}}\right)(x-x_{1})}
Võrrandiga määratud sirge.
Parameetrilise võrranditega , määratud sirge.
Sirged tasandil.
