Corrección de errores hacia adelante
En telecomunicaciones, teoría de la información y teoría de la codificación, la corrección de errores hacia adelante (en inglés, forward error correction o FEC) o codificación de canal[1][2] es una técnica utilizada para controlar los errores en la transmisión de datos a través de canales de comunicación poco fiables o ruidosos. La idea central es que el emisor codifica el mensaje de forma redundante, casi siempre utilizando un Código de corrección de errores (CCE). El mecanismo permite la corrección en el receptor sin retransmisión de la información original. Se utiliza en sistemas sin retorno o sistemas en tiempo real donde no se puede esperar a la retransmisión para mostrar los datos. Este mecanismo de corrección de errores se utiliza por ejemplo, en las comunicaciones vía satélite, en las grabadoras de DVD y CD o en las emisiones de TDT para terminales móviles (estándar DVB-H).
Principios generales
[editar]La protección contra errores es uno de los diversos elementos que forman el proceso de la radiodifusión digital.
La técnica consiste en una serie de modificaciones sobre la señal principal (los datos útiles) antes de ser transmitido que, una vez llega al receptor alterado por el ruido del canal, son decodificados y ayudan a detectar los errores y, por lo tanto, a minimizar a gran escala la tasa de errores por bit. Estas modificaciones se llevan a cabo en un orden determinado y a niveles de profundidad diferentes. De forma que al receptor se sigue el orden inverso para descodificar e ir corrigiendo errores hasta las capas superiores donde, finalmente, dispondremos de la señal original enviada por el emisor. A grandes rasgos, las modificaciones consisten en dos conceptos:[3]
- Sincronismo alto entre emisor y receptor.
- Redundancia a niveles de byte y de bit.
Los dos ayudan a reducir la tasa de errores de bit (BER, Bit error rate) en recepción.
Sincronismo
[editar]El sincronismo del receptor es un factor importante en la hora de mantener unas tasas de error de bit bajas. En radiodifusión de secuencias binarias (digital), los datos se envían según la modulación digital que se encuentre más adecuada (dependiente de las tasas de bit deseadas, el ancho de banda disponible, etc.). Dependiendo de esta modulación, cierto número de bits se agrupan en símbolos y todas las diferentes combinaciones posibles con este número de bits se mapeen en lo que se denomina constelación. El sincronismo no es otra cosa que el hecho que el receptor sepa con alta precisión donde empieza y dónde acaba cada símbolo (en qué instantes de tiempos). Por cada posible símbolo el emisor envía una señal diferenciable de los otros durante un tiempo que se denomina tiempo de símbolo. Cuando, después de un tiempo de símbolo, cambia la secuencia binaria que tenemos que enviar, vemos un cambio en la señal transmitida que se denomina transición. Cuando se da el caso donde se tiene que transmitir consecutivamente un mismo símbolo no hay transiciones durante cierto tiempo. La falta de transiciones perjudica la sincronización del receptor, por lo tanto, el que se hace a menudo en telecomunicaciones es forzar las transiciones de forma que, durante estos periodos donde se transmite el mismo, el receptor pueda mantener el sincronismo.
Un ejemplo bastante simple de una codificación que fuerce las transiciones es el código de marcas bifase (BMC-Biphaseal Mark Code, en inglés).
En el estándar de radiodifusión digital de televisión DVB, el bloque de protección contra errores (FEC) incluye un sistema que fuerza las transiciones para mantener el sincronismo del receptor: el aleatorizador.
Redundancia
[editar]La redundancia es la técnica que, junto con el sincronismo, se aplica antes de las transmisiones para proteger los datos contra errores. Esta técnica consiste a añadir información que ya existe en el paquete de datos (repetirla). El propósito de realizar esta redundancia de datos es promediar el ruido de canal. Si enviamos los datos sin redundancia, por cada elemento no podemos saber si en recepción el ruido tendrá un valor suficientmente bajo como para que el receptor lo pueda identificar como es debido. Sabiendo que el ruido es gaussiano de media cero, por lo tanto que sus valores más probables son próximos a cero, es poco probable que este sea bastante alto como para perjudicar al receptor en la hora de decidir el dato enviado.
Se tiene que decir, no obstante, que para hacer ciertas las premisas anteriores es necesario trabajar con unos parámetros de SNR (señal/ruido, signal to noise ratio, en inglés) mínimos. Esto significa que la potencia de la señal transmitida tiene que ser significativamente superior que la del ruido del canal, puesto que sino este perjudicaría el envío de datos no solo cuando tuviera unos valores altos (poco probable), sino también cuando tuviera valores medianos (muy probable), haciendo de la redundancia una técnica inútil. Asumiendo esta condición, si enviamos cada unidad de datos más de una vez, los valores que predominan serán casi unívocamente los que se hayan enviado realmente. Muchas veces cuando el ruido adquiere un valor alto, este perjudica a ráfagas de bits consecutivos hasta estabilizarse, por lo cual se aplican unas determinadas técnicas. Para hacer el proceso de detección-corrección de errores mediante redundancia se usan unos bloques en el emisor llamados codificadores y unos bloques en el receptor llamados descodificadores.
Funcionamiento
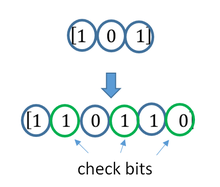
[editar]La posibilidad de corregir errores se consigue añadiendo al mensaje original unos bits de redundancia. La fuente digital envía la secuencia de datos al codificador, encargado de añadir dichos bits de redundancia. A la salida del codificador obtenemos la denominada palabra código. Esta palabra código es enviada al receptor y este, mediante el decodificador adecuado y aplicando los algoritmos de corrección de errores, obtendrá la secuencia de datos original. Los dos principales tipos de codificación usados son:
- Códigos bloque. La paridad en el codificador se introduce mediante un algoritmo algebraico aplicado a un bloque de bits. El decodificador aplica el algoritmo inverso para poder identificar y, posteriormente corregir los errores introducidos en la transmisión.
- Códigos convolucionales. Los bits se van codificando tal y como van llegando al codificador. Cabe destacar que la codificación de uno de los bits está enormemente influenciada por la de sus predecesores. La decodificación para este tipo de código es compleja ya que en principio, es necesaria una gran cantidad de memoria para estimar la secuencia de datos más probable para los bits recibidos. En la actualidad se utiliza para decodificar este tipo de códigos algoritmo de Viterbi, por su gran eficiencia en el consumo de recursos.
Ventajas
[editar]FEC reduce el número de transmisiones de errores, así como los requisitos de potencia de los sistemas de comunicación e incrementa la efectividad de los mismos evitando la necesidad del reenvío de los mensajes dañados durante la recepción.
Tipos
[editar]
Las dos categorías principales de códigos ECC son códigos de bloques y códigos convolucionales.
- Los códigos de bloque funcionan en bloques de tamaño fijo (paquetes) de bits o símbolos de tamaño predeterminado. Los códigos de bloque prácticos generalmente se pueden decodificar de forma rígida en tiempo polinomial a su longitud de bloque.
- Los códigos convolucionales funcionan en flujos de bits o símbolos de longitud arbitraria. La mayoría de las veces se decodifican de forma suave con el algoritmo de Viterbi, aunque a veces se usan otros algoritmos. La decodificación de Viterbi permite una eficiencia de decodificación asintóticamente óptima con una longitud de restricción creciente del código convolucional, pero a expensas de complejidad exponencialmente creciente. Un código convolucional terminado también es un "código de bloque" en el sentido de que codifica un bloque de datos de entrada, pero el tamaño del bloque de un código convolucional es generalmente arbitrario, mientras que los códigos de bloque tienen un tamaño fijo dictado por sus características algebraicas. Los tipos de terminación para códigos convolucionales incluyen "muerde la cola" y "descarga de bits".
Hay muchos tipos de códigos de bloque; Codificación Reed-Solomon es digno de mención por su uso generalizado en discos compacto, DVDs y unidades de disco duro. Otros ejemplos de códigos de bloque clásicos incluyen Golay, BCH, paridad multidimensional y código Hamming.
Hamming ECC se usa comúnmente para corregir errores de memoria NAND flash.[4] Esto proporciona corrección de errores de un solo bit y detección de errores de 2 bits. Los códigos Hamming solo son adecuados para células de un solo nivel (SLC) NAND más confiables. La célula de varios niveles (MLC) NAND más densa puede usar ECC de corrección de múltiples bits como BCH o Reed-Solomon.[5][6] NOR Flash normalmente no utiliza ninguna corrección de errores.[5]
Los códigos de bloque clásicos generalmente se decodifican utilizando algoritmos de decisión dura,[7] lo que significa que para cada señal de entrada y salida se toma una decisión dura si corresponde a un bit uno o cero. Por el contrario, los códigos convolucionales generalmente se decodifican utilizando algoritmos de decisión suave como los algoritmos de Viterbi, MAP o BCJR, que procesan señales analógicas (discretizadas) y que permiten un error mucho mayor y rendimiento de corrección que la decodificación de decisión dura.
Casi todos los códigos de bloque clásicos aplican las propiedades algebraicas de campos finitos. Por lo tanto, los códigos de bloque clásicos a menudo se denominan códigos algebraicos.
A diferencia de los códigos de bloque clásicos que a menudo especifican una capacidad de detección o corrección de errores, muchos códigos de bloque modernos como los códigos LDPC carecen de tales garantías. En cambio, los códigos modernos se evalúan en términos de sus tasas de error de bits.
La mayoría de los códigos de corrección de errores hacia adelante corrigen solo cambios de bits, pero no inserciones ni eliminaciones de bits. En esta configuración, la distancia de Hamming es la forma adecuada de medir la tasa de error de bits. Algunos códigos de corrección de errores de reenvío están diseñados para corregir inserciones y eliminaciones de bits, como códigos de marcador y códigos de marca de agua. La distancia de Levenshtein es una forma más apropiada de medir la tasa de error de bits cuando se utilizan dichos códigos.[8]
Tasa de código y la compensación entre confiabilidad y tasa de datos
[editar]El principio fundamental de ECC es agregar bits redundantes para ayudar al decodificador a encontrar el mensaje verdadero que fue codificado por el transmisor. La tasa de código de un sistema ECC dado se define como la relación entre el número de bits de información y el número total de bits (es decir, información más bits de redundancia) en un paquete de comunicación dado. La tasa de código es, por lo tanto, un número real. Una tasa de código baja cercana a cero implica un código fuerte que utiliza muchos bits redundantes para lograr un buen rendimiento, mientras que una tasa de código grande cercana a 1 implica un código débil.
Los bits redundantes que protegen la información deben transferirse utilizando los mismos recursos de comunicación que están tratando de proteger. Esto provoca una compensación fundamental entre la fiabilidad y la velocidad de datos.[9] En un extremo, un código fuerte (con baja tasa de código) puede inducir un aumento importante en la SNR (relación señal-ruido) del receptor, disminuyendo la tasa de error de bit, a costa de reducir la tasa de datos efectiva. En el otro extremo, no utilizar ningún ECC (es decir, una tasa de código igual a 1) utiliza el canal completo para la transferencia de información, a costa de dejar los bits sin protección adicional.
Una pregunta interesante es la siguiente: ¿qué tan eficiente en términos de transferencia de información puede ser un ECC que tiene una tasa de error de decodificación insignificante? Esta pregunta fue respondida por Claude Shannon con su segundo teorema, que dice que la capacidad del canal es la tasa de bits máxima alcanzable por cualquier ECC cuya tasa de error tiende a cero:[10] Su prueba se basa en la codificación aleatoria gaussiana, que no es adecuada para las aplicaciones del mundo real. El límite superior dado por el trabajo de Shannon inspiró un largo viaje en el diseño de ECC que pueden acercarse al límite máximo de rendimiento. Varios códigos hoy en día pueden alcanzar casi el límite de Shannon. Sin embargo, la capacidad de lograr los ECC suele ser extremadamente compleja de implementar.
Los ECC más populares tienen un equilibrio entre el rendimiento y la complejidad computacional. Por lo general, sus parámetros brindan un rango de posibles tasas de código, que se pueden optimizar según el escenario. Por lo general, esta optimización se realiza para lograr una baja probabilidad de error de decodificación y minimizar el impacto en la velocidad de datos. Otro criterio para optimizar la tasa de código es equilibrar la tasa de error baja y el número de retransmisiones con el fin de reducir el costo de energía de la comunicación.[11]
Promediando el ruido para reducir errores
[editar]Se podría decir que el CCE funciona "promediando el ruido"; dado que cada bit de datos afecta a muchos símbolos transmitidos, la corrupción de algunos símbolos por el ruido generalmente permite que los datos de usuario originales se extraigan de los otros símbolos recibidos no corruptos que también dependen de los mismos datos de usuario.
- Debido a este efecto de "reunión de riesgos", los sistemas de comunicación digital que utilizan CCE tienden a funcionar muy por encima de una cierta relación mínima de señal a ruido y nada por debajo de ella.
- Esta tendencia de todo o nada, denominada efecto acantilado, se vuelve más pronunciada a medida que se utilizan códigos más fuertes que se acercan más al límite teórico de Shannon.
- Intercalar datos codificados CCE puede reducir las propiedades de todo o nada de los códigos CCE transmitidos cuando los errores de canal tienden a ocurrir en ráfagas. Sin embargo, este método tiene límites; se utiliza mejor en datos de banda estrecha.
La mayoría de los sistemas de telecomunicaciones utilizan un código de canal fijo diseñado para tolerar la tasa de error de bit esperada en el peor de los casos y luego no funcionan si la tasa de error de bit es cada vez peor. Sin embargo, algunos sistemas se adaptan a las condiciones de error del canal dadas: algunas instancias de solicitud de repetición automática híbrida usan un método CCE fijo siempre que el CCE pueda manejar la tasa de error, luego cambian a ARQ cuando la tasa de error es demasiado alta; la modulación y la codificación adaptables utilizan una variedad de tasas de CCE, agregando más bits de corrección de errores por paquete cuando hay tasas de error más altas en el canal, o eliminándolos cuando no son necesarios.
Compromisos
[editar]En general incluir un número mayor de bits de redundancia supone una mayor capacidad para corregir errores. Sin embargo, este hecho reduce notablemente el régimen binario de transmisión, y aumenta el retardo en la recepción del mensaje
Referencias
[editar]- ↑ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink (The Aerospace Corporation) 3 (1). Archivado desde el original el 25 de febrero de 2012. Consultado el 5 de marzo de 2006. «How Forward Error-Correcting Codes Work».
- ↑ Maunder, Robert (2016). «Overview of Channel Coding».
- ↑ Constantino Pérez Vega Codificación de Canal
- ↑ "Hamming codes for NAND flash memory devices" Archivado el 21 de agosto de 2016 en Wayback Machine.. EE Times-Asia. Apparently based on "Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices" Archivado el 29 de agosto de 2017 en Wayback Machine.. 2005. Both say: "The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications."
- ↑ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011. «Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash.... Hamming based block codes are the most commonly used ECC for SLC.... both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.»
- ↑ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory». p. 28. «For SLC, a code with a correction threshold of 1 is sufficient. t=4 required... for MLC.»
- ↑ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting 2008: 1-12. doi:10.1155/2008/957846.
- ↑ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Consultado el 20 de diciembre de 2018.
- ↑ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK.
- ↑ Shannon, C. E. (1948). «A mathematical theory of communication». Bell System Technical Journal 27 (3–4): 379-423 & 623-656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ↑ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775-780. ISBN 978-1-4799-3083-8. doi:10.1109/WCNC.2014.6952166.
