Efecto Hall
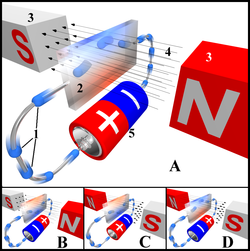
Leyenda:
1. Electrones
2. Sensor o sonda Hall
3. Imanes
4. Campo magnético
5. Fuente de energía
Descripción:
En la imagen A, una carga negativa aparece en el borde superior del sensor Hall (simbolizada con el color azul), y una positiva en el borde inferior (color rojo). En B y C, el campo eléctrico o el magnético están invertidos, causando que la polaridad se invierta. Invertir tanto la corriente como el campo magnético (imagen D) causa que la sonda asuma de nuevo una carga negativa en la esquina superior.

Se conoce como efecto Hall a la aparición de un campo eléctrico por separación de cargas en el interior de un conductor por el que circula una corriente en presencia de un campo magnético[1] con componente perpendicular al movimiento de las cargas. Este campo eléctrico (campo Hall) es perpendicular al movimiento de las cargas y a la componente perpendicular del campo magnético aplicado. Lleva el nombre de su primer modelador, el físico estadounidense Edwin Herbert Hall (1855-1938).
En épocas contemporáneas (1985), el físico alemán Klaus von Klitzing y sus colaboradores descubrieron el hoy conocido como efecto Hall cuántico, lo que les valió la obtención del premio Nobel de Física en 1985. En 1998 se otorgó un nuevo premio Nobel de Física a los profesores Laughlin, Strömer y Tsui por el descubrimiento de un nuevo fluido cuántico con excitaciones de carga fraccionarias. Este nuevo efecto ha traído grandes problemas a los físicos teóricos y actualmente constituye uno de los campos de investigación de mayor interés y actualidad en toda la física del estado sólido.
Explicación cualitativa del efecto Hall clásico
[editar]Cuando por un material conductor o semiconductor circula una corriente eléctrica, y estando este mismo material en el seno de un campo magnético, se comprueba que aparece una fuerza magnética en los portadores de carga que los reagrupa dentro del material; esto es, los portadores de carga se desvían y agrupan a un lado del material conductor o semiconductor, apareciendo así una variación de potencial en el conductor, lo cual origina un campo eléctrico perpendicular al campo magnético y al propio campo eléctrico generado por la batería (). Este campo eléctrico es el denominado campo Hall (), y ligada a él aparece la tensión Hall, que se puede medir mediante el voltímetro de la figura.
En el caso de la figura, se tiene una barra de un material desconocido y se quiere saber cuáles son sus portadores de carga. Para ello, mediante una batería se hace circular por la barra una corriente eléctrica. Una vez hecho esto, se introduce la barra en el seno de un campo magnético uniforme y perpendicular a la tableta.
Aparecerá entonces una fuerza magnética sobre los portadores de carga, que tenderá a agruparlos a un lado de la barra, apareciendo de este modo una tensión Hall y un campo eléctrico Hall entre ambos lados de la barra. Dependiendo de si la lectura del voltímetro es positiva o negativa, y conociendo la dirección del campo magnético y del campo eléctrico originado por la batería, se puede deducir si los portadores de carga de la barra de material desconocido son las cargas positivas o las negativas.
En la figura de al lado se ve cómo el material tiene dos zonas: la de la izquierda y la de la derecha. En una zona, los portadores son huecos y en la otra electrones.
Explicación cuantitativa del efecto Hall clásico
[editar]Sea el material por el que circula la corriente con una velocidad v al que se le aplica un campo magnético B. Al aparecer una fuerza magnética , los portadores de carga se agrupan en una región del material, ocasionando la aparición de una tensión y por lo tanto de un campo eléctrico E en la misma dirección. Este campo ocasiona a su vez la aparición de una fuerza eléctrica de dirección contraria a .
Formalismo matricial en un sistema 2D
[editar]Dado un sistema conductor bidimensional en el plano xy con un campo magnético a lo largo de z como el mostrado en la figura de abajo, el voltaje Hall se puede derivar utilizando la Fuerza de Lorentz.
donde es la masa efectiva de portadores (electrones) dentro del sólido, el tiempo entre las colisiones de los electrones con los iones en el sólido (modelo de Drude) y v la velocidad de deriva.
La ecuación anterior se puede reorganizar como el siguiente sistema matricial
Del electromagnetismo clásico, la expresión para la densidad de la corriente es ,[2] siendo n la densidad de electrones por unidad de área, q la carga eléctrica y σ el tensor de conductancia, que está relacionado con la resistividad de la siguiente forma ρ = 1⁄σ. Usando estas definiciones, el campo eléctrico se relaciona con la densidad de corriente por la resistividad de la siguiente manera
donde y

En la condición de estado estacionario, las cargas no se mueven en la dirección del eje y, ya que la fuerza magnética en cada electrón en la dirección del eje y se cancela por una fuerza eléctrica del eje y debido a la acumulación de cargas. Por lo tanto, la corriente en la dirección del eje y se cancela Jy = 0 y las expresiones para el campo eléctrico terminan siendo
Ex = ρxxJx
Ey = ρxyJx
donde ya que el sistema considerado es 2D.
En el experimento, los voltajes medidos son
Vx = ExL = ρxx IxL/W = RxxIx
Vy = VH = EyW = ρxy Ix = RyxIx = RHIx
donde R es la resistencia dada por Ley de Ohm.
A partir de la medida de VH uno puede determinar la densidad de portadores, ya que y de Vx se puede obtener la movilidad de cargas
La física clásica del efecto Hall
[editar]Se sabe que un campo magnético actúa sobre las cargas en movimiento (fuerza de Lorentz).
Una corriente I que atraviesa un material consiste en cargas (electrones) que se desplazan (en dirección contraria a la corriente) con una velocidad que se denomina v. Si se sumerge esa corriente de electrones en un campo magnético B, cada uno de los electrones que forman la corriente estará sometidos a la fuerza de Lorenz Fm = -e.v^B (como en el dibujo se cambió la dirección de v, ya que se está considerando un electrón, no debería considerarse el signo negativo de la carga). Donde -e corresponde a la carga de un electrón, v el vector velocidad del electrón y B el vector campo magnético aplicado.

La dirección de la fuerza será perpendicular al plano formado por v y B (ya que es resultado del producto vectorial de ambos) y provocará un desplazamiento de electrones en esa dirección.
Como consecuencia se tendrá una concentración de cargas negativas sobre uno de los lados del material y un déficit de cargas negativas en el lado opuesto. Esta distribución de cargas genera una diferencia de potencial entre ambos lados, la tensión de Hall VH, y un campo eléctrico EH.
Este campo eléctrico que genera a su vez una fuerza eléctrica sobre los electrones dada por la ley de Coulomb, Fe = -e . EH, que actúa en dirección contraria que la fuerza de Lorentz. El equilibrio se alcanzará cuando la suma de las dos, de lo cual se deduce que en el equilibrio el valor del campo Hall es: EH = -v×B.
Técnicas de medición
[editar]Sin duda, la técnica de medición más utilizada para la determinación de los portadores de carga y resistividad en un semiconductor es la técnica de Van Der Paw. Es conocida también como técnica de cuatro puntas.
Aplicaciones
[editar]El uso de sensores de Efecto Hall permite medir la movilidad de una partícula cargada eléctricamente (electrones, lagunas, etc.), así como los campos magnéticos (teslámetros) o la intensidad de corrientes eléctricas (sensores de corriente de efecto Hall). Este tipo de sensor evita el desgaste que sufren los contactos eléctricos tradicionales, y por ende es utilizado en la elaboración de sensores o detectores de posición sin contacto, por ejemplo en automóviles para detectar la posición de un árbol giratorio (árbol de levas, caja de cambios, paliers, etc.), y bajo las teclas de instrumentos de música modernos (órganos, órganos digitales, sintetizadores). También se utilizan en el codificador de motores de corriente continua.
Los motores de Efecto Hall (HET) son aceleradores de plasma de gran eficacia.[cita requerida]
Referencias
[editar]- ↑ Zabala, Gonzalo (2007). Robotica. USERSHOP. ISBN 9789871347568. Consultado el 12 de marzo de 2018.
- ↑ The Physics of Low-dimensional Semiconductors.An Introduction, John H.Davies. ISBN 9780511819070
Véase también
[editar]Enlaces externos
[editar] Wikimedia Commons alberga una galería multimedia sobre Efecto Hall.
Wikimedia Commons alberga una galería multimedia sobre Efecto Hall.
Efecto Hall descubierto por Edwin Hall
[editar]- Stormer, Horst L., Nobel lecture: the fractional quantum Hall effect (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última)., Review of Modern Physics, 71, 4, 1999, 875-889 (en inglés)
- física del efecto hall

















