36edo

← 35edo

36edo

37edo →

Prime factorization	22 × 32
Step size	33.3333¢
Fifth	21\36 (700¢) (→7\12)
Semitones (A1:m2)	3:3 (100¢ : 100¢)
Consistency limit	7
Distinct consistency limit	7
Special properties	Highly composite

English Wikipedia has an article on:

Sixth tone

36 equal divisions of the octave (abbreviated 36edo or 36ed2), also called 36-tone equal temperament (36tet) or 36 equal temperament (36et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 36 equal parts of about 33.3 ¢ each. Each step represents a frequency ratio of 2^1/36, or the 36th root of 2.

Theory

Since 36 is divisible by 12, it contains the overly-familiar 12edo as a subset. It divides 12edo's 100-cent half step into three microtonal steps of approximately 33 cents, which could be called "sixth tones." 36edo also contains 18edo ("third tones") and 9edo ("two-thirds tones") as subsets, not to mention the 6edo whole tone scale, 4edo full-diminished seventh chord, and the 3edo augmented triad, all of which are present in 12edo.

That 36edo contains 12edo as a subset makes it compatible with traditional instruments tuned to 12edo. By tuning one 12-edo instrument up or down about 33 cents, one can arrive at a 24-tone subset of 36 edo (see, for instance, Jacob Barton's piece for two clarinets, De-quinin' ^{[dead link]}). Three 12edo instruments could play the entire gamut.

In the 5-limit, 36edo offers no improvement over 12edo, since its nearest approximation to 5:4 is the overly-familiar 400-cent major third. However, it excels at the 7th harmonic and intervals involving 7. As a 3 and 7 tuning, or in other words as a tuning for the 2.3.7 just intonation subgroup, 36edo's single degree of around 33 cents serves a double function as 49:48, the so-called Slendro diesis of around 36 cents, and as 64:63, the so-called septimal comma of around 27 cents. Meanwhile, its second degree functions as 28:27, the so-called Septimal third-tone (which = 49:48 x 64:63). The 2.3.7 subgroup can be extended to the 2*36 subgroup 2.3.25.7.55.13.17, and on this subgroup it tempers out the same commas as 72edo does in the full 17-limit.

36edo also offers a good approximation to the acoustic golden ratio, as 25\36.

The 36edo patent val, like 12, tempers out 81/80, 128/125 and 648/625 in the 5-limit. It departs from 12 in the 7-limit, tempering out 686/675, and as a no-fives temperament, 1029/1024 and 118098/117649. The no-fives temperament tempering out 1029/1024, slendric, is well supported by 36edo, its generator of ~8/7 represented by 7 steps of 36edo. In the 11-limit, the patent val tempers out 56/55, 245/242 and 540/539, and is the optimal patent val for the rank four temperament tempering out 56/55, as well as the rank three temperament melpomene tempering out 81/80 and 56/55. In the 13-limit, it tempers out 78/77, in the 17-limit 51/50, and in the 19-limit 76/75, 91/90 and 96/95.

As a 5-limit temperament, the patent val for 36edo is contorted, meaning there are notes of it which cannot be reached from the unison using only 5-limit intervals. A curious alternative val for the 5-limit is ⟨36 65 116], which is not contorted. It is also a meantone val, in the sense that 81/80 is tempered out. However, the "comma" [29 0 -9⟩ is also tempered out, and the "fifth", 29\36, is actually approximately 7/4, whereas the "major third", 44\36, is actually approximately 7/3. Any 5-limit musical piece or scale which is a transversal for a meantone piece or scale will be converted to a no-fives piece tempering out 1029/1024 in place of 81/80 by applying this val.

Another 5-limit alternative val is ⟨36 57 83] (36c-edo), which is similar to the patent val but has 5/4 mapped to the 367-cent submajor third rather than the major third. This mapping supports very sharp porcupine temperament using 5\36 as a generator.

Heinz Bohlen proposed 36edo as a suitable temperament for approximating his 833-cents scale. The 13th harmonic (octave reduced) is so closely mapped on acoustic phi that 36edo could be treated as a 2.3.7.ϕ.17 temperament.

Prime harmonics

Approximation of prime harmonics in 36edo

Harmonic		2	3	5	7	11	13	17	19	23	29	31
Error	Absolute (¢)	+0.00	-1.96	+13.69	-2.16	+15.35	-7.19	-4.96	+2.49	+5.06	+3.76	-11.70
	Relative (%)	+0.0	-5.9	+41.1	-6.5	+46.0	-21.6	-14.9	+7.5	+15.2	+11.3	-35.1
Steps (reduced)		36 (0)	57 (21)	84 (12)	101 (29)	125 (17)	133 (25)	147 (3)	153 (9)	163 (19)	175 (31)	178 (34)

Divisors

36edo is the 7th highly composite EDO, with subset edos 1, 2, 3, 4, 6, 9, 12, 18.

Intervals

Degree	Cents	Approximate ratios of 2.3.7	Additional ratios of 2.3.7.13.17.19	Additional ratios of 2.3.5.7	Ups and downs notation
0	0.00	1/1			P1	perfect unison	D
1	33.33	64/63, 49/48			^1	up unison	^D
2	66.67	28/27			vm2	downminor 2nd	vEb
3	100	256/243	17/16, 18/17	16/15	m2	minor 2nd	Eb
4	133.33	243/224	14/13, 13/12		^m2	upminor 2nd	^Eb
5	166.67	54/49			vM2	downmajor 2nd	vE
6	200	9/8	19/17	10/9	M2	major 2nd	E
7	233.33	8/7			^M2	upmajor 2nd	^E
8	266.67	7/6			vm3	downminor 3rd	vF
9	300	32/27	19/16	6/5	m3	minor 3rd	F
10	333.33	98/81	17/14		^m3	upminor 3rd	^F
11	366.67	243/196	16/13, 26/21, 21/17		vM3	downmajor 3rd	vF#
12	400	81/64	24/19	5/4, 32/25	M3	major 3rd	F#
13	433.33	9/7			^M3	upmajor 3rd	^F#
14	466.67	64/49, 21/16	17/13		v4	down 4th	vG
15	500.00	4/3			P4	4th	G
16	533.33	49/36			^4	up 4th	^G
17	566.67		18/13	7/5	vA4	downaug 4th	vG#
18	600		17/12, 24/17	45/32, 64/45	A4, d5	aug 4th, dim 5th	G#, Ab
19	633.33		13/9	10/7	^d5	updim 5th	^Ab
20	666.67	72/49			v5	down 5th	vA
21	700	3/2			P5	5th	A
22	733.33	49/32, 32/21	26/17		^5	up fifth	^A
23	766.67	14/9			vm6	downminor 6th	vBb
24	800	128/81	19/12	8/5, 25/16	m6	minor 6th	Bb
25	833.33	392/243	13/8, 21/13, 34/21		^m6	upminor 6th	^Bb
26	866.67	81/49	28/17		vM6	downmajor 6th	vB
27	900	27/16	32/19	5/3	M6	major 6th	B
28	933.33	12/7			^M6	upmajor 6th	^B
29	966.67	7/4			vm7	downminor 7th	vC
30	1000	16/9	34/19	9/5	m7	minor 7th	C
31	1033.33	49/27			^m7	upminor 7th	^C
32	1066.67	448/243	13/7, 24/13		vM7	downmajor 7th	vC#
33	1100	243/128	32/17, 17/9	15/8	M7	major 7th	C#
34	1133.33	27/14			^M7	upmajor 7th	^C#
35	1166.67	63/32, 96/49			v8	down 8ve	vD
36	1200.00	2/1			P8	8ve	D

Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See Ups and Downs Notation - Chords and Chord Progressions.

Notation

Colored notes

One way of notating 36edo (at least for people who aren't colorblind) is to use colors. For example,  A  is 331⁄3 cents below  A  and  A  is 331⁄3 cents above  A . Or, the colors could be written out (red A, blue C♯, etc.) or abbreviated as rA, bC♯, etc. This use of red and blue is consistent with color notation (ru and zo).

Ups and downs notation

Another way to notate the microtonal notes which doesn't rely on colors is to use ups and downs. Here, this can be done using sharps and flats with arrows, borrowed from extended Helmholtz–Ellis notation:

Semitones	0	1⁄3	2⁄3	1	1+1⁄3	1+2⁄3	2	2+1⁄3
Sharp Symbol
Flat Symbol

If the arrows are taken to have their own layer of enharmonic spellings, then in some cases notes may be best denoted using double arrows.

Relation to 12edo and other tunings

For people accustomed to 12edo, 36edo is one of the easiest (if not the easiest) higher edo to become accustomed to. This is because one way to envision it is as an extended 12edo to which blue notes (which are a sixth-tone lower than normal) and "red notes" (a sixth-tone higher) have been added.

The intervals in 36edo are all either the familiar 12edo intervals, or else "red" and "blue" versions of them. Unlike 24edo, which has genuinely foreign intervals such as 250 cents (halfway between a tone and a third) and 450 cents (halfway between a fourth and a third), the new intervals in 36edo all variations on existing ones. Unlike 24edo, 36edo is also relatively free of what Easley Blackwood called "discordant" intervals. The 5th and 11th harmonics fall almost halfway in between scale degrees of 36edo, and thus intervals containing them can be approximated two different ways, one of which is significantly sharp and the other significantly flat. The 333.333-cent interval (the "red minor third") sharply approximates 6/5 and flatly approximates 11/9, for instance, whereas the sharp 11/9 is 366.667 cents and the flat 6/5 is 300 cents. However, 11/10, 20/11, 15/11, and 22/15 all have accurate and consistent approximations since the errors on the 5th and 11th harmonics cancel out with both tending sharp.

36edo is fairly cosmopolitan because many genres of world music can be played in it. Because of the presence of blue notes, and the closeness with which the 7th harmonic and its intervals are matched, 36edo is an ideal scale to use for African-American genres of music such as blues and jazz, in which septimal intervals are frequently encountered. Indonesian gamelan music using pelog easily adapts to it as well, since 9edo is a subset and can be notated as every fourth note, and Slendro can be approximated in several different ways as well. 36edo can therefore function as a "bridge" between these genres and Western music. Arabic and Persian music do not adapt as well, however, since their microtonal intervals consist of mostly quarter tones.

The "red unison" and "blue unison" are in fact the same interval (33.333 cents), which is actually fairly consonant as a result of being so narrow (it is perceived as a unison, albeit noticeably "out of tune", but still not overly unpleasant). In contrast, most people consider 24edo's 50 cent step to sound much more discordant when used as a subminor second.

People with perfect (absolute) pitch often have a difficult time listening to xenharmonic and non-12edo scales, which is due to their ability to memorize and become accustomed to the pitches and intervals of 12edo resulting in other pitches and intervals sounding out of tune. This is not as much of a problem with 36edo, due to its similarity to 12. With practice, it might even be possible to extend one's perfect pitch to be able to recognize blue and red notes.

"Quark"

In particle physics, baryons, which are the main building blocks of atomic nuclei, are always comprised of three quarks. One could draw an analogy between baryons and semitones (the main building block of 12edo); the baryon is comprised of three quarks and the semitone of three sixth-tones. The number of quarks in a colorless particle is always a multiple of three; similarly, the width of "colorless" intervals (the 12-edo intervals, which are neither red nor blue), expressed in terms of sixth-tones, is always a multiple of three. Because of this amusing coincidence, Mason Green proposes referring to the 33.333-cent sixth-tone interval as a "quark".

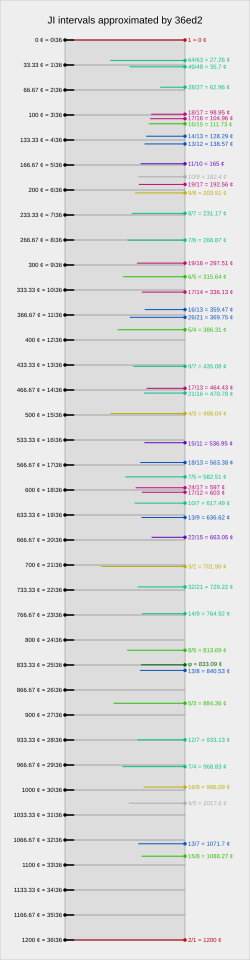
JI approximation

Selected 29-limit intervals approximated in 36edo

Interval mappings

The following tables show how 15-odd-limit intervals are represented in 36edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 36edo (direct approximation, even if inconsistent)

Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
7/6, 12/7	0.204	0.6
11/10, 20/11	1.662	5.0
9/7, 14/9	1.751	5.3
3/2, 4/3	1.955	5.9
7/4, 8/7	2.159	6.5
13/9, 18/13	3.284	9.9
15/11, 22/15	3.617	10.9
9/8, 16/9	3.910	11.7
13/7, 14/13	5.035	15.1
13/12, 24/13	5.239	15.7
13/8, 16/13	7.194	21.6
13/11, 22/13	10.790	32.4
15/8, 16/15	11.731	35.2
13/10, 20/13	12.453	37.4
5/4, 8/5	13.686	41.1
15/14, 28/15	13.891	41.7
11/9, 18/11	14.075	42.2
15/13, 26/15	14.408	43.2
11/8, 16/11	15.349	46.0
5/3, 6/5	15.641	46.9
9/5, 10/9	15.737	47.2
11/7, 14/11	15.825	47.5
7/5, 10/7	15.846	47.5
11/6, 12/11	16.030	48.1

15-odd-limit intervals in 36edo (patent val mapping)

Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
7/6, 12/7	0.204	0.6
11/10, 20/11	1.662	5.0
9/7, 14/9	1.751	5.3
3/2, 4/3	1.955	5.9
7/4, 8/7	2.159	6.5
13/9, 18/13	3.284	9.9
15/11, 22/15	3.617	10.9
9/8, 16/9	3.910	11.7
13/7, 14/13	5.035	15.1
13/12, 24/13	5.239	15.7
13/8, 16/13	7.194	21.6
15/8, 16/15	11.731	35.2
5/4, 8/5	13.686	41.1
15/14, 28/15	13.891	41.7
11/8, 16/11	15.349	46.0
5/3, 6/5	15.641	46.9
7/5, 10/7	15.846	47.5
11/6, 12/11	17.304	51.9
11/7, 14/11	17.508	52.5
9/5, 10/9	17.596	52.8
15/13, 26/15	18.926	56.8
11/9, 18/11	19.259	57.8
13/10, 20/13	20.881	62.6
13/11, 22/13	22.543	67.6

3-limit (Pythagorean) approximations (same as 12edo):

3/2 = 701.955... cents; 21 degrees of 36edo = 700 cents.

4/3 = 498.045... cents; 15 degrees of 36edo = 500 cents.

9/8 = 203.910... cents; 6 degrees of 36edo = 200 cents.

16/9 = 996.090... cents; 30 degrees of 36edo = 1000 cents.

27/16 = 905.865... cents; 27 degrees of 36edo = 900 cents.

32/27 = 294.135... cents; 9 degrees of 36edo = 300 cents.

81/64 = 407.820... cents; 12 degrees of 36edo = 400 cents.

128/81 = 792.180... cents; 24 degrees of 36edo = 800 cents.

7-limit approximations:

7 only:

7/4 = 968.826... cents; 29 degrees of 36edo = 966.666... cents.

8/7 = 231.174... cents; 7 degrees of 36edo = 233.333... cents.

49/32 = 737.652... cents; 22 degrees of 36edo = 733.333... cents.

64/49 = 462.348... cents; 14 degrees of 36edo = 466.666... cents.

3 and 7:

7/6 = 266.871... cents; 8 degrees of 36edo = 266.666... cents.

12/7 = 933.129... cents; 28 degrees of 36 = 933.333... cents.

9/7 = 435.084... cents; 13 degrees of 36edo = 433.333... cents.

14/9 = 764.916... cents; 23 degrees of 36edo = 766.666... cents.

28/27 = 62.961... cents; 2 degrees of 36edo = 66.666... cents.

27/14 = 1137.039... cents; 34 degrees of 36edo = 1133.333... cents.

21/16 = 470.781... cents; 14 degrees of 36edo = 466.666... cents.

32/21 = 729.219... cents; 22 degrees of 36edo = 733.333... cents.

49/48 = 35.697... cents; 1 degree of 36edo = 33.333... cents.

96/49 = 1164.303... cents; 35 degrees of 36edo = 1166.666... cents.

49/36 = 533.742... cents; 16 degrees of 36edo = 533.333... cents.

72/49 = 666.258... cents; 20 degrees of 36edo = 666.666... cents.

64/63 = 27.264... cents; 1 degree of 36edo = 33.333... cents.

63/32 = 1172.736... cents; 35 degrees of 36edo = 1166.666... cents.

Regular temperament properties

Subgroup	Comma List	Mapping	Optimal 8ve Stretch (¢)	Tuning Error
				Absolute (¢)	Relative (%)
2.3.7	1029/1024, 177147/175616	[⟨36 57 101]]	+0.67	0.51	1.53
2.3.7.13	729/728, 1029/1024, 3159/3136	[⟨36 57 101 133]]	+0.99	0.71	2.12
2.3.7.13.17	273/272, 729/728, 833/832, 3159/3136	[⟨36 57 101 133 147]]	+1.03	0.64	1.92
2.3.7.13.17.19	153/152, 273/272, 442/441, 729/728, 1729/1728	[⟨36 57 101 133 147 153]]	+0.76	0.84	2.52
2.3.5.7	81/80, 128/125, 686/675	[⟨36 57 84 101]]	−0.98	2.87	8.63
2.3.5.7.13	81/80, 91/90, 128/125, 169/168	[⟨36 57 84 101 133]]	−0.40	2.82	8.47
2.3.5.7.13.17	51/50, 81/80, 91/90, 128/125, 196/195	[⟨36 57 84 101 133 147]]	−0.13	2.65	7.94
2.3.5.7.13.17.19	51/50, 76/75, 81/80, 91/90, 96/95, 196/195	[⟨36 57 84 101 133 147 153]]	−0.19	2.45	7.36

Commas

This is a partial list of the commas that 36edo tempers out with its patent val, ⟨36 57 84 101 125 133].

Prime Limit	Ratio	Monzo	Cents	Color name	Name(s)
3	(12 digits)	[-19 12⟩	23.46	Lalawa	Pythagorean comma
5	648/625	[3 4 -4⟩	62.57	Quadgu	Greater diesis, diminished comma
5	(12 digits)	[18 -4 -5⟩	60.61	Saquingu	Passion comma
5	128/125	[7 0 -3⟩	41.06	Trigu	Lesser diesis, augmented comma
5	81/80	[-4 4 -1⟩	21.51	Gu	Syntonic comma, Didymus comma, meantone comma
5	2048/2025	[11 -4 -2⟩	19.55	Sagugu	Diaschisma
5	(16 digits)	[26 -12 -3⟩	17.60	Sasa-trigu	Misty comma
5	32805/32768	[-15 8 1⟩	1.95	Layo	Schisma
5	(98 digits)	[161 -84 -12⟩	0.02	Sepbisa-quadbigu	Kirnberger's atom
7	1029/1000	[-3 1 -3 3⟩	49.49	Trizogu	Keega
7	686/675	[1 -3 -2 3⟩	27.99	Trizo-agugu	Senga
7	1728/1715	[6 3 -1 -3⟩	13.07	Triru-agu	Orwellisma
7	(14 digits)	[21 -5 -2 -3⟩	11.12	Satriru-agugu	Bronzisma
7	1029/1024	[-10 1 0 3⟩	8.43	Latrizo	Gamelisma
7	10976/10935	[5 -7 -1 3⟩	6.48	Satrizo-agu	Hemimage comma
7	(20 digits)	[31 -6 -2 -6⟩	2.69	Sasa-tribiru-agugu	Pessoalisma
7	(16 digits)	[-11 -9 0 9⟩	1.84	Tritrizo	Septimal ennealimma
11	56/55	[3 0 -1 1 -1⟩	31.19	Luzogu	Undecimal tritonic comma
11	1350/1331	[1 3 2 0 -3⟩	24.54	Trilu-ayoyo	Large Tetracot diesis
11	245/242	[-1 0 1 2 -2⟩	21.33	Luluzozoyo	Frostma
11	176/175	[4 0 -2 -1 1⟩	9.86	Lorugugu	Valinorsma
11	896/891	[7 -4 0 1 -1⟩	9.69	Saluzo	Pentacircle comma
11	540/539	[2 3 1 -2 -1⟩	3.21	Lururuyo	Swetisma
11	4000/3993	[5 -1 3 0 -3⟩	3.03	Triluyo	Wizardharry comma, pine comma
11	9801/9800	[-3 4 -2 -2 2⟩	0.18	Bilorugu	Kalisma, Gauss' comma
13	78/77	[1 1 0 -1 -1 1⟩	22.34	Tholuru	Negustma
13	91/90	[-1 -2 -1 1 0 1⟩	19.13	Thozogu	Superleap comma, biome comma
13	144/143	[4 2 0 0 -1 -1⟩	12.06	Thulu	Grossma
13	169/168	[-3 -1 0 -1 0 2⟩	10.27	Thothoru	Buzurgisma, dhanvantarisma
13	196/195	[2 -1 -1 2 0 -1⟩	8.86	Thuzozogu	Mynucuma
13	2197/2187	[0 -7 0 0 0 3⟩	7.90	Satritho	Threedie comma
13	2080/2079	[5 -3 1 -1 -1 1⟩	0.83	Tholuruyo	Ibnsinma, sinaisma
13	4096/4095	[12 -2 -1 -1 0 -1⟩	0.42	Sathurugu	Schismina
17	51/50	[-1 1 -2 0 0 0 1⟩	34.28	Sogugu	Large septendecimal sixth tone
17	136/135	[3 -3 -1 0 0 0 1⟩	12.78	Sogu	Diatisma, fiventeen comma
17	256/255	[8 -1 -1 0 0 0 -1⟩	6.78	Sugu	Charisma, septendecimal kleisma
17	273/272	[-4 1 0 1 0 1 -1⟩	6.35	Suthozo	Tannisma
17	289/288	[-5 -2 0 0 0 0 2⟩	6.00	Soso	Semitonisma
19	76/75	[2 -1 -2 0 0 0 0 1⟩	22.93	Nogugu	Large undevicesimal ninth tone
19	96/95	[5 1 -1 0 0 0 0 -1⟩	18.13	Nugu	19th Partial chroma
19	133/132	[-2 -1 0 1 -1 0 0 1⟩	13.07	Noluzo	Minithirdma
19	153/152	[-3 2 0 0 0 0 1 -1⟩	11.35	Nuso	Ganassisma
19	171/170	[-1 2 -1 0 0 0 -1 1⟩	10.15	Nosugu	Malcolmisma
19	324/323	[2 4 0 0 0 0 -1 -1⟩	5.35	Nusu	Photisma
19	361/360	[-3 -2 -1 0 0 0 0 2⟩	4.80	Nonogu	Go comma

Rank-2 temperaments

Periods per 8ve	Generator (Reduced)	Cents (Reduced)	Associated Ratio (Reduced)	Temperament	MoS Scales
1	5\36	166.667	10/9	Squirrel (36), Porcupine (36c)	1L 6s, 7L 1s, 7L 8s, 7L 15s, 7L 22s
	7\36	233.333	8/7	Slendric, Mothra, Guiron	1L 4s, 1L 5s, 5L 1s, 5L 6s, 5L 11s, 5L 16s, 5L 21s, 5L 26s
	11\36 (25/36)	366.66 (833.33)	φ		3L 1s, 3L 4s, 3L 7s, 10L 3s, 13L 10s
	13\36	433.333	9/7		2L 1s, 3L 2s, 3L 5s, 3L 8s, 11L 3s, 11L 14s
	17\36	566.667	7/5	Liese, Pycnic	2L 1s, 2L 3s, 2L 5s, 2L 7s, 2L 9s ... 2L 15s, 17L 2s
2	5\36	166.667	10/9	Echidna, Hedgehog	2L 4s, 6L 2s, 8L 6s, 14L 8s
	7\36	233.333	8/7	Baladic, Echidnic	4L 2s, 6L 4s, 10L 6s, 10L 16s
3	5\36	166.66			6L 3s, 6L 9s, 15L 6s
4	2\36	66.66			4L 4s, 4L 8s, 4L 12s, 16L 4s
	4\36	133.33			4L 4s, 8L 4s, 8L 12s, 8L 20s
6	1\36	33.333
9	1\36	33.333	50/49, 49/48	Niner, Tritrizo	9L 9s
12	1\36	33.333	50/49, 49/48	Catler, Compton
18	1\36	33.333	50/49, 49/48

Scales

Main article: List of MOS scales in 36edo

Catler

• Lost spirit (approximated from Meantone in 31edo): 9 6 2 4 7 2 6

Hedgehog

• Hedgehog[14] MOS: 3 2 3 2 3 2 3 3 2 3 2 3 2 3
• Palace (subset of Hedgehog[14]): 5 5 5 6 5 5 5

833 Cent Golden Scale (Bohlen): 3 4 4 3 4 4 3

833 Cent Golden Scale MOS [11]: 3 1 3 3 1 3 1 3 3 1 3

Tuning by Ear

After 9edo and 19edo, 36edo is one of the easiest tuning systems to recreate tuning solely by ear, due to the way its purest intervals are arranged. If you view it as a lattice of 4 9edo's (which can be formed by stacking 9 7/6's with a comma of less than 2 cents) connected by 3/2's, you get a tonal diamond with a wolf note between the extreme corners of approximately 7.7 cents, about the same relative error as stacking 12 perfect 3/2's compared to 12edo and obviously a much smaller absolute error. It's a good system to use on large organs that have three manuals.

Tuning file: 9x4just

Instruments

36edo can be played on the Lumatone (see Lumatone mapping for 36edo) and using three instruments tuned to 12edo with different root notes.

Music

Ambient Esoterica

• A Trip to PRS with a Circle of Augmented 5ths (2024)

Miroslav Beinhauer

• Pieces For Sixth​-​Tone Harmonium (2024) Full album in 36edo

Ivan Bratt

• Boomers

E8 Heterotic

• "Elements - Lightning" from Elements (2020)

Francium

• Playing Children (2022) – for three pianos detuned by a sixth-tone from each other

Joe Hayseed

• Hay

Herman Klein

• Something (2022)

Claudi Meneghin

• Arietta with 5 Variations, for Organ (2024)

Joseph Monzo

• African Rhythms in 36-ET (2005)

NullPointerException Music

• Jungle Hillocks (2020)

Henri Pousseur

• Prospection (1952-1953) – for three pianos detuned by a sixth-tone from each other

Chris Vaisvil

• Thoughts in Legolas Tuning

Nick Vuci

• Fantasy for Sixth-Tone Harmonium (2022) – play

Stephen Weigel

• Exponentially More Lost and Forgetful (2017) played by flautists Orlando Cela and Wei Zhao