User:Tomruen/archive8
Wikipedia Day Meetup on January 18
[edit]
In the area? You are invited to the upcoming Minnesota meetup in commemoration of Wikipedia Day.
- Place: Seward Cafe
- 2129 E Franklin Ave, Minneapolis, MN 55404
- Date: Saturday, January 18, 2014
- Time: noon
- Place: Seward Cafe
For more info and to sign up (not required), see the meetup talk page.
This invitation was sent to users who were interested in past events. If you don't want to receive future invitations, you can remove your name from the invite list. —innotata 04:15, 10 January 2014 (UTC)
Long-standing mangled sentence in 4_21_polytope
[edit]The last sentence under the rectified 421 polytope section is mangled:
- The vertex figure is determined by removing the red node and node the neighbor nodea.
I traced it back to when it was merged from another article, and from that article all the way to its creation, and it appears to have been mangled from the beginning, so I have no way of knowing what the original intended meaning was. Could you fix this please? Thanks!—Tetracube (talk) 18:48, 30 January 2014 (UTC)
Image error
[edit]Your G(1,3) image https://en.wikipedia.org/wiki/File:Goldberg_polyhedron_3_1.png Has one miscoloured hexagon that should be green. (As well as a couple miscoloured pixels on the other side that should also be green). 204.191.92.201 (talk) 01:04, 21 February 2014 (UTC)
Subgroup graphs
[edit]Hi, I've made some SVG versions of your graphs at Talk:List of spherical symmetry groups#Subgroup relations. I also fixed two links which were incorrectly colored in your icosahedral .png, for consistency. ~ Keiji (iNVERTED) (Talk) 16:55, 2 March 2014 (UTC)

[[File:Grünbaumian great dodekicosahedron with triangles.png| Hi. I found some problems with those pictures in the article – the forms with added faces (e.g. cho+4{6/2}, giddy+20{6/2}, ri+12{10/4}, etc.) aren't shown properly, because the images don't have those added faces. I'd fix it myself, but Stella appears to be easily upset by faces such as {6/2} and {10/4}, and trying to "fake" them as {3} and {5/2} results in polyhedra with three faces to an edge which Stella is also quite upset by. So, could you please help? Thanks. Double sharp (talk) 08:00, 23 March 2014 (UTC)
- I also don't have any easy way to draw these correctly. Could some be marked up by hand? Tom Ruen (talk)
- Hmm...after playing around with what Stella will tolerate...will this do for cho+4{6/2}? It's not perfect, but I've got trouble seeing how to make it better. Double sharp (talk) 10:48, 24 March 2014 (UTC)
- (Doing this really makes me think I should get pictures ready for all these polyhedra with the absolutely correct colouring, but this might take a while.) Double sharp (talk) 10:50, 24 March 2014 (UTC)
- Hmm...after playing around with what Stella will tolerate...will this do for cho+4{6/2}? It's not perfect, but I've got trouble seeing how to make it better. Double sharp (talk) 10:48, 24 March 2014 (UTC)
(It appears to work properly sometimes, but not consistently. This is slightly irritating.) Double sharp (talk) 05:49, 30 March 2014 (UTC)
help with CDD diagrams?
[edit]Tidtidohi's diagram can't seem to be displayed probably with the already drawn elements: User:Double sharp/Polychora/Truncates (#32). Double sharp (talk) 14:09, 27 March 2014 (UTC)
- (and the more complicated diagrams on User:Double sharp/Polychora are a complete trainwreck currently because I've been faking the diagrams) Double sharp (talk) 14:31, 27 March 2014 (UTC)
- Hi DS, if you want to hand-draw what CDs you need, I can look to see what's the easiest way to implement my current system of top-middle-bottom rows. Some perhaps need to just be purely single-graphical in every markup case, like File:CDel K6 636 11.png. Tom Ruen (talk) 18:23, 28 March 2014 (UTC)
- All right, I'll go through them and show you the problematic ones... Double sharp (talk) 05:27, 29 March 2014 (UTC)
I think the problem is not so much that the diagrams are impossible to be displayed or anything like that using your system. The trouble is that not all the possible node markings are supported: e.g. there's no away I can create a branch with the top node marked 4/3 and the bottom node 4 (which BTW I need for #324, iquatoc). I think they should all work, except for the odd simplicial diagram (e.g. #553, kavahto, ((x4/3(x4o)3/2x4)), where each set of parentheses denotes a simplicial loop in the diagram (for example, (s3s3s5/2) is the small snub icosicosidodecahedron): thus the loops are (x4/3x4o), making a triangle, (x4o3/2x4) making another triangle sharing the "4" side with the first triangle, and the outermost loop encloses these triangles into a tetrahedron. Those few I think I need to make myself: I'm fine with that. But I think the current system ought to be extended with all possible rational node markings involving 3/2, 4/3, 5/2, 5/3, and 5/4. Double sharp (talk) 14:24, 3 April 2014 (UTC)
do Schwarz triangles have to be spherical?
[edit]Our article on Schwarz triangle defines them as spherical triangles: but then we then mention later on in the article that "The (2 3 7) Schwarz triangle is the smallest hyperbolic Schwarz triangle, and as such is of particular interest." So can we use the name for Euclidean and hyperbolic triangles as well? (Can we just call them triangular fundamental domains?) Double sharp (talk) 16:14, 29 March 2014 (UTC)
- I don't know. The article says its a generalization of Schwarz spherical triangle list. Tom Ruen (talk)
great icosahedron as faceting?
[edit]I was thinking, given the compound of two great icosahedra and retrosnub tetrahedron construction of the great icosahedron, that it should be possible to create an (irregular) great icosahedron by faceting a truncated octahedron. Is this true? (I've been trying in Stella: haven't got it yet.) Double sharp (talk) 03:21, 30 March 2014 (UTC)
- Sorry, faceting never fascinated me enough to worry about it. User:Steelpillow probably knows. Tom Ruen (talk) 03:36, 30 March 2014 (UTC)
- Thanks. I asked him at User talk:Steelpillow#great icosahedron as faceting?. Double sharp (talk) 04:59, 30 March 2014 (UTC)
Euclidean tilings
[edit]I collected some Wythoffian versions (for now just linear CD diagrams) at User:Double sharp/List of uniform tilings by Schwarz triangle. Star forms are given for only the Euclidean ones at the moment. Should I keep the hyperbolic tilings in here, given that they're already exhaustively documented in about the same way (Wythoff construction) on many other pages?
Pictures are a problem for the star forms, though, because of overlapping faces. (It's the same problem we get for spherical star polyhedra. There we have the option of flat-faced polyhedra: in Euclidean space we do not.) But they really should be there, just for consistency with the rest. (Maybe just colour one vertex, like I did at the picture on order-7 heptagrammic tiling?)
No plans to add the star hyperbolic tilings, BTW, as they're not well-documented at present. There are obviously an infinite number. (Some documented illustrative examples by McNeill: 3 | 7/2 3, 2 | 7/2 7, 3 | 7/3 7, 4 | 7/2 4, 4 | 5/2 4, 7/3 ∞ | 2.) Double sharp (talk) 05:42, 30 March 2014 (UTC)
- P.S. maybe for tetragonal fundamental domains on hyperbolic plane (2 3 4 5) is more representative, as it's the smallest with four different numbers. This is the one Klitzing uses as an illustration. Klitzing now has a page on these in 2D and 3D. Double sharp (talk) 05:46, 30 March 2014 (UTC)
Vertex configurations of sirsid and girsid
[edit]Four and a half years late, but I think I might have figured out what the problem is: see Talk:Great retrosnub icosidodecahedron. Double sharp (talk) 06:33, 30 March 2014 (UTC)
relationships among hyperoctahedral polytopes
[edit]Hi. Bowers has a diagram showing these on his page, but doesn't explain it: do you know what the relationship is? He gives the densities as well; each
(Coxeter-Dynkin diagram shorthand: space = 2. nothing = 3. , = 3/2. ' = 4. + = 4/2. '' = 4/3. ^ = 5. * = 5/2. *' = 5/3. ^' = 5/4. n = n. x = marked node, o = unmarked node. Parentheses loop the diagram. Proper CD diagrams later.)
1D: dyad
2D: square og oc
| Density | |
|---|---|
| 3 | 1 |
| square x'o | |
| og x''x |
oc x'x |
3D:
cube
gocco sirco
quith cotco tic
| Density | ||
|---|---|---|
| 7 | 3 | 1 |
| cube x'oo | ||
| gocco (o'x''x) |
sirco xo'x | |
| quith ox''x |
cotco (x'x''x) |
tic ox'x |
4D:
tes
gittith sidpith
wavitoth skiviphado srit
quitit thaquitoth thatoth tat
5D:
pent
ginnont scant
fawdint skatbacadint span
wavinant gikcavadint skivbadant sarn
quittin waquitant danbitot nottant tan
6D: (later)
Double sharp (talk) 14:42, 3 April 2014 (UTC)
- Sorry, stars are all mush in my brain, at least for quick thinking. Tom Ruen (talk) 01:12, 4 April 2014 (UTC)
Peak oil
[edit]You might be interested in [1]. Lot's of good analysis there. Cheers. — TimL • talk 23:11, 7 April 2014 (UTC)
- Thanks, I've read from is Gail Tverberg and the now retired The Oil Drum over many years. Tom Ruen (talk) 23:16, 7 April 2014 (UTC)
deleted
— Preceding unsigned comment added by Baumann Eduard (talk • contribs) 21:52, 8 April 2014 (UTC)
Error in picture?
[edit]I'm not sure that I have reached you. My wikipedia user page is "Baumann Eduard". Best regards Ed
I repeat my message: Dear Tomruen,
I’m talking about the following entry https://en.wikipedia.org/wiki/Conway_polyhedron_notation especially the illustration https://en.wikipedia.org/wiki/File:Conway_polyhedron_notation-examples2.png
Look at the part “gC”. I think that the red lines on top and on right side of the cube are wrong and should be the same as in part “dpC”. On top: the line left to right goes from front to back and should go from back to front. On the right side: the line bottom to top goes from back to front and should go from front to back.
Do you agree?
Kind regards Ed — Preceding unsigned comment added by Baumann Eduard (talk • contribs) 21:56, 8 April 2014 (UTC)
just wondering
[edit]would it be correct to call a runcitruncated tesseract a runcination of the tesseract? a truncation of the tesseract? because that's what the lede of runcinated tesseract seems to imply to me. (and why not runcinated tesseracts, since the article covers the runcination, runcicantellation, runcitruncation, and runcicantitruncation?) Double sharp (talk) 15:12, 9 April 2014 (UTC)
- Runcination means cutting faces, and truncation is cutting corners, so runcitruncation is both, and not either alone. Yes, this article probably should be plural, and then runcinated tesseract can direct to the first section. Tom Ruen (talk) 19:29, 9 April 2014 (UTC)
Eclipses visible from the US
[edit]I was thinking about creating an article for eclipses visible from the United States, but I see you already started one at User:SockPuppetForTomruen/List of solar eclipses visible from the United States. Can you move this to main article space, or would you mind if I did? I'd like to use it as a starting point. — TimL • talk 00:11, 10 April 2014 (UTC)
- Sure, do whatever you like, move or copy, looks like its only complete for 1950-2050. Tom Ruen (talk) 00:16, 10 April 2014 (UTC)
Nets of the 64 uniform polychora
[edit]I just realized that we don't seem to have pictures for all of them, so I'm uploading them. I'm using the Bowers name to avoid collisions with already present pictures: e.g. there was already File:Grand antiprism net.png so I used the Bowers File:Pentagonal double antiprismoid net.png. The 120-cell/600-cell family really does take a lot more time than the others to load in Stella... Double sharp (talk) 07:33, 12 April 2014 (UTC)
- Sounds good, although unsure why we need two Grand antiprism nets. Tom Ruen (talk) 07:41, 12 April 2014 (UTC)
- (We don't really, it's just that I made one as part of a set of 64 and I didn't want to waste it. Also this one is a square image, unlike yours.) Double sharp (talk) 07:45, 12 April 2014 (UTC)
- As for the Wythoffian nonuniform cases mentioned at Uniform polychoron, the easiest to do seems to be the runcic snub 24-cell (prissi, prismatorhombisnub icositetrachoron, s3s4o3x). (BTW it has a nonconvex isomorph, s3s4/3o3x.) The others aren't already present in the Stella library, so making them will be somewhat more of a challenge...but I'll think about how to do the snub tesseract and company. Do you have any ideas? :-) Double sharp (talk) 07:45, 12 April 2014 (UTC) Double sharp (talk) 07:45, 12 April 2014 (UTC)
P.S. Again for octahedral prism you already uploaded one, so I just used a slightly different name and put mine up so that I don't freak out later when I realize I haven't uploaded all 64. (Or 65, as it were, because I have a prissi net as well.) Double sharp (talk) 07:48, 12 April 2014 (UTC)
- I have no ambitions towards those, except as a few minor examples as given so far. Myself I'm content to work on the hyperbolic honeycomb vertex figure images that will take quite a while. I'm glad if you can add the nets to the uniform polychora articles. Tom Ruen (talk) 07:52, 12 April 2014 (UTC)
- Sure. So I will have all 64, plus 1 minor example. Double sharp (talk) 07:54, 12 April 2014 (UTC)
BTW if you're interested in another general family with only two uniform examples (like the duoantiprisms), Klitzing has this to say on the grand antiprism, which he identifies as the pentagonal member of a family of double antiprismoids:
"The general building rule for double antiprimoids would be: construct (in 4D) 2 perpendicular rings of 2n m-gonal antiprisms, respectively of 2m n-gonal antiprisms. Then connect the triangles of the one ring to the vertices of the other (and vice versa), and further more connect the lacing edges of the antiprism of one to the nearest similar edges of the other. Combinatorically all this filling stuff would be tets. But for general n,m the total figure cannot be made unit edged only. (Additionally, a single vertex orbit for sure is possible only when n=m.) Uniform exceptions occur for n=m=5 (gap) and n=m=5/3 (padiap)."
They're apparently also related to the duoantiprisms:
"Note that there is a crude mixture of gap and padiap too, which kind of is flattened somehow. In fact, gudap again uses a ring 10 paps and an orthogonal ring of 10 starps, but there the vertex set of both rings coincides. Accordingly the remaining space can be filled by 50 tets only." Double sharp (talk) 07:56, 12 April 2014 (UTC)

![]() Done All 65 done, will be inserted into articles later. Padiap projection uploaded with short article (like your gudap article) to follow. Might consider using sidtidap, ditdidap and gidtidap as further nonconvex Wythoffian antiprismatic examples – there are only 6, and they aren't just the same old Wythoffian constructions from star polychora or facetings of such polytopes that are not really notable. Double sharp (talk) 08:19, 12 April 2014 (UTC)
Done All 65 done, will be inserted into articles later. Padiap projection uploaded with short article (like your gudap article) to follow. Might consider using sidtidap, ditdidap and gidtidap as further nonconvex Wythoffian antiprismatic examples – there are only 6, and they aren't just the same old Wythoffian constructions from star polychora or facetings of such polytopes that are not really notable. Double sharp (talk) 08:19, 12 April 2014 (UTC)
- Symbols, if you wanted them: sidtidap = (oo*x) s =
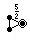
 , ditdidap = (o^x*o,) s =
, ditdidap = (o^x*o,) s = 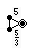
 , and gidtidap = (o,o^x) s =
, and gidtidap = (o,o^x) s = 
 Double sharp (talk) 14:32, 12 April 2014 (UTC)
Double sharp (talk) 14:32, 12 April 2014 (UTC)
- (Since there are only 4 known convex scaliforms, I uploaded the nets for them too. Possibly the duals of all of these could be done, because they are fair 4D dice – even the duals of the snub tesseract and similar nonuniform alternations.) Double sharp (talk) 14:32, 12 April 2014 (UTC)
Another nonuniform snub?
[edit]Did you try ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]()
![]()
![]() ? According to Klitzing it gives another scaliform polychoron (tutcup). Double sharp (talk) 13:15, 12 April 2014 (UTC)
? According to Klitzing it gives another scaliform polychoron (tutcup). Double sharp (talk) 13:15, 12 April 2014 (UTC)
- Looks fun: [2] - 2 truncated tetrahedrons, 6 tetrahedrons, 8 triangular cupola. It could be added this this table Uniform_polychoron#Octahedral_prisms:_BC3_.C3.97_A1. Okay, I'll add it. Tom Ruen (talk) 19:09, 12 April 2014 (UTC)
- p.s. I wonder about






 . Tom Ruen (talk) 20:59, 12 April 2014 (UTC)
. Tom Ruen (talk) 20:59, 12 April 2014 (UTC)
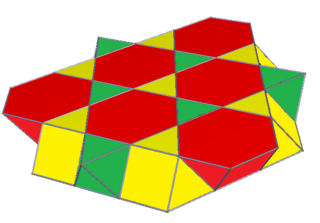 Up and down triangular cupola and octahedra A slice of a rectified cubic honeycomb |
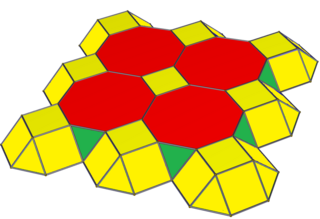 Up and down square cupola and tetrahedra. A slice of a Runcic cubic honeycomb |
- Still trying to get my head around these partial snubs – is the small rhombicuboctahedral prism the original polychoron that gets alternated to form tutcup? Double sharp (talk) 02:22, 13 April 2014 (UTC)
- I see two approaches. You can start with






 and do a confusing partial snub process, or start with
and do a confusing partial snub process, or start with 





 and move generator off the last mirror. I like the second approach better, example in reverse at Rhombicuboctahedron#Pyritohedral_symmetry. Tom Ruen (talk) 02:31, 13 April 2014 (UTC)
and move generator off the last mirror. I like the second approach better, example in reverse at Rhombicuboctahedron#Pyritohedral_symmetry. Tom Ruen (talk) 02:31, 13 April 2014 (UTC)
- OK, so in which article should it be covered? (Because you covered the runcic snub 24-cell with its original runcitruncated 24-cell.) Double sharp (talk) 02:42, 13 April 2014 (UTC)
- For now, I added to the nonuniform section of uniform polychoron, so I think that's all we can do, unless there's a citable source for scaliforms. Tom Ruen (talk) 02:47, 13 April 2014 (UTC)
- OK, added as a section to rhombicuboctahedral prism as a related polychoron (as an excuse to use my net picture). That covers all 64 nonduoprismatic uniform polytopes plus the two known Wythoffian convex scaliforms. (Are there Wythoff constructions for the other two, spidrox and bidex? I think not.) Double sharp (talk) 03:52, 13 April 2014 (UTC)
- For now, I added to the nonuniform section of uniform polychoron, so I think that's all we can do, unless there's a citable source for scaliforms. Tom Ruen (talk) 02:47, 13 April 2014 (UTC)
- OK, so in which article should it be covered? (Because you covered the runcic snub 24-cell with its original runcitruncated 24-cell.) Double sharp (talk) 02:42, 13 April 2014 (UTC)
- I see two approaches. You can start with
- Still trying to get my head around these partial snubs – is the small rhombicuboctahedral prism the original polychoron that gets alternated to form tutcup? Double sharp (talk) 02:22, 13 April 2014 (UTC)
- Ha, added another one,






 Tom Ruen (talk) 03:05, 13 April 2014 (UTC)
Tom Ruen (talk) 03:05, 13 April 2014 (UTC)
How about ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ? Do we have that one? Double sharp (talk) 05:06, 13 April 2014 (UTC)
? Do we have that one? Double sharp (talk) 05:06, 13 April 2014 (UTC)
- Gyrated_tetrahedral-octahedral_honeycomb#Construction_by_alternation
- Thanks! Double sharp (talk) 05:50, 13 April 2014 (UTC)
For tetracombs, since you have a page User:Tomruen/Convex uniform tetracomb, Klitzing has these partial nonuniform snubs: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Double sharp (talk) 11:56, 14 April 2014 (UTC)
. Double sharp (talk) 11:56, 14 April 2014 (UTC)
Playing around with some polychora
[edit]Apparently rectified sidtaxhi = wavhiddix and rectified dattady = swavixady. Rectified gidtaxhi is degenerate. Double sharp (talk) 04:28, 13 April 2014 (UTC)
Uniform polyhedra
[edit]Hey, I was thinking that we should show the partial snubs too for the uniform polyhedra. Currently the uniform polyhedron article only covers convex forms and AFAIK the only article that discusses Wythoffian constructions for all the forms is my list of uniform polyhedra by Schwarz triangle. As a result we only show the convex partial snubs, and I'm thinking that I could expand one of these articles with forms like ![]()
![]()
![]()
![]()
![]()
![]()
![]() (great icosahedron) – also the generalized "holosnub" where alternated odd polygons are treated as double-covered, so that {3} alternates to give {3}, {5} to {5/2}, creating forms like compound of two icosahedra = β3β3β, compound of two snub cubes = β3β4β, compound of two snub dodecahedra = β3β5β, etc. (The use of β instead of s here is just for emphasis and is unnecessary.) This incidentally leads to more duplicate constructions, e.g. o3o5β = small ditrigonal icosidodecahedron, β3β5o = small snub icosicosidodecahedron, β3o5x = small icosicosidodecahedron, β3o5x = small dodecicosidodecahedron. Double sharp (talk) 11:16, 14 April 2014 (UTC)
(great icosahedron) – also the generalized "holosnub" where alternated odd polygons are treated as double-covered, so that {3} alternates to give {3}, {5} to {5/2}, creating forms like compound of two icosahedra = β3β3β, compound of two snub cubes = β3β4β, compound of two snub dodecahedra = β3β5β, etc. (The use of β instead of s here is just for emphasis and is unnecessary.) This incidentally leads to more duplicate constructions, e.g. o3o5β = small ditrigonal icosidodecahedron, β3β5o = small snub icosicosidodecahedron, β3o5x = small icosicosidodecahedron, β3o5x = small dodecicosidodecahedron. Double sharp (talk) 11:16, 14 April 2014 (UTC)
Uniform tilings
[edit]I don't know if I asked before, but we're missing pictures for the Euclidean star-tilings, e.g. see User:Double sharp/List of uniform tilings by Schwarz triangle. Since colouring them traditionally results in a confusing messy blob of colours due to the overlapping geometry, what do you think I should do for these pictures? Double sharp (talk) 14:39, 14 April 2014 (UTC)
DYK for April 2014 lunar eclipse
[edit]| On 15 April 2014, Did you know was updated with a fact from the article April 2014 lunar eclipse, which you recently created or substantially expanded. The fact was ... that, according to the Blood Moon Prophecy, tonight's eclipse could be a sign that the end time is near? You are welcome to check how many page hits the article got while on the front page (here's how, live views, daily totals), and it may be added to the statistics page if the total is over 5,000. Finally, if you know of an interesting fact from another recently created article, then please feel free to suggest it on the Did you know talk page. |
slakr\ talk / 00:45, 15 April 2014 (UTC)
Moon photo
[edit]Would the image have come out better if you used a higher ISO and a shorter exposure time? Considering how fast the eclipse was occurring, isn't three seconds too long? 166.137.176.19 (talk) 05:52, 16 April 2014 (UTC)
- The 3-second exposure was with a telescope with a computer motor drive that followed the earth's motion. Tom Ruen (talk) 06:29, 16 April 2014 (UTC)
Uniform polychora labellings
[edit]In 3D we have the Wythoff symbol and vertex configuration to supplement the CD diagrams. Do such things exist in 4D, or do I just have to do what I did at User:Double sharp/List of uniform polychora by Goursat tetrahedron to label the individual columns?
P.S. using these becomes somewhat problematic once we move past linear diagrams. Double sharp (talk) 14:35, 16 April 2014 (UTC)
- There are vertex figures only, Coxeter diagrams replace Wythoff symbols in general. Tom Ruen (talk) 19:23, 16 April 2014 (UTC)
cupolae
[edit]think we have enough examples in the template? Stella stops here at heptagonal: McNeill goes up to decagonal. (And me being a uniform-polytope enthusiast, they're most interesting at n = 3, 4, and 5!) Double sharp (talk) 07:31, 18 April 2014 (UTC)
- also I think that if we are going to mention the nonconvex isomorphs at all for the Johnsons they should be just sections in the analogous convex forms. Double sharp (talk) 07:33, 18 April 2014 (UTC)
Actually I think the cases n = 4/3, 5/2, 5/3, 5/4 might make sense to include because they are closely related to uniform polyhedra (querco, qrid, their facetings, and the ditrigonaries). So I started an article on the crossed square cupola.
(Excavation is hard to visualize. How did I do? Do you have any ideas to improve it?) Double sharp (talk) 13:48, 18 April 2014 (UTC)
- What you did looks good. I'd consider putting the crossed forms INTO the convex article, like square cupola#crossed square cupola. 23:04, 18 April 2014 (UTC)
- Well, for {4/3} it was starting to get a bit big... Double sharp (talk) 23:51, 18 April 2014 (UTC)
I'm obviously starting to be too focused on their topological structure! (Q 4 = Q 4/3 and Q 5 = Q 5/3 topologically, but geometrically they are not. Nevertheless they are all part of the cupolae family, so to be consistent maybe the cupola template should now say convex cupolae?!)
For Q 5/3, I didn't give the pictures for the 12 gyrate quasirhombicosidodecahedra simply because I have no idea how to make them in Stella. Nevertheless McNeill's site gives VRML models for all 12 (plus the base quasirhombicosidodecahedron). Double sharp (talk) 08:06, 19 April 2014 (UTC)
To give a reasonable overview on these isomorphs (the augmented quasitruncated hexahedron and similar things can be covered in the article of the base uniform polyhedron), we also probably need great pentagonal rotunda, which is half of a great icosidodecahedron, but I have no idea how to make one in Stella. Double sharp (talk) 08:06, 19 April 2014 (UTC)
- It's your call to sort them out. You can see I'm more interested in forms that are topologically identical to a convex form (which should be in a shared article ), or vertex arrangement sharing, also seems good to put in the same article as a convex form. But I've not thought enough to see what all these forms are in detail. Tom Ruen (talk) 08:20, 19 April 2014 (UTC)
- Mostly agreed about the shared articles, but since the {5/2}- and {5/4}-cuploids don't have topologically identical convex forms, I just gave all the square and pentagonal cupolae their own articles. The rest would go into the articles of the base Johnson solids, with the obstacle that I have absolutely no idea how to make most of them in Stella. So I guess those will have to wait until I sort out the pictures. Double sharp (talk) 08:27, 19 April 2014 (UTC)
...Talk:Crossed pentagrammic cupola has a table ready for images of the 12 isomorphs for J72-J83. (I suspect the images aren't really helping visualization, but at least now there are pictures!) I could make most of the other Johnson isomorphs as well, except those for the sporadics. Double sharp (talk) 15:13, 19 April 2014 (UTC)
Order of discovery of the uniform polyhedra
[edit]Hi, I just found this old subpage of mine and thought you might be interested: User:Double sharp/Uniform polyhedra discovery. Double sharp (talk) 08:14, 19 April 2014 (UTC)
- Do you want to link all the discoverer's into individual articles? Tom Ruen (talk) 08:36, 19 April 2014 (UTC)
- Sure! Double sharp (talk) 09:59, 19 April 2014 (UTC)
Incidentally I'm thinking that to avoid all the qualifiers like nonconvex great rhombicosidodecahedron (the "nonconvex" isn't really part of the name, but I have to include it all the time to distinguish it from the truncated icosidodecahedron), we could switch to using the Wenninger names for the uniform polyhedra, which would just use the following substitutions:
- W13: Rhombicuboctahedron → Small rhombicuboctahedron (I guess we don't have to do this: it's unnecessary, not very agreed on, and inconsistent with the ones below like W93)
- W14: Rhombicosidodecahedron → Small rhombicosidodecahedron (see W13)
- W15: Truncated cuboctahedron, 'rhombitruncated cuboctahedron → Great rhombicuboctahedron (see W13)
- W16: Truncated icosidodecahedron, rhombitruncated icosidodecahedron → Great rhombicosidodecahedron (see W13)
- (W17: Snub cube → Snub cuboctahedron? Not Wenninger, but attested and more logical given the other snubs)
- (W18: Snub dodecahedron → Snub icosidodecahedron? See W17)
- W79: Cubitruncated cuboctahedron → Cuboctatruncated cuboctahedron
- W84: Icositruncated dodecadodecahedron → Icosidodecatruncated icosidodecahedron
- W85: (Nonconvex) great rhombicuboctahedron → Quasirhombicuboctahedron
- W92: Stellated truncated hexahedron → Quasitruncated hexahedron
- W93: Great truncated cuboctahedron → Quasitruncated cuboctahedron
- W97: Small stellated truncated dodecahedron → Quasitruncated small stellated dodecahedron
- W98: Truncated dodecadodecahedron → Quasitruncated dodecadodecahedron
- W104: Great stellated truncated dodecahedron → Quasitruncated great stellated dodecahedron
- W105: (Nonconvex) great rhombicosidodecahedron → Quasirhombicosidodecahedron
- W108: Great truncated icosidodecahedron → Great quasitruncated icosidodecahedron
My proposal would change these all except W13 to W16. That would maximize consistency in naming and avoid all the ambiguities. Also, it would be more correct: the stellated truncated hexahedron is not a stellation of the truncated cube, but it is a quasitruncation of the cube. (Lastly, it's not OR, and yet coincides with Bowers naming, which I like a lot! Although I would prefer it if he would at least call the quasitruncated cuboctahedron a great quasirhombicuboctahedron, etc., to be consistent. So I chose the truncated rectified names because they're all attested reliably.) Double sharp (talk) 14:27, 19 April 2014 (UTC)
- Documenting alternate names to verified sources is great, but renaming the articles is a trickier. Wenninger got the names from Johnson, but the article names used now are largely copied from MathWorld, and those come from Johnson's newer names, so that means alternate names need to be documented by date as well as person. Anyway, none of the newer names include the prefix quasi[3]. Lastly, Johnson would agree with Snub cuboctahedron, but Kepler wins for historical reasons, even if somewhat ambiguous, so there's an implicit rectification, i.e. sr{4,3}, sr{5,3}, but it is harmless since s{4,3},s{5,3} can't exist as rectified snubs. Tom Ruen (talk) 20:46, 19 April 2014 (UTC)
- TBH outside George Hart's and Jim McNeill's websites I've never actually seen Johnson's newer names. According to MathWorld, they're in his (forthcoming since 1996) book Uniform Polytopes.
- As for the naming, Mathworld says Wenninger was the first published source to include names: if this is true (I don't really trust MathWorld all that much) then it would make a lot of sense to follow him throughout, with the quasi- names! (They are quite correct, since quasitruncate means retrograde truncate, quasirhombate means retrograde cantellate, etc. Johnson would use stellatruncate for the first and great rhombi- for the second, which isn't really consistent since they're both isomorphic to the original convex polyhedra.) Double sharp (talk) 02:49, 20 April 2014 (UTC)
- The oldest "new" listing is from construction in 1993 [4], which are taken from (Wenninger 1984, Dual models), so looks like 1984 names should stand if any. I verified them as BOLD above, including Snub cuboctahedron, but also for others, he abandoned rhombitruncated for Kepler's names later. Tom Ruen (talk) 04:00, 20 April 2014 (UTC)
- The polyhedron names listed in tables 5 to 8 are taken from [W2], where they are attributed to Norman W. Johnson, but note they sometimes vary among authors.
Noncompact hyperbolic honeycombs
[edit]Is the "prism" of a hyperbolic plane tessellation (e.g. heptagonal tiling prism, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ) always a noncompact hyperbolic honeycomb? Double sharp (talk) 12:36, 24 April 2014 (UTC)
) always a noncompact hyperbolic honeycomb? Double sharp (talk) 12:36, 24 April 2014 (UTC)
Uniform dual faces
[edit]
You can remove this notice at any time by removing the {{Talkback}} or {{Tb}} template.
Double sharp (talk) 12:33, 27 April 2014 (UTC)
- Replied again. Double sharp (talk) 12:44, 27 April 2014 (UTC)
- ...and again. Double sharp (talk) 12:49, 27 April 2014 (UTC)
- I have a watch on your user talk page, so this isn't needed. Tom Ruen (talk) 12:58, 27 April 2014 (UTC)
- OK, I won't leave this in future. Double sharp (talk) 13:12, 27 April 2014 (UTC)
Face images done for DU1 to DU40 Double sharp (talk) 14:06, 28 April 2014 (UTC)
- Done all! I used the black background because the white lines wouldn't show up readily otherwise (I dunno why but they still appear white even if I set the background to white?!).
- Stella automatically colours in only the externally visible parts of the face in orange. Double sharp (talk) 14:21, 28 April 2014 (UTC)
- You could invert the colors? Tom Ruen (talk) 14:31, 28 April 2014 (UTC)
- Yes but didn't have the patience to at the moment. I could go through them again when I don't feel quite as impatient about it (maybe in a day or two?) Double sharp (talk) 14:38, 28 April 2014 (UTC)
- I linked the face images up to the convex Catalan solids, and I'll leave the dual uniform star to you. Tom Ruen (talk) 23:16, 30 April 2014 (UTC)
- Since the duals of the uniform polychora are isochoric, maybe we should also create pictures of their cells. (For the convex ones only, naturally.) Double sharp (talk) 03:56, 1 May 2014 (UTC)
- I'm open on the dual uniform polychora cell images but dislike projective ambiguity, same reason I prefer symbolic vertex figure diagrams where the topology is what's important, but I don't know what's important for the dual cells besides general shape, although at least we now have names for all the tetrahedral symmetries, but not for all the irregular pyramids, etc. Tom Ruen (talk) 04:44, 1 May 2014 (UTC)
- p.s. Robert Webb is starting a Stella update, and will include Coxeter notation symmetry, AND maybe will take my advice and group the Convex uniform polychora separate from all the stars! Tom Ruen (talk) 04:45, 1 May 2014 (UTC)
- They are already separated in Stella 4.4: there's a section called "Convex" in the 4D Library that only gives you the 64 nonduoprismatic convex uniform polychora. Of course all of these are duplicated in the main listing, which also includes the stars.
- Projective ambiguity is not an issue if you also label the edges with numbers (like
 ,
,  . These are front and back views of the vertex figure of the great duoantiprism.). Double sharp (talk) 05:24, 1 May 2014 (UTC)
. These are front and back views of the vertex figure of the great duoantiprism.). Double sharp (talk) 05:24, 1 May 2014 (UTC)
- p.s. Robert Webb is starting a Stella update, and will include Coxeter notation symmetry, AND maybe will take my advice and group the Convex uniform polychora separate from all the stars! Tom Ruen (talk) 04:45, 1 May 2014 (UTC)
I inverted the colours of all 65 images. (65 = 75 minus the 10 with infinite duals.) Double sharp (talk) 12:43, 2 May 2014 (UTC)
- Very good - I saw on the Catalan solid page. Looks great. Tom Ruen (talk) 22:11, 2 May 2014 (UTC)
those old polytopic WikiProjects
[edit]Am thinking that we probably could merge Wikipedia:WikiProject Polyhedra and Wikipedia:WikiProject Uniform Polytopes into a more general Wikipedia:WikiProject Polytopes. (No uniform, to acommodate the notable 3D cases like Johnson solids, uniform duals, etc.) That would cover pretty much everything I can think of for this area. Double sharp (talk) 11:27, 1 May 2014 (UTC)
- I'm content to keep them separate, given 3D models are more accessible than general polytopes. But who knows if anyone wants to use them? Tom Ruen (talk) 20:06, 1 May 2014 (UTC)
since you've been around for the requisite duration and made the requisite number of edits
[edit]I gave you a service award. Double sharp (talk) 01:48, 3 May 2014 (UTC)
[[File:Editor - orichalcum star.jpg|frame|left|
]]
Pentakis snub dodecahedron; good job!
[edit]I love the image you made of a pentakis snub dodecahedron. Any chance of making one for a triakis snub disphenoid, or maybe even a triakis version of one of the four other irregular deltahedra? Robo37 (talk) 11:52, 27 May 2014 (UTC)
- Maybe, I'm not sure what they are for. Is the center point coplanar with the original triangle, or positioned above it by some factor, and how would you decide what height above the face? Tom Ruen (talk) 17:53, 27 May 2014 (UTC)
- I was just thinking that deltahedrons would are the most logical choice after the platonic solids, having each face regular and in the same shape. It wouldn't be coplanar, instead I like to visualize the shapes as having a triangular based pyramid/tetrahedron on each side, similar to how the triakis platonic solids are shown on the Kleetope page. Robo37 (talk) 21:23, 27 May 2014 (UTC)
- The Catalan solids at Kleetope are based as duals to the Archimedean solids. So I don't know what relation determines the altitude of the pyramids in general. If the polyhedron points existed on a sphere, that would determine the heights of the new points, but that's not how even the symmetric the Catalan solids are defined. Tom Ruen (talk) 21:32, 27 May 2014 (UTC)
- For Kleetopes, one has to make an arbitrary choice: they're defined by their combinatorial structure, not by their exact geometry. —David Eppstein (talk) 06:04, 4 July 2014 (UTC)
Invitation to join the Ten Year Society
[edit]
Dear Tom,
I'd like to extend a cordial invitation to you to join the Ten Year Society, an informal group for editors who've been participating in the Wikipedia project for ten years or more.
Best regards, — Scott • talk 13:04, 2 June 2014 (UTC)
Dual tilings
[edit]I see you have decided against having separate articles on several well-known and quite independently notable tilings such as the Cairo pentagonal tiling, Tetrakis square tiling, and Rhombille tiling that I have worked hard to find *specific* and reliable sources for, and are merging them to the badly-sourced articles on their dual tilings. I don't think this is a good idea. What makes regular polygons special that their tilings should have articles and tilings with other shapes should not? But does this mean we will also not have separate articles on all the many (not so notable and also badly sourced) truncated/bitruncated/runcinated/kis/snub polytopes and will merge them all to their non-truncated versions? That might be an improvement. —David Eppstein (talk) 06:02, 4 July 2014 (UTC)
- Hi David. Yes, perhaps I'm overstepping, but with uniform duals it seemed most having minimum special information, but also with higher dimensional unform polytopes/honeycombs. ... I see the template tables have name from articles, {{PAGENAME}}, need to fix that! Tom Ruen (talk) 06:11, 4 July 2014 (UTC)
- They are independently notable and deserve their own articles. Notability of the subjects is much more important than uniformity of the article naming structure. This goes not only for these tilings but also for the bitruncated kis-snub things, which are mostly NOT independently notable. —David Eppstein (talk) 06:14, 4 July 2014 (UTC)
- Okay, sure, I see you revert them. Tom Ruen (talk) 06:16, 4 July 2014 (UTC)
polygon orthogonal hypercube basic vector scalar
[edit]I had requested basis vector scalar generation methodology via Rocchini's user page.
You had answered, by providing a solution of base vectors scalars per orthogonalized hypercube for 3 < n < 11 dimensions ( tesseract to dekeract ), I thank you.
Is there a simple formulae, which you could perhaps reveal here?
I would also like to generate z vector values for 3 < n < 11 dimensions, since I plan to generate any one of these midst a tri dimensional engine.
I had previously patched Rocchini's 120 cell polygon c++ code, and got them all running. However upon executing the code resource you provided,
I found it uncompilable.
I would like to incur knowledge regarding basis vector generation. Can you provide me with a condensed formulation? — Preceding unsigned comment added by 69.160.117.21 (talk) 08:57, 10 July 2014 (UTC)
edit 0: I realize all this may indeed be related to Caley Graphs of {0,1}d... Can this be condensed into a simpler formulation? — Preceding unsigned comment added by JordanMicahBennett (talk • contribs) 09:10, 10 July 2014 (UTC)
edit 1: I have been analyzing Rocchini's code, more specifically, the "compute_coxeter_plane" routine. (midst kalei.cpp) It is quite complex. From this I detect that thus far, there aren't really any quick ways of achieving our base vector direction scalars.
edit final: I realize that naturally, I could easily assign arbitrary depth vector component, therein no coxeter dynkin z values are required. — Preceding unsigned comment added by JordanMicahBennett (talk • contribs) 12:37, 10 July 2014 (UTC)
- Hi Jordan, I think User:Jgmoxness's reply at User_talk:Rocchini is as good as anything I can describe. Tom Ruen (talk) 20:19, 10 July 2014 (UTC)
- Here's an example of my solution for the hypercubes, so the blue edges show ONE Petrie polygon (among 4 possible in the cube), and their mapping into a regular hexagon. So you have to solve for the A matrix elements that do the mapping. And I think my vectors are (A11,A21,A21), and (A12,A22,A32) in the graphic. Tom Ruen (talk) 23:21, 10 July 2014 (UTC)
- view1=(0.408248290464,0.816496580928,0.408248290464)
- view2=(-0.707106781187,0.000000000000,0.707106781187)

I thank you. I hadn't yet seen User:Jgmoxness' response. He has provided me with the aim I sought. You have also clarified my view on things. — Preceding unsigned comment added by JordanMicahBennett (talk • contribs) 09:04, 12 July 2014 (UTC)
Good day tom.
Though I had long understood, that indeed, magic values via Claudio Rochhini's 600-cell manifest as some form of projection vector scalars, I still have issues with actually producting this [u,v] set for any orthogonalized hypercube.
I had of recent re-visited User:jgmoxness's page, and I realize that he himself experienced some difficulties in processing the purpose of the basis vectors:
Here is a response to him via yourself:
I don't know if I can explain any better by email. My main trick is given a sequence of vertices of a regular polytope, to project as a regular m-gonal Petrie polygon. So that sets up a system of equations as dot products: [dot(u,p(i),dot(v,p(i)]=[cos(2*pi*i/m),sin(2*pi*i/m)]. I solve for u,v vectors. I used that for the simplex and hypercube families. So the weakness of the trick is knowing the petrie polygon sequence. That's easy for a simplex since all vertices are used, so any order is a petrie polygon. A hypercube was easy, just a zig-zag path from one vertex n-steps towards its opposite. (For other basis, like Ak, sometimes I'd isolate regular k-simplex face of other polytopes, and then compute a uv Coxeter plane basis in that subspace, and map that uv basis back to the full space.
I also recall you've given me a set of solution basis vectors, however, I would like to generate them myself, for the purpose of an artificial intelligence routine I am writing.
For example, for a penteract polygon, what do I use or need so as to generate such basis vectors?
Thank you kindly. — Preceding unsigned comment added by JordanMicahBennett (talk • contribs) 08:05, 14 July 2014 (UTC)
Nomination for deletion of Template:Stella4D
[edit]![]() Template:Stella4D has been nominated for deletion. You are invited to comment on the discussion at the template's entry on the Templates for discussion page. Magioladitis (talk) 12:07, 24 August 2014 (UTC)
Template:Stella4D has been nominated for deletion. You are invited to comment on the discussion at the template's entry on the Templates for discussion page. Magioladitis (talk) 12:07, 24 August 2014 (UTC)
Runcinated 5-cube verf
[edit]I'm wondering if there's an error in the figure for the vertex figure of the runcinated 5-cube, File:Runcinated_penteract_verf.png, and the similar vertex figure of the runcinated 5-crosspolytope, File:Runcinated_pentacross_verf.png. Of the six outer vertices, five are incident to 5 edges, while the sixth is incident to 6 edges, which seems to defy the expected level of symmetry. Is it correct? I'm trying to figure out the number of flags in these figures.
Thanks. --kundor (talk) 14:24, 26 August 2014 (UTC)
- Also, the given vertex figure File:Stericantellated_5-simplex_verf.png and File:Stericantellated_5-orthoplex_verf.png seem to have vertices incident to only 3 edges, which isn't possible for a 4-polytope. I'm not sure how to interpret these figures. --kundor (talk) 18:57, 26 August 2014 (UTC)
You can see the full list here, with general labels for all the linear forms, so runcinated {p,q,r,s} has the same verf structure for any {p,q,r,s} values. They can be confusing since they are hand-drawn, and not necessarily close to any realistic perspective or projective arrangement. Ideally you should be able to extract all the 4-faces, cells, faces, and edges from the verf cells, faces, edges, and vertices. I can look more closely again and see if I can spot any errors. Tom Ruen (talk) 19:14, 26 August 2014 (UTC)
- Yes, all the vertex figures for runcinated {p,q,r,s} have the top-right vertex incident to three yellow edges, while all the other outer vertices are only incident to two yellow edges. I think this may be an error. (In particular, calculating the number of flags of the runcinated 5-cube or 5-simplex matches the pattern I'm expecting if I omit that extra yellow edge, and the various faces it implies.) --kundor (talk) 01:37, 5 September 2014 (UTC)
- Got it. Thanks for your persistence. There was a stray yellow edge on the upper left. I uploaded corrections. Tom Ruen (talk) 02:16, 5 September 2014 (UTC)
- Cool, thanks! I'm still wondering what's up in the stericantellated figures. Here's a picture where I've indicated the vertex I'm confused about with an arrow. It seems to only have three incident edges. https://i.imgur.com/7kRKX7jl.png?1 --kundor (talk) 00:34, 6 September 2014 (UTC)
Template:Uniform dual polyhedron stat table
[edit]Hi Tomruen, I just wanted to make sure you were aware that your edit to Template:Uniform dual polyhedron stat table caused a load of missing images to be flagged on Category:Articles with missing files.
- File:DU03_facets.png on Octahemioctahedron
- File:DU04_facets.png on Tetrahemihexahedron
- File:DU15_facets.png on Cubohemioctahedron
- File:DU49_facets.png on Small icosihemidodecacron
- File:DU51_facets.png on Small dodecahemidodecacron
- File:DU62_facets.png on Small dodecahemicosacron
- File:DU65_facets.png on Great dodecahemicosahedron
- File:DU70_facets.png on Great dodecahemidodecacron
- File:DU71_facets.png on Great icosihemidodecacron
- File:DU75_facets.png on Great dirhombicosidodecacron
Cheers KylieTastic (talk) 12:47, 30 August 2014 (UTC)
- I think there's a way to suppress them, but I don't know how. Otherwise I could upload images that says "None" or something silly. Tom Ruen (talk) 23:22, 30 August 2014 (UTC)
- Hi, if they aren't meant to exist I'll have a look at the template and add a way to remove if it does not have one already, I just wanted to make sure it wasn't an oversight or you were planning to make them. Cheers KylieTastic (talk) 12:21, 31 August 2014 (UTC)
- Thanks! The template is simple, but I tried to be tricky with systemic filenames, but some don't exist, shouldn't exist, as you found. 173.240.25.249 (talk) 12:23, 31 August 2014 (UTC)
- Should all be fixed up now. I see you noticed anyway due to the 'Thank' on the template. I had to alter Template:Uniform polyhedra db as well just to pass the parameter through. I've looked through a random selection of both templates usages to double check I didn't break anything, so all look fine to me. Let me know if you spot any issues. Cheers KylieTastic (talk) 14:28, 31 August 2014 (UTC)
- Thanks again, looks great! Tom Ruen (talk) 08:23, 1 September 2014 (UTC)
Proposed deletion 11-cube
[edit]I've proposed deletion of 11-cube as a hoax pushing the name Jennoid but redirecting it would be fine too. Dmcq (talk) 18:55, 8 September 2014 (UTC)
Tiling picture
[edit]You've posted so many great pictures that I hate to complain about one, but this one - File:Uniform_tiling_44-t12.png - is slightly slanted (look near the bottom), and I find that disconcerting. It may also create some funny effects on what are supposed to be straight lines. John Baez (talk) 17:52, 20 September 2014 (UTC)
- Hi John, yes, troublesome, created from free software, but no control over orientation. [5] I can rotate by hand, but will still be aliasing. I rotated the full set of square tilings. Tom Ruen (talk) 04:06, 21 September 2014 (UTC)

|

|

|

|

|

|

|
October 2014 lunar eclipse
[edit]hi...
was curious to know why you removed my descriptions of what to see during a lunar eclipse. the article was just a stub and needed more content. I intend to put those back but wanted to know your reasoning first. thanks.
clear skies, NightSkyGuy — Preceding unsigned comment added by NightSkyGuy (talk • contribs) 16:38, 27 September 2014 (UTC)
- There was similar generic content at lunar eclipse, so I copied it into Template:Total lunar eclipse contacts and shared it to the current eclipse, with the contact points labeled. Feel free to expand the content there, assuming it is also generic to all eclipses. Tom Ruen (talk) 17:12, 27 September 2014 (UTC)
Lunar Eclipse Class Project
[edit]Thanks for the feedback! Do you have any advice for us with regard to potential topics for edits? We're also making our first edits tonight (1504 lunar eclipse and lunar vs. solar eclipse, please let us know what you think!
KieranKinnare (talk) 01:08, 2 October 2014 (UTC)
Honeycomb with tetrahedra and truncated tetrahedra
[edit]I'm guessing if someone here knows this, it's you: There is a 3d honeycomb made from tetrahedra and truncated tetrahedra, closely resembling the Triakis truncated tetrahedral honeycomb (but with tetrahedra instead of the triakis parts). Does it have a name? Do we have an article on it? —David Eppstein (talk) 07:23, 7 October 2014 (UTC)
- quarter cubic honeycomb Tom Ruen (talk) 08:44, 7 October 2014 (UTC)
- Thanks, exactly the one I was looking for. —David Eppstein (talk) 22:30, 16 October 2014 (UTC)
Sorry, I was making a big change and while editing, you made some changes too. I overwrote your changes. Bgwhite (talk) 23:35, 21 October 2014 (UTC)
Eclipse photo
[edit]I like your photo of the eclipse today. Did you put your camera on a telescope? Bubba73 You talkin' to me? 04:07, 24 October 2014 (UTC)
- Thanks! I just used my megazoom camera, Canon PowerShot SX50 HS, a tripid, and with neutral filters, (×1/40000).
- Thanks. I was planning to take photos of the eclipse. I have a DX format DSLR, and was using a 300mm lens (the longest one I have). I made test shots yesterday, and they aren't nearly as good as yours, e.g. the sunspots. But about 20 minutes before the eclipse started, I wasn't watching where I was stepping, had a bad fall, and had to go to urgent care. Bubba73 You talkin' to me? 04:19, 24 October 2014 (UTC)
Thought you might like this
[edit]I saw your edits about pararotations and I thought you might be interested in this video showing what its like to live in hyperbolic space: https://www.youtube.com/watch?v=AGLPbSMxSUM
A pararotation is a parabolic transformation; in the disk model of hyperbolic space, parabolic transformations do rotate everything around a point at infinity. I tried to find a video of it, but I can't.
The 'mirrors' in the article you quoted are planes of reflection or lines of reflection. If you reflect the hyperbolic plane about two lines intersecting at a single point, you get a parabolic transformation.
I really like your edits! Brirush (talk) 02:59, 12 November 2014 (UTC)
- Also, this website, although I'm sure you've seen it: https://geometrygames.org Brirush (talk) 03:21, 12 November 2014 (UTC)
Thanks! Yes, I seen both, and many polyhedra and tiling images I've uploaded to Wikipedia were made by KaleidoTile.
I actually still had some mental confusion over pararotations versus translations, but made these images to clarify. The lines are reflection lines (mirrors) and fundamental domains are alternately colored areas. pararotation and translations arise from the sequence of two reflections. Tom Ruen (talk) 03:31, 12 November 2014 (UTC)
| Striation or pararotation | Translation |
|---|---|
 |
 |
Your translation picture is of a hyperbolic (or loxodromic) element. You can see the attracting point and repelling point. Also, the mirrors are completely disjoint, which is another characterization of hyperbolic elements. The one on the left is indeed a parabolic/pararotation. By the way, are these pictures public? I might use them in a talk at some point, if that's all right. Brirush (talk) 03:49, 12 November 2014 (UTC)
- Yes, they are public, hand-filter with MSPaint from images at 642 symmetry and iii symmetry tables. It would be better to compute them directly. A nicer SVG image is here File:Horocycle_normals.svg, but it didn't have equal-distance lines like I wanted. Tom Ruen (talk) 03:56, 12 November 2014 (UTC)
By the way, I just realized one source of confusion:a parabolic is a pararotation in the disk model, but it in the upper half-plane model, a parabolic element can take the form z->z+1, which is the same form as a Euclidean translation. Anyways, sorry for posting again. Brirush (talk) 04:33, 12 November 2014 (UTC)
Template:Uniform polyteron stat table
[edit]hi, I fixed Template:Uniform polyteron stat table. note that the colour of the top header has changed because before it was ignoring the bgcolor parameter, but now it's not. Frietjes (talk) 00:40, 19 November 2014 (UTC)
How to draw a polyhedron
[edit] I want to know how did you draw a goldberg polyhedron. Could you tell me the concrete way? --Eric4266 (talk) 07:47, 10 December 2014 (UTC)
I want to know how did you draw a goldberg polyhedron. Could you tell me the concrete way? --Eric4266 (talk) 07:47, 10 December 2014 (UTC)
- I'm sorry. Many I copied from elsewhere, this one recolored from File:Géodes V duales.PNG. Tom Ruen (talk) 07:50, 10 December 2014 (UTC)
Octahedron
[edit]I am asking for your view about this as you are a major contributor to the octahedron article.
The section Octahedron#Orthogonal projections shows a special orthogonal projection described as "normal to a face". It is certainly special, and orthogonal, but I can't see how it is normal to a face. Is this an error, or have I misunderstood something? Maproom (talk) 10:46, 18 December 2014 (UTC)
- Let's improve the wording. Its like the the "Edge" view, but rotated 90 degrees on a horizontal axis. Tom Ruen (talk) 11:12, 18 December 2014 (UTC)
Non-convex uniform polychora and the UPP
[edit]Hi Tom, You might want to take a look at the discussion at Talk:4-polytope#Unknown_total_number_of_nonconvex_uniform_4-polytopes. — Cheers, Steelpillow (Talk) 11:04, 19 December 2014 (UTC)
Nomination for merging of Template:Infobox Solar eclipse2
[edit]![]() Template:Infobox Solar eclipse2 has been nominated for merging with Template:Infobox Solar eclipse. You are invited to comment on the discussion at the template's entry on the Templates for discussion page. Thank you. Andy Mabbett (Pigsonthewing); Talk to Andy; Andy's edits 16:13, 21 December 2014 (UTC)
Template:Infobox Solar eclipse2 has been nominated for merging with Template:Infobox Solar eclipse. You are invited to comment on the discussion at the template's entry on the Templates for discussion page. Thank you. Andy Mabbett (Pigsonthewing); Talk to Andy; Andy's edits 16:13, 21 December 2014 (UTC)



