Continuous Bernoulli distribution
|
Probability density function 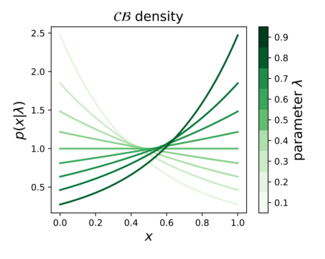 | |||
| Notation | |||
|---|---|---|---|
| Parameters | |||
| Support | |||
|
where | |||
| CDF | |||
| Mean | |||
| Variance | |||
In probability theory, statistics, and machine learning, the continuous Bernoulli distribution[1][2][3] is a family of continuous probability distributions parameterized by a single shape parameter , defined on the unit interval , by:
The continuous Bernoulli distribution arises in deep learning and computer vision, specifically in the context of variational autoencoders,[4][5] for modeling the pixel intensities of natural images. As such, it defines a proper probabilistic counterpart for the commonly used binary cross entropy loss, which is often applied to continuous, -valued data.[6][7][8][9] This practice amounts to ignoring the normalizing constant of the continuous Bernoulli distribution, since the binary cross entropy loss only defines a true log-likelihood for discrete, -valued data.
The continuous Bernoulli also defines an exponential family of distributions. Writing for the natural parameter, the density can be rewritten in canonical form: .
Statistical inference
[edit]Given a sample of points with , the maximum likelihood estimator of is the empirical mean,
Equivalently, the estimator for the natural parameter is the logit of ,
Related distributions
[edit]Bernoulli distribution
[edit]The continuous Bernoulli can be thought of as a continuous relaxation of the Bernoulli distribution, which is defined on the discrete set by the probability mass function:
where is a scalar parameter between 0 and 1. Applying this same functional form on the continuous interval results in the continuous Bernoulli probability density function, up to a normalizing constant.
Beta distribution
[edit]The Beta distribution has the density function:
which can be re-written as:
where are positive scalar parameters, and represents an arbitrary point inside the 1-simplex, . Switching the role of the parameter and the argument in this density function, we obtain:
This family is only identifiable up to the linear constraint , whence we obtain:
corresponding exactly to the continuous Bernoulli density.
Exponential distribution
[edit]An exponential distribution restricted to the unit interval is equivalent to a continuous Bernoulli distribution with appropriate[which?] parameter.
Continuous categorical distribution
[edit]The multivariate generalization of the continuous Bernoulli is called the continuous-categorical.[10]
References
[edit]- ^ Loaiza-Ganem, G., & Cunningham, J. P. (2019). The continuous Bernoulli: fixing a pervasive error in variational autoencoders. In Advances in Neural Information Processing Systems (pp. 13266-13276).
- ^ PyTorch Distributions. https://pytorch.org/docs/stable/distributions.html#continuousbernoulli
- ^ Tensorflow Probability. https://www.tensorflow.org/probability/api_docs/python/tfp/edward2/ContinuousBernoulli Archived 2020-11-25 at the Wayback Machine
- ^ Kingma, D. P., & Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
- ^ Kingma, D. P., & Welling, M. (2014, April). Stochastic gradient VB and the variational auto-encoder. In Second International Conference on Learning Representations, ICLR (Vol. 19).
- ^ Larsen, A. B. L., Sønderby, S. K., Larochelle, H., & Winther, O. (2016, June). Autoencoding beyond pixels using a learned similarity metric. In International conference on machine learning (pp. 1558-1566).
- ^ Jiang, Z., Zheng, Y., Tan, H., Tang, B., & Zhou, H. (2017, August). Variational deep embedding: an unsupervised and generative approach to clustering. In Proceedings of the 26th International Joint Conference on Artificial Intelligence (pp. 1965-1972).
- ^ PyTorch VAE tutorial: https://github.com/pytorch/examples/tree/master/vae.
- ^ Keras VAE tutorial: https://blog.keras.io/building-autoencoders-in-keras.html.
- ^ Gordon-Rodriguez, E., Loaiza-Ganem, G., & Cunningham, J. P. (2020). The continuous categorical: a novel simplex-valued exponential family. In 36th International Conference on Machine Learning, ICML 2020. International Machine Learning Society (IMLS).



![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)



![{\displaystyle \operatorname {E} [X]={\begin{cases}{\frac {1}{2}}&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {\lambda }{2\lambda -1}}+{\frac {1}{2\tanh ^{-1}(1-2\lambda )}}&{\text{ otherwise}}\end{cases}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5b1e144bd124503572e7a88169f075486059f4c)
![{\displaystyle \operatorname {var} [X]={\begin{cases}{\frac {1}{12}}&{\text{ if }}\lambda ={\frac {1}{2}}\\-{\frac {(1-\lambda )\lambda }{(1-2\lambda )^{2}}}+{\frac {1}{(2\tanh ^{-1}(1-2\lambda ))^{2}}}&{\text{ otherwise}}\end{cases}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3a107048a0d2239318adcede222d74b950cb95c)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)





![{\displaystyle x_{i}\in [0,1]\,\forall i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/494efba3aa73596741b0c462fb8863f1e531bb05)














