文：洪萬生、英家銘

4.8 電子計算機的歷史剪影

四色問題（four color problem）訴諸吾人使用地圖的日常生活經驗，本質上是拓樸學範疇的問題。我們所以留到本節才稍加說明，乃是由於它的證明主要依賴電子計算機的應用。這個問題是在1852年笛摩根致漢米爾頓的信函中指出，不過，漢米爾頓不感興趣。它針對擁有共同邊界的兩個區域不能是同色的前提下，吾人究竟需要多少種顏色，才能製作相鄰國家或地區顏色不同的地圖？至於它之所以歸屬於拓樸學，則是由於上述提問所在意的，並非地圖中區域的形狀，而是它們的圖面配置（configuration） ， 譬如哪些區域具有共同的邊界（boundary）。

這個問題所以難解，應該是圖面配置的可能性太過複雜，而且即使分類完成，著色是否只需要四種顏色就足夠，也需要龐大數量的計算。1931年美國數學家惠特尼（Hassler Whitney,1907-1989） 成功地建立了此一問題與圖論（graph theory） 的聯繫，成為後來解題的關鍵。西元1976年， 美國伊利諾大學的阿佩爾（Kenneth Appel） 與哈肯（Wolfgang Haken） 得證為四色定理（four color theorem） 。針對這個插曲，我們且看數學史家卡茲的轉述：

阿佩爾（Kenneth Appel）與哈肯（Wolfgang Haken）曾經懷疑是否能完成他們的計劃，但1976年7月24日，通過證明1936年的最後的不可避免構形的可約性，他們藉助於計算機完成了四色定理的證明。四色定理，即用四種顏色即可為任何地圖著色，首次提出於1852年7月26日。這兩個人向美國數學會提交了一份報告，該報告刊登在《美國數學會通報》（Bulletin of the American Mathematical Society） 上。

事實上，他們的證法是尋找一個由地圖所對應的圖（graph） 中可能出現的大量子圖（subgraph），然後，研究這些子圖著色的可能性。為了要在可行的時間內完成這項工作，阿佩爾和哈肯不得不大量使用計算機，持續六個月之久，使用計算機時間則超過一千個小時。數學史家卡茲也注意到：計算機自從問世以來，主要用以幫助數學家提出猜想，但在四色定理的證明中，它卻用來構造形式的證明。

不過，這種證明在數學家社群卻是「非典型」（unconventional） 的實作。數學家習慣運用最傳統的紙筆，檢視證明步驟是否在邏輯上站得住腳。這個四色定理的證明則需要吾人對於計算機計算步驟的信賴。因此，四色定理的證明是否算是一個證明？數學家社群的爭議始終未曾終止。無論如何，數學家為何要「相信」計算機這種機器？其實，吾人只須瀏覽廿世紀數理邏輯之發展，應該就可以體會：計算機有效操作所依賴的邏輯假設，絕對是主要的關鍵。因此，我們在本節中，除了介紹計算機發明的簡史之外，相關的數理邏輯之發展也打算連帶說明。

數理邏輯（mathematical logic） 與數學基礎（foundations of mathematics） 息息相關，後者誠如我們在第4.6節（有關希爾伯特23問題） 的論述所顯示，相當受到矚目，相關的問題共有第1、2、10題，足見數學基礎問題如何受到重視，更何況它們還連結到希爾伯特所主張的形式主義。譬如， 其第2題就是有關算術公理系統的相容性。這個「擬題」顯然源自他證明歐氏幾何學的相對相容性（relative consistency），亦即歐氏幾何相容若且唯若算術系統相容。

不過，此一進路受到直觀主義者布勞威爾（Brouwer） 的批判與挑戰，因此，1920年代在艾克曼（Wilhelm Ackermann,1896-1962，希爾伯特的學生）及馮紐曼（von Neumann） 完成部分成果之後，希爾伯特還是決定於1928年在波隆那舉行的ICM中，將他對數學基礎的關注，明確地以如下清晰的問題來呈現：針對算術公設系統中的一個給定的敘述，是否存在有一個標準程序， 可用以判定此敘述為真。這就是著名的判定問題（decision problem / Entscheidungsproblem） 。

對此一問題的正面解決，希爾伯特滿懷樂觀期待， 他顯然希望「一個求解他的Entscheidungsproblem之演算法，會將人類所有演繹推論化約成為粗魯的計算（brute calculation）」。而這，當然是萊布尼茲的美夢成真：因為他曾經夢想將人類理性化約成計算，也夢想一個有強大威力的機械裝置來執行計算。

西元1936年， 英國數學家圖靈（Alan Turing,1912-1954） 發表經典論文〈論可計算數，及其在判定性問題上的應用〉，為現代程式計算機奠定了基礎。他的理論建構就成為我們今日所說的圖靈機器（Turing Machine，簡稱圖靈機）。「圖靈機包括一個控制單元帶著有限多的可能狀態（state）、一張紙帶分成多個方格，以及一個帶（子）頭（tape head），其上可閱讀或書寫符號。

在計算的每一個步驟，帶頭掃描紙帶上的一個方格。根據被掃描的符號及控制單元的現在狀態（current state），圖靈機可以在現在的方格上，寫下一個新符號，將帶頭的一個方格左移或右移，如此，控制單元可能進入一個新狀態。這個新狀態可能造成停機或繼續如上程序。圖靈令人信服地論證：任意演算法程序（algorithmic procedure） 都可運用這些一系列的基本步驟來模仿。」

圖靈還「加碼」證明圖靈機可執行算術計算，然後給出一個無演算法可解的例子。這就涉及停機問題（halting problem），它是指判別一個特別的圖靈機是否會停止運算。仿照康托爾（Cantor） 的對角線論證進路，圖靈證明他的任何計算機都無法解出停機問題。他也證明任何一個停機問題的例子都可表示為數學敘述（mathematical statement）。

再者，若一個圖靈機停機，則該機之數學模仿（mathematical simulation）可證明它停機。因此， 停機問題的演算程序之不可解（algorithmic unsolvability） 就蘊含： 數學上的可證敘述（provable statement） 將會沒有判定程序。而這，當然也就證明了希爾伯特的判定問題無解了！

圖靈這一篇經典論文儘管其判定問題之解決被邏輯學家丘奇（Alonzo Church） 捷足先登，然而，它卻有如下三項極重要的貢獻：「創新定義一種抽象的計算機；證明通用計算機（universal machine） 的存在性；證明存在有任何計算機都不能解決的問題。」最後一項針對吾人直觀的計算程序之分析，尤其深具意義，因為凡是運用演算法程序（algorithmic procedure） 可計算的事物，都可以用圖靈機來計算。

總之，圖靈對電子計算機的最大貢獻，當然就是賦予當代內儲式計算機（stored­program computer） 的理論基礎。數理邏輯家戴維斯（Martin Davis） 曾經指出：「在圖靈之前，一般都認為機器、程式與資料三個範疇是全然分開的物件。機器是物理性的物件，今日我們稱之為硬體。程式是準備做計算的方案，也許體現在打孔卡或是插板上的管線之連結。

最後，資料是數值化的輸入。圖靈的通用機器顯示這三種範疇的區分只是一種錯覺。」邏輯與計算的一體兩面，引發電子計算機先驅艾肯（Howard Aiken） 在1953年給出忠實評論：「如果用來找微分方程數值解的機器，和替百貨公司開帳單的機器，在基本邏輯架構上恰好相同，我會認為這是我曾碰過的最奇妙的巧合。」

現在，讓我們回溯圖靈之前的電子計算機簡史。它的「族譜」可以追溯到十七世紀歐洲。西元1716年，納丕爾（Napier，對數發明者之一） 設計了一個可自動完成乘法計算的器械， 亦即納丕爾籌（Napier's Bones），顯然基於他所發現的對數原理。過不了多久，英國牧師奧特雷德（William Oughtred） 據以改良成為今日所稱的對數尺，成為迄至廿世紀中葉工程師的必備計算工具之一。

另一方面，法國的巴斯卡（Pascal） 也在1642-1652年間發明「加法機」，可以「自動」操作加減計算，數目相加減時，只需將數目鍵入，而這臺機器就會代勞其餘部分。不過，這些製作全賴手工，以萊布尼茲（Leibniz） 基於二進位算術原理，而發明的「步進計算器」（stepped reckoner），就因為工匠技術還不足以有效地承造這一設計的可靠複件，而使得商品化的時機推遲了一百五十年以上。

到了十九世紀早期，劍橋數學家巴貝吉（Charles Babage） 設計一種可造對數表與天文數表的機器。由於它對航海大有助益，因此，英國政府開始提供贊助。西元1822年， 他在「差分機」（Difference Machine） 上不停操作運算，造出一種具有六位數準確的數表。在這個基礎上，他向準確到二十位數的目標前進，這個計畫並未成功，於是，英國政府就不再贊助。

西元1833年，巴貝吉提出更有野心的「分析機」（Analytical Engine） 。由於法國工程師雅各（Joseph­Marie Jacquard） 有關織布機中，編織複雜類型中的一系列打孔卡片之「前程式化」（pre­programed） 設計，引導巴貝吉嘗試打造一個可以從打孔的卡片接收與描述數據的機械，而這就是他所謂的分析機。

巴貝吉的計畫中有一位助手十分有名， 她就是艾達羅夫萊斯（Ada Lovelace），詩人拜倫（Byron） 的女兒、數學家笛摩根的學生。她將巴貝吉在1840年於義大利召開的有關分析機實用性的研討會論文，翻譯成英文並補充她自己的註釋，其中她擴張了「編制程式」的想法到配備有打孔卡片的機器上，並且寫下史上第一個有意義的計算機程式，預見了許多包括重複步驟的一個「迴路」之現代編制程式設計。

儘管如此，分析機被十九世紀的技術所限，無法製造出來。在一百多年後，巴貝吉及艾達的想法被廿世紀的計算機製造者重新發現。不過，在十九世紀中葉，自修成才的數學家布爾（George Boole） 在他的兩部數理邏輯著作中，「說明基本邏輯程序如何可以利用現在稱為布爾代數（Boolean algebra） 的系統，表示成為1和0的組合。」事實上，「布爾代數已經成為今日計算機所有的『思考』電路設計之理論鑰匙。」

在技術方面， 十九世紀還有一項不可或缺的發明， 那就是， 在1880年，美國人口普查局的年輕員工海倫里斯（Herman Hollerith） 設計了一種機器，可使用電力自動地對記錄在打了孔洞的卡片上之數據，進行分類與製表，這大幅地縮短處理數據的時間。海倫里斯後來創辦製表機器公司（Tabulating Machine Company），最後發展成為今日的工業巨擘IBM。

西元1937年， 夏農（Claude Shannon） 在他的MIT碩士論文中，結合布爾代數及電力繼電器和開關電路，顯示機器能夠「做」數學邏輯。所有這些關鍵因素都在這個時候集結在一起，其中當然包括圖靈在1936年所發表的經典論文。夏農的這一篇論文「將數位迴路設計從技術轉換成為科學」， 因此， 他所創立的資訊之數學理論（mathematical theory of information），在當代通訊技術發展上，扮演關鍵的角色。

當第二次世界大戰爆發時，敵對雙方都企圖通過技術研究，以掌握軍事優勢，圖靈就是因此而涉入破解德軍密碼的情報工作。同樣涉入數學的軍事技術的數學家， 還有匈牙利出身的傑出數學家馮紐曼（von Neumann）。他在1931年移民美國。二次戰後，馮紐曼除了繼續任職於普林斯頓高級研究院（Institute of Advance Study） 之外，還被邀請充當電子數值積分計算器（ENIAC） 的數學顧問。

ENIAC （Electronic Numerical Integrator and Calculator） 主要由賓州大學的艾克特（Eckert）與馬科林（Mauchly） 負責建造， 其目的是幫助美國計算海軍大砲射程圖。由於使用多達18000個真空管、1500個繼電器等等，重量超過三十噸，體積龐大笨重。不過，馮紐曼的真正貢獻是在於他發明一種在計算機內儲存程式的方法，其設計建造圖可以參考圖4.5。1949年，他的機器建造設計在英國劍橋大學所製造的EDSAC （Electronic Delayed Storage Automatic Computer） 上，首度得以運算操作。

前述龐大笨重的計算器所費不貲，因此，在技術創新的需求下，貝爾實驗室（Bell Lab） 在1950年代早期發明的電晶體，將電子計算機推進到第二代的更小、更快以及更有威力，而且也更具經濟性。第三代則是在1960年代中期因積體電路之引進而降臨，個人電腦也成為一般人負擔得起的現實：從迷你型縮小到微小型、再到桌上型、到膝上型，最後到掌上型，甚至到二十一世紀智慧型手機，所有這些都見證電子計算機時代的無限風華。

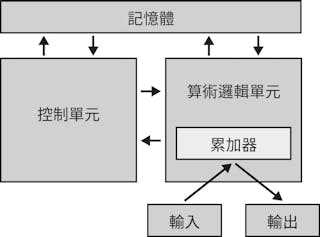
圖4.5：馮紐曼機器的建造設計圖

Photo Credit: 三民出版

圖4.5：馮紐曼機器的建造設計圖

書籍介紹

本文摘錄自《數之軌跡Ⅳ：再度邁向顛峰的數學》，三民出版

編者：洪萬生、英家銘

  • momo網路書店
  • Readmoo讀墨電子書
  • Pubu電子書城結帳時輸入TNL83，可享全站83折優惠（部分商品除外，如實體、成人及指定優惠商品，不得與其他優惠併用）
  • 透過以上連結購書，《關鍵評論網》將由此獲得分潤收益。

臺灣數學界的《史記》，臺灣數學史研究第一人洪萬生心血之作

柏拉圖將五元素連結五種正多面體的圖形，
讓古希臘宇宙論有了最自然的「數學歸宿」。

以五元素中的四個古典元素為靈感，《數之軌跡》將深入探索數學的歷史、發展和奧祕。每本書都是一個獨特的元素，象徵不同的數學主題，並呈現數學在文化、科學和藝術中的深遠影響。

無論你是一位數學愛好者、學生還是對數學歷史感興趣的讀者，《數之軌跡》都將為你打開數學的大門，啟發你對這一古老而美麗的學科有新見解。

再度邁向顛峰的數學
風象徵著數學的抽象和邏輯思維，也是多面而有序的正八面體。
這本書將進入數學的抽象世界，從形式邏輯到代數與幾何的奧祕。深入了解數學家如何思考與探究抽象概念，將它們應用於解決現實的難題，打破抽象數學的框架。同時引領讀者藉由近代數學家的研究結晶，發現從數學到現代科技的無限可能與未來發展。

閱讀歷史，體會數學
「阿涅西的女巫」這個名稱聽起來奇幻又美麗，然而，它實際上是一條數學曲線──箕舌線。這個名稱源自於翻譯時的小誤會，卻讓這條曲線增添更多的神祕色彩。
法國數學家究竟如何面對「不確定性」的科學？拉普拉斯透過信念，對於「機械決定論」有著無比的信心。他想像有一個像上帝一樣全知全能的存在，能夠追蹤宇宙中每一個原子的位置，以及作用在原子的所有力，這樣的假想如今被稱為「拉普拉斯的惡魔」。

通往數學思維的大門
不僅僅是闡述數學歷史，更能幫助讀者理解數學的抽象概念，理解數學背後的邏輯推演。內容探索各種古代人的智慧，無論是否喜歡數學，都能從中發現數學的樂趣以及實用性，對學習數學將會有非常大的幫助！

本書特色

  • 數學史大師洪萬生與HPM團隊共同打造最全面的數學歷史
  • 多元歷史題材，對比不同文明之間有關同一知識內容的研究
  • 深入探討文化差異，參悟不同命題與證明的數學風格

Photo Credit: 三民出版

【加入關鍵評論網會員】每天精彩好文直送你的信箱，每週獨享編輯精選、時事精選、藝文週報等特製電子報。還可留言與作者、記者、編輯討論文章內容。立刻點擊免費加入會員！

責任編輯：翁世航
核稿編輯：馮冠維