Heap

 Nota: Para a área de memória dinâmica, veja Gerenciamento de memória.

Exemplo de uma heap máxima binária com chaves de nó sendo inteiros de 1 a 100

Em ciência da computação, um heap (monte) (pronuncia-se riːp) é uma estrutura de dados especializada, baseada em árvore, que é essencialmente uma árvore quase completa que satisfaz a propriedade heap: se P é um nó pai de C, então a chave (o valor) de P é maior que ou igual a (em uma heap máxima) ou menor que ou igual a (em uma heap mínima) chave de C. O nó no "topo" da heap (sem pais) é chamado de nó raiz.

O heap é uma implementação maximamente eficiente de um tipo de dados abstrato chamado de fila de prioridade e, de fato, as filas de prioridade são geralmente chamadas de "heaps", independentemente de como elas podem ser implementadas. Em uma heap, o elemento de prioridade mais alta (ou mais baixa) é sempre armazenado na raiz. No entanto, uma heap não é uma estrutura classificada, ela pode ser considerada parcialmente ordenada. Uma heap é uma estrutura de dados útil quando é necessário remover repetidamente o objeto com a prioridade mais alta (ou mais baixa).

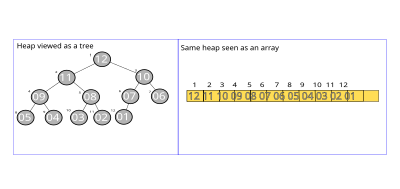
Uma implementação comum de uma heap é a heap binária, no qual a árvore é uma árvore binária (veja a figura). A estrutura de dados da heap, especificamente a heap binária, foi introduzida por J. W. J. Williams em 1964, como uma estrutura de dados para o algoritmo de classificação heapsort. Heaps também são cruciais em vários algoritmos de grafo eficientes, como o algoritmo de Dijkstra. Quando uma heap é uma árvore binária completa, ela possui a menor altura possível - uma heap com N nós e, para cada nó, a ramos, sempre possui altura de log_aN.

Observe que, conforme mostrado no gráfico, não há ordenação implícita entre irmãos ou primos e nenhuma sequência implícita para um percurso em ordem (como haveria, por exemplo, uma árvore de pesquisa binária). A relação de heap mencionada acima se aplica somente entre nós e seus pais, avós, etc. O número máximo de filhos que cada nó pode ter depende do tipo de heap.

Exemplos

// Seja i o índice de um dado elemento da heap. Podem ser facilmente encontradas referências aos
// elementos a ele conectados (pai e filhos) através das seguintes relações:
PAI = (i-1)/2
ESQUERDA = 2*i+1
DIREITA = 2*i+2
// Onde i é o inde atual, e o resulta da operação é o índice desejado

Um arranjo acessado como uma arvore binaria balanceada.

Uma boa implementação de ordenação por heap geralmente implementa as instruções dispostas anteriormente como macros, como consequência, a implementação dessas operações podem ser executadas rapidamente (ver operações bit a bit). Para o filho esquerdo desloca os bits a esquerda, para o direito desloca os bits a direita e aplica a operação "ou" com 1. Para encontrar o pai, desloca um bit a direita. A vantagem de usar operações bit a bit, é que cada uma delas usa apenas um ciclo de clock do processador, sendo altamente eficiente.

Características

Existem dois tipos de heaps: Os heaps de máximo (max heap), em que o valor de todos os nós são menores que os de seus respectivos pais; e os heaps de mínimo (min heap), em que o valor de todos os nós são maiores que os de seus respectivos pais. Assim, em um heap de máximo, o maior valor do conjunto está na raiz da árvore, enquanto no heap de mínimo a raiz armazena o menor valor existente.

De maneira geral, um heap é uma forma eficiente de implementação de uma fila de prioridade, uma vez que o elemento de maior ou menor valor sempre está armazenado na primeira posição e que a remoção sempre é feita nesse mesmo elemento.

A árvore binária do heap deve estar completa até pelo menos seu penúltimo nível e, se o seu último nível não estiver completo, todos os nós do último nível deverão estar agrupados à esquerda. Assim, as inserções em uma heap são feitas sequencialmente no array em que esta é implementada, com certas manipulações para a manutenção de suas propriedades, além disto as inserções são sempre feitas nas folhas, mais precisamente na folha livre mais à esquerda, essa inserção pode não respeitar as invariantes da heap, por isso é necessário um processo chamado heapify após a inserção para garantir que as invariantes sejam mantidas.

Considerando $n$ como o número de elementos de um heap, inserção e remoção têm complexidade da ordem $O(log(n))$.

Operações

As operações mais comuns em heaps são:

GetParent

Considerando que heap é um array e que a posição de um nó é i, a posição do seu pai será (i - 1) / 2.

private int parent(int i) {
	return (i - 1) / 2;
}

GetRight

Considerando que heap é um array e que a posição de um nó é i, a posição do seu filho da direita será (i * 2 + 1) + 1.

private int right(int i) {
	return (i * 2 + 1) + 1 ;
}

GetLeft

Considerando que heap é um array e que a posição de um nó é i, a posição do seu filho da esquerda será (i * 2 + 1).

private int left(int i) {
	return (i * 2 + 1);
}

Inserção

• Inserção: Adiciona um novo nó ao heap.

Código em Java

public void insertItem(Object k, Object e) throws InvalidKeyException {
    if(!comp.isComparable(k))
        throw new InvalidKeyException("Invalid Key");
    Position z = T.add(new Item(k, e));
    Position u;
    while(!T.isRoot(z)) { // vai levando o elemento para cima até chegar ao seu lugar correto
        u = T.parent(z);
        if(comp.isLessThanOrEqualTo(key(u),key(z)))
             break;
        T.swapElements(u, z);
        z = u;
     }
}

Remoção

• Remoção: Remove o elemento da raiz do heap; em geral, troca-se o elemento na última posição com a raiz, diminui-se a referência à última posição armazenada e então são feitas alterações de forma a preservar os invariantes do heap.

Código em Java

public Object removeMin() throws PriorityQueueEmptyException {
    if(isEmpty())
        throw new PriorityQueueEmptyException("Priority Queue Empty!");
    Object min = element(T.root());
    if(size() == 1)
        T.remove();
    else {
        T.replaceElement(T.root(), T.remove());
        Position r = T.root();
        while(T.isInternal(T.leftChild(r))) {
            Position s;
            if(T.isExternal(T.rightChild(r)) || comp.isLessThanOrEqualTo(key(T.leftChild(r)),key(T.rightChild(r))))
                s = T.leftChild(r);
            else
                s = T.rightChild(r);
            if(comp.isLessThan(key(s), key(r))) {
                T.swapElements(r, s);
                r = s;
            }
            else
                break;
        }
    }
}

Build Heap

• Build heap: Constrói o heap a partir de um array desordenado, fazendo uso da operação de heapify diversas vezes para preservar os invariantes da estrutura.
• Primeiramente iteramos da metade do array ao começo, pois teremos apenas índices válidos para filho a esquerda e filho a direita, próximos a metade.

Código em Java:

public void buildHeap(Object[] array) {
    this.array = array;

    for (int i = parent(lastIndex) / 2; i >= 0; i--) { // Inicia no pai do último elemento.
        heapify(i);
    }
}

Heapify

• Heapify: Em síntese, o heapify é uma operação que visa manter a invariante de um dado heap. Em um max heap, por exemplo, o heapify garante que os filhos de cada nó sejam menores ou iguais ao pai.

heapify(A,i)
    l = left(i)
    r = right(i)
    if l <= heap-size[A] and A[l] > A[i]
        then largest = l
        else largest = i
    if r <= heap-size[A] and A[r] > A[largest]
        then largest = r
    if largest ≠ i
        then exchange A[i] <--> A[largest]
            heapify(A,largest)

Basicamente este código irá descer o valor até o seu lugar apropriado na arvore, de forma a manter as invariantes. Este é utilizado na remoção com muita frequência.

Heapsort

• Heapsort: O heapsort é uma técnica de ordenação que se aproveita da característica da heap em que sempre o menor ou maior elemento (dependendo do tipo da heap) deve estar na raiz, para ordenar os dados. Pode ser aplicado in place em um max heap ou através de consecutivas remoções em um min heap.
• Tendo em vista que as remoções na heap levam O(log(n)) e para ordenar n elementos seriam necessárias n remoções, temos que o tempo médio do heapsort é O(nlog(n)), onde n é quantidade de elementos. Este tempo é semelhante a algoritmos como mergesort e quicksort, entretanto, uma boa implementação de quicksort ainda se mostra superior.

Implementação em Java

• public T[] heapsort(T[] array) {
  	T[] result = array;
  	if (array.length > 1) {
  		buildHeap(array);
  		for (int i = array.length - 1; i >= 0; i--) {
  			Util.swap(heap, 0, i);
  			index--;
  			heapify(0);
  		}
  		result = heap;
  		if (heap[0].compareTo(heap[1]) > 0) {
  			T[] inverse = util.Util.makeArrayOfComparable(array.length);
  			for (int i = 0; i < array.length; i++) {
  				inverse[i] = heap[array.length - 1 - i];
  			}
  			result = inverse;
  		}
  	}
  	return result;
  }
  

Merge

Merge (união): O método tem como objetivo juntar duas heaps retornando e transformando em uma só. Sendo uma heap representada por um array, o arrayA e o arrayB, que são as heaps que serão unidas com o objetivo de transformar-se em uma só, chamada no código de "newHeap".

Implementação em Java

• public int[] merge(int[] arrayA, int[] arrayB) {
  	for (int element : arrayA) {
  		insert(element);
  	}
  	for (int element : arrayB) {
  		insert(element);
  	}
  
  	int[] newHeap = new int[size()];
  
  	for (int index = 0; index < newHeap.length; index++) {
  		newHeap[index] = extractRootElement();
  	}
  	return newHeap;
  }
  

Estatística de Ordem

• A n-ésima estatística de ordem de uma heap é o n-ésimo menor elemento da estrutura. Tendo como exemplo a seguinte min heap: [1, 6, 58, 12, 34, 64, 99, 82]; o elemento que tem estatística de ordem igual a 3 é o número 12, pois o mesmo é o 3º menor elemento da heap.

Considerando uma min heap, para procurar o elemento que possui a n-ésima estatística de ordem, basta considerar o seguinte código em Java:

public T estatisticaDeOrdem(int n) {
	T n_Element = null;
		
	while(n > 0 && n <= this.index) {
		n_Element = extractRootElement();
		n--;
	}
		
	return n_Element;
}

Encaminhamento em Largura (BFS)

Breadth-first search (BFS) ou Encaminhamento em Largura é uma forma de percorrer uma árvore visitando os nós vizinhos de um determinado nível desta árvore.

Ilustração para BFS

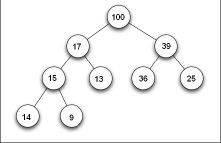
Por exemplo na Max-Heap à direita, percebe-se que ao analisar a Heap em sua largura, temos 4 níveis, o 1° com o valor 100, o 2° com os seguintes valores: 17, 39 e assim sucessivamente.

public List<T> BFS(int level) {
    if (level > this.index || level < 0) {
        throw new RuntimeException("Level inexistente");
    }

    int comecoLevel = (int) (Math.pow(2, level) - 1);
    int levelFinal = comecoLevel * 2;
    List<T> elementosPorLevel = new ArrayList<T>();

    for (int i = comecoLevel; i <= levelFinal; i++) {
        elementosPorLevel.add(heap[i]);
    }

    return elementosPorLevel;

}

Implementações

Heaps podem ser implementados para fornecer o menor valor (heaps de mínimo ou min heap) ou o maior valor (heaps de máximo ou max heap). Nesse quesito, as implementações podem variar. Podem ser generalizados, entretanto, através do uso de um Comparator em Java, por exemplo, que se adaptam à situação. Outra variação comum está no index do elemento raiz (o menor elemento do heap, se for um heap de mínimo, ou o maior, se for um heap de máximo): enquanto algumas implementações optam por usar o index 0 do arranjo como raiz, outras optam por usar o index 1. Essa variação altera as operações de obter os filhos a partir do pai, e de obter o pai a partir de um dos filhos.

Implementação em C++

// Quanto à mistura de idiomas, os métodos privados estão em português apenas para facilitar o entendimento.

template<class T>
class BinaryMinHeap
{
	// Usamos um vector<T>, em vez de um T* heap, para não termos que nos preocupar com alocação de memória
	vector<T> heap;

	inline int filhoE(int i) { return i<<1; } // (i<<1) é similar a (i*2)
	inline int filhoD(int i) { return (i<<1)|1; } // ((i<<1)|1) é similar a ((i*2)+1)
	inline int pai(int i) { return i>>1; } // (i>>1) é similar a (i/2)

	void corrigeSubindo(int index)
	{
		// Enquanto o valor do filho for menor do que o valor do pai, troca o pai com o filho e sobe
		for (; index > 1 && heap[index] < heap[pai(index)]; index = pai(index))
			swap(heap[index], heap[pai(index)]);
	}

	void corrigeDescendo(int index=1) // também conhecida como heapify(index)
	{
		// Repete enquanto index ainda tiver filho
		while (filhoE(index) < heap.size())
		{
			// Seleciona o filho com menor valor (esquerda ou direita?)
			int filho = filhoE(index);
			if (filhoD(index) < heap.size() && heap[filhoD(index)] < heap[filhoE(index)])
				filho = filhoD(index);

			// Se o valor do pai é menor do que o valor do menor filho, terminamos
			if (heap[index] < heap[filho])
				break;

			// Caso contrário, trocamos o pai com o filho no heap e corrigimos agora para o filho
			swap(heap[index], heap[filho]);
			index = filho;
		}
	}

public:
	BinaryMinHeap() { T nil; heap.push_back(nil); }
	inline T& top() { return heap[1]; }
	inline int size() { return heap.size() - 1; }
	inline bool empty() { return heap.size() <= 1; }

	void push(T v)
	{
		heap.push_back(v);
		corrigeSubindo(size());
	}

	void pop()
	{
		if (heap.size() > 1)
		{
			swap(heap[1], heap.back());
			heap.pop_back();
			corrigeDescendo();
		}
	}

	void buildHeap(vector<T>& array)
	{
		// Copia o array recebido para o array do heap
		T nil;
		heap.clear();
		heap.push_back(nil);
		for (int i = 0; i < array.size(); i++)
			heap.push_back(array[i]);

		// Constrói o heap
		for (int index = size()/2; index; index--)
			corrigeDescendo(index);
	}
};

Os métodos mais importantes na implementação são o corrigeSubindo e o corrigeDescendo. O primeiro corrige o heap para um determinado índice recém-adicionado. É utilizado na inserção, pois para inserir um elemento em um heap podemos simplesmente adicioná-lo no final do arranjo, e depois empurrá-lo para cima na árvore enquanto ele for menor que o pai (ou maior, se for um heap de máximo). Já o corrigeDescendo realiza o mesmo processo, mas é utilizado quando o elemento precisa ser empurrado para baixo, e não para cima. Isso acontece na remoção, pois nesta operação selecionamos o último elemento do arranjo e trocamos com a raiz. Assim, podemos descartar a raiz (que está no final do arranjo agora, bastando remover o último elemento do arranjo). Porém, o último elemento do arranjo (que foi movido para a raiz) provavelmente não é o menor, e a raiz deve sempre guardar o menor elemento. Portanto, devemos empurrar o elemento para baixo até que o heap esteja corrigido. Segue uma implementação recursiva dessas duas funções:

	void corrigeSubindo(int index)
	{
		// Se index não é a raiz e o valor do index for menor do que o valor de seu pai,
		// troca seus valores (index e pai(index)) e corrige para o pai
		if (index > 1 && heap[index] < heap[pai(index)])
		{
			swap(heap[index], heap[pai(index)]);
			corrigeSubindo(pai(index));
		}
	}

	void corrigeDescendo(int index=1)
	{
		// Se index tem filho
		if (filhoE(index) < heap.size())
		{
			// Seleciona o filho com menor valor (esquerda ou direita?)
			int filho = filhoE(index);
			if (filhoD(index) < heap.size() && heap[filhoD(index)] < heap[filhoE(index)])
				filho = filhoD(index);

			// Se o valor do pai é menor do que o valor do menor filho, terminamos
			if (heap[index] < heap[filho])
				return;

			// Caso contrário, trocamos o pai com o filho no heap e corrigimos agora para o filho
			swap(heap[index], heap[filho]);
			corrigeDescendo(filho);
		}
	}

Implementação em Java

A classe abaixo escrita em java contém o código de uma heap de seus comportamentos. É utilizado um tipo de dado genérico (generics), para que esta implementação esteja preparada para diversos tipo de objetos. Utiliza-se ainda um comparador (comparator), este é responsável por definir qual o tipo da heap, minima ou máxima.

public class HeapImpl<T extends Comparable<T>> {

	protected T[] heap;
	protected int index = -1;
	private static int ZERO = 0;
	/**
	 * O comparador é utilizado para fazer as comparações da heap. O ideal é
	 * mudar apenas o comparator e mandar reordenar a heap usando esse
	 * comparator. Assim os metodos da heap não precisam saber se vai funcionar
	 * como max-heap ou min-heap.
	 */
	protected Comparator<T> comparator;

	private static final int INITIAL_SIZE = 20;
	private static final int INCREASING_FACTOR = 10;

	public HeapImpl(Comparator<T> comparator) {
		this.heap = (T[]) (new Comparable[INITIAL_SIZE]);
		this.comparator = comparator;
	}

	private int parent(int i) {

		int x = (i - 1) / 2;
		return x;
	}

	/**
	 * Deve retornar o indice que representa o filho a esquerda do elemento
	 * indexado pela posição i no vetor
	 */
	private int left(int i) {
		return (i * 2 + 1);
	}

	/**
	 * Deve retornar o indice que representa o filho a direita do elemento
	 * indexado pela posição i no vetor
	 */
	private int right(int i) {
		return (i * 2 + 1) + 1;
	}

	public boolean isEmpty() {
		return (index == -1);
	}

	public T[] toArray() {
		T[] resp = Util.makeArrayOfComparable(index + 1);
		for (int i = 0; i <= index; i++) {
			resp[i] = this.heap[i];
		}
		return resp;
	}

	/**
	 * Valida o invariante de uma heap a partir de determinada posição, que pode
	 * ser a raiz da heap ou de uma sub-heap. O heapify deve colocar os maiores
	 * (comparados usando o comparator) elementos na parte de cima da heap.
	 */
	private void heapify(int position) {
		if (position == ZERO) { // Remove
			heapfyDown(ZERO);
		} else { // Insert
			heapfyUp(position);
		}
	}

	/**
	 * Faz o processo de Heapfy de cima para baixo, levando o elemento
	 * adicionado na raiz para aposição correta
	 */
	private void heapfyDown(int index) {
		int rightIndex = this.right(index);
		int leftIndex = this.left(index);
		int largest;

		if (leftIndex <= this.index && this.biggerElement(leftIndex, rightIndex) == leftIndex) {
			largest = leftIndex;
		} else {
			largest = index;
		}

		if (rightIndex <= this.index && this.biggerElement(rightIndex, largest) == rightIndex) {
			largest = rightIndex;
		}

		if (largest != index) {
			Util.swap(this.getHeap(), index, largest);
			this.heapfyDown(largest);
		}
	}

	/**
	 * Faz o processo de Heapfy de baixo para cima, levando o elemento
	 * adicionado para aposição correta
	 */
	private void heapfyUp(int position) {
		int currentIndex = position;

		while (this.biggerElement(currentIndex, this.parent(currentIndex)) == currentIndex
				&& this.parent(currentIndex) != currentIndex) {
			Util.swap(this.getHeap(), currentIndex, this.parent(currentIndex));
			currentIndex = this.parent(currentIndex);
		}

	}

	/**
	 * Verifica qual o maior elemento com base e seu indice e retorna o indice
	 * do mesmo
    */
	private int biggerElement(int IndexOfElem1, int IndexOfElem2) {
		if (this.comparator.compare(this.getHeap()[IndexOfElem1], this.getHeap()[IndexOfElem2]) > ZERO)
			return IndexOfElem1;
		else
			return IndexOfElem2;
	}

	public void insert(T element) {
		if (element != null) {

			if (index == heap.length - 1) {
				heap = Arrays.copyOf(heap, heap.length + INCREASING_FACTOR);
			}

			this.getHeap()[++this.index] = element;
			this.heapify(this.index);
		}
	}

	public void buildHeap(T[] array) {
		if (array != null & array.length > 0) {
			this.heap = (T[]) new Comparable[array.length];

			this.index = -1;

			for (int i = 0; i < array.length; i++) {
				if (array[i] != null)
					this.insert(array[i]);
			}

		}
	}
	
	public T extractRootElement() {
		T root = null;

		if (!this.isEmpty()) {
			root = this.getHeap()[ZERO];
			this.getHeap()[ZERO] = this.getHeap()[this.index];
			this.index--;
			this.heapify(ZERO);
		}

		return root;
	}

	public T rootElement() {
		T root = null;

		if (!this.isEmpty()) {
			root = this.getHeap()[ZERO];
		}

		return root;
	}

	@Override
	public T[] heapsort(T[] array) {
		Comparator<T> comparatorOriginal = this.comparator;

		this.setComparator((o1, o2) -> o1.compareTo(o2));
		this.buildHeap(array);

		T[] heapSorted = Util.makeArrayOfComparable(this.size());

		for (int i = this.index; i >= 0; i--) {
			heapSorted[i] = this.extractRootElement();
		}

		this.setComparator(comparatorOriginal);
		return heapSorted;

	}

	public int size() {
		return this.index + 1;
	}

	public Comparator<T> getComparator() {
		return comparator;
	}

	public void setComparator(Comparator<T> comparator) {
		this.comparator = comparator;
	}

	public T[] getHeap() {
		return heap;
	}
}

Utilização

Uma das utilizações mais tradicionais do heap é no algoritmo de ordenação heapsort, que utiliza a propriedade do heap de o maior (ou menor valor) localizar-se na raiz do mesmo e fazer a ordenação dos dados de uma maneira bastante eficiente.

Também pode ser usada como heaps de prioridades onde a raiz é a maior prioridade.

Outra utilização de heaps são em algoritmos de seleção. Operações de encontrar o maior, ou menor, elemento de um conjunto de números é realizado de uma forma bastante eficiente, em comparação com a utilização de uma lista ligada ordenada.

Ver também

• Heapsort
• Árvores

Bibliografia

• Cormen, T.H.; et al. (2001). Introduction to algorithms. [S.l.]: The MIT press