JP4281419B2 - 前置型非線形歪補償器 - Google Patents
前置型非線形歪補償器 Download PDFInfo
- Publication number
- JP4281419B2 JP4281419B2 JP2003157249A JP2003157249A JP4281419B2 JP 4281419 B2 JP4281419 B2 JP 4281419B2 JP 2003157249 A JP2003157249 A JP 2003157249A JP 2003157249 A JP2003157249 A JP 2003157249A JP 4281419 B2 JP4281419 B2 JP 4281419B2
- Authority
- JP
- Japan
- Prior art keywords
- support vector
- signal
- coefficient
- data
- vector
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Expired - Fee Related
Links
Images
Landscapes
- Amplifiers (AREA)
Description
【発明の属する技術分野】
本発明は、前置型非線形歪補償器に関し、特に、サポートベクトルマシン(以下「SVM」という)を回帰分析に用いた前置型非線形歪補償器に関する。
【0002】
【従来の技術】
近年、通信における非線形デバイス(以下「NLD」という)の非線形歪を補償する技術として、前置型非線形歪補償器が注目されている。代表的な前置型非線形歪補償器として、ルックアップテーブルを用いたものと、NLDの逆特性を推定するものがある。ここで、NLDの典型的なものとしては、たとえば、増幅器が挙げられる。
【0003】
ルックアップテーブルを用いた前置型非線形歪補償器は、増幅器の特性を入力信号の振幅値に対して微小区間に分け、その区間の代表値をテーブルに格納しておき、送信信号とそれに対応するテーブルの補償値を乗算して出力信号とするものである。また、前置型非線形歪補償器入力とNLD出力を比較し、その結果から適応的にテーブル内の補償値を更新する前置型非線形歪補償器も既に開発されている。
【0004】
一方、増幅器の逆関数を推定する前置型非線形歪補償器として、pth−order−predistorterと呼ばれるものがある。この前置型非線形歪補償器は、信号変換器の逆関数を複素多項式近似するものである。複素多項式は、非線形関数の表現形式として最も一般的なボルテラ級数より導出され、歪補償が行なわれる。また、前置型非線形歪補償器入力とNLD出力を比較し、その結果から適応的に複素多項式係数を更新する前置型非線形歪補償器も既に開発されている。
【0005】
しかし、ルックアップテーブルを用いた前置型非線形歪補償器では、テーブル内の値は離散値をとるため、値の不連続性により、フロアノイズが上昇する。フロアノイズを解消するためには、データ数を増やす必要があるが、データ数を増やすとメモリ容量が多くなるという問題がある。
【0006】
pth−order−predistorterでは、計算精度を上げるために複素多項式の次数を増やす必要がある。このため、計算時間がかかり、解が収束しにくいという問題がある。
【0007】
さらに、広帯域信号に対しては、ルックアップテーブル、pth−order−predistorterともに、信号帯域内の各周波数ごとに振幅、位相の非線形性を補償する必要があるため、ハードウェア化が困難であるという問題がある。
【0008】
ところで、近年、入出力観測データからプロセスのモデリングを行うという問題は、非線形回帰問題やシステム同定などの多くの分野において研究の目的となっている。上記前置型非線形歪補償器の最適な特性を得るという問題も、ひずみを補償する対象となる増幅器を未知の非線形システムとみなせば、この補償する対象となる増幅器の特性の逆関数のモデリングの問題に帰着される。
【0009】
このようなプロセスモデリングの問題に取り組む方法は、大きく分けてグローバルモデリングとローカルモデリングの2つに分けることができる。
【0010】
ローカルモデリングは、重み平均法、局所重み回帰法やデータベース学習であるJust-in-time法などがある。
【0011】
これに対して、グローバルモデリングは、データベースの全てに適合する一つの関数を作る手法である。このような関数の作成は、ニューラルネットワークモデリングや非線型統計回帰の他の方法で使われている手法である。
【0012】
このようなグローバルモデリングに対する統計的学習理論は、1960年代から存在していたが、実用的なツールとして用いられるようになったのは、1990年半ば以降にV.N.Vapnik等によって、サポートベクトルマシンが提案されたことを契機とする(たとえば、非特許文献1〜3を参照)。
【0013】
このようなサポートベクトルマシンを用いた統計的学習理論によるプロセスモデリングには、一般的に、以下のような特徴がある。
【0014】
(1)他の手法に比べると、収束速度に勝る。
(2)常に唯一の解を得ることができる。
【0015】
(3)さまざまな学習問題に容易に適用できる。
(4)問題の複雑さを問題の次元とは独立であるサポートベクトルの個数によって特徴づけているために、いわゆる「次元の呪い(curse of dimensionality)」から逃れることができる。
【0016】
さらに、上述したサポートベクトルマシンは、回帰問題の学習に用いることのできるサポートベクトル回帰(Support Vector Regression(以下、「SVR」と呼ぶ))に拡張されている。このようなSVRについては、非特許文献4に開示がある。
【0017】
さらに、このようなサポートベクトルマシンを上述した前置型非線形歪補償器に適用する試みが、非特許文献5に開示されている。
【0018】
【非特許文献1】
V.N.Vapnik : The Nature of Statistical Learning Theory, Springer-Verlag, New York(1995)
【0019】
【非特許文献2】
V.N.Vapnik : Statistical Learning Theory, J.Willey & Sons, New York(1998)
【0020】
【非特許文献3】
B.Scholkopf et al.ed, "Advances in Kernal Methods", The MIT Press, 1999.
【0021】
【非特許文献4】
N.Cristianini, J.Shave-Taylor "An Introduction to Support Vector Machines", Cambridge University Press, 2000.
【0022】
【非特許文献5】
伊藤隆徳,大森浩充,佐野昭 B−5−124「サポートベクトル法を用いた適応非線形歪補償」2001年電子情報通信学会総合大会予稿集、p.522,2001年
【0023】
【発明が解決しようとする課題】
しかしながら、サポートベクトルマシンをデジタル信号受信装置の前置型非線形歪補償器に用いる場合には、以下のような点を考慮する必要がある。
【0024】
ここで、通信に利用されるNLDのうち、最も伝送特性に影響を及ぼすのは増幅器である。
【0025】
図20は、一般な増幅器の入出力特性を示す図である。
図20に示すように、入力信号が小さい領域では線形的に動作するが、入力信号が大きくなるにつれて出力信号は飽和する。
【0026】
通常は、このような増幅器の非線形歪による影響を軽減するために、増幅器に対してマージンを設定し、その分だけ増幅器への入力レベルを下げて動作させる。このマージンを「バックオフ」と呼ぶ。
【0027】
所要バックオフの大きさは変調方式に依存する。たとえば、変調方式がπ/4シフトQPSK(Quadrature Phase Shift Keying)であれば、振幅変動が小さいのでバックオフは小さくてもよい。しかしながら、たとえば変調方式が直交周波数分割多重(以下「OFDM(Orthogonal Frequency Division Multiplexing)」という)であれば、振幅変動が大きいのでバックオフを大きく設定する必要がある。
【0028】
ところが、バックオフを大きく設定すると、増幅器の電力効率が大幅に劣化してしまう。そこで、信号のような振幅変動が大きい信号に対しても、なるべく小さいバックオフで動作させるのが望ましい。
【0029】
しかしながら、バックオフを小さく設定すると、SVRのようなグローバルモデリングを用いた前置型非線形歪補償器では、補償できないほどに過剰に大きな歪を有する信号が、前置型非線形歪補償器に入力されることになる。
【0030】
ここで、増幅器の逆特性、すなわち理想的に動作する前置型非線形歪補償器の特性は、図20に示すとおりである。ここで、前置型非線形歪補償器の出力は、入力が大きい場合に非常に大きくなってしまう。これは同時に、また増幅器への入力自体が非常に大きくなることを意味する。
【0031】
ただし、このように大きな入力が仮に増幅器に入力されても、増幅器の特性自体が飽和しているので、もはや、前置型非線形歪補償器では、補償を行なうことができない。この場合、特に、SVRのように補償動作を学習するようなシステムでは、有効な学習ができなくなるという問題が生じる。
【0032】
本発明は、上述の課題を解決するためになされたもので、その目的は、振幅変動が大きい信号に対してもなるべく小さいバックオフで動作可能であり、なおかつ高精度で歪補償を可能とする前置型非線形歪補償器を提供することである。
【0033】
【課題を解決するための手段】
本発明のある局面に従う前置型非線形歪補償器は、信号変換器の逆特性を用いて、入力信号を変換し、変換後の信号を信号変換器に供給する変換用サポートベクトルマシンと、信号変換器で変換された変換出力信号を受け、変換出力信号列により構成される信号ベクトルと、過去に抽出された変換出力信号列により構成される信号ベクトルとに基づいて、変換用サポートベクトルマシンにおける変換後の入力信号を、第1の不感帯を有する損失関数に基づいて推定する推定用サポートベクトルマシンと、変換用サポートベクトルマシンおよび推定用サポートベクトルマシンに接続され、変換用サポートベクトルマシンの出力および推定用サポートベクトルマシンの出力に基づいて、変換用サポートベクトルマシンおよび推定用サポートベクトルマシンの係数を更新するための係数更新手段と、入力信号としきい値とを比較し、入力信号がしきい値よりも大きい場合、当該入力信号を含むデータセットをサポートベクトルとして採用しないようにするデータ選定手段とを備える。
【0034】
好ましくは、係数更新手段は、変換出力信号を受け、新たに受けた変換出力信号の信号列により構成されるベクトルであって、かつ、第2の不感帯の外にあるベクトルをサポートベクトルの候補として抽出し、既にサポートベクトルとして抽出されているベクトルの集合に加え、前記ベクトルの集合を新たにサポートベクトルの集合とみなし、前記ベクトルの集合の中から、前記第1の不感帯の外にあるベクトルをサポートベクトルとして再抽出する抽出手段と、前記抽出されたサポートベクトルに対する係数を計算する計算手段とを有する。
【0035】
好ましくは、前記しきい値は、所定の定数である。
好ましくは、前記データ選定手段は、過去の所定数の入力信号の絶対値に基づいて、しきい値を設定する。
【0036】
好ましくは、データ選定手段は、所定の期間内の過去の所定数の入力信号の絶対値に基づいて、しきい値を更新する。
【0037】
好ましくは、信号変換器は、増幅器である。
【0038】
【発明の実施の形態】
以下、図面を参照しつつ本発明の実施の形態について詳細に説明する。以下の説明では、同一の構成部分には同一の符号を付してあり、それらの名称および機能も同じである。したがって、それらについての詳細な説明は繰り返さない。
【0039】
[サポートベクトルマシンによる回帰問題の学習の一般論]
以下、本発明の説明を行うにあたり、その前提となるサポートベクトルマシンによる回帰問題の学習について、まとめておく。
【0040】
1−1.線形回帰問題の学習
1−1−1 線形回帰問題
まず、サポートベクトルマシン(SVM)の考えに基づき、サポートベクトル回帰(Support Vector Regression : SVR)の立場から線形回帰問題を解く方法について述べる。この問題は、以下のように定式化できる。
【0041】
[問題]
m入力1出力の未知線形回帰f:x→y があり、トレーニングデータ
(x1,yl),…,(xn,yn) xi∈ Rm, yi∈R (1.1)
が与えられているとする。このとき、トレーニングデータを用いてこの線形回帰を近似する関数
f(x,w)=wTx (1.2)
を求める。
【0042】
1−1−2 損失関数
ここで、線形ε不感損失関数(Linear ε-Insensitive Loss Function)Lε(x,y,f(x,w))ならびに二次ε不感損失関数(Quadtatic ε-Insensitive Loss Function〉L2ε(x,y,f(x,w))を次のように定義する。
【0043】
【数1】
図1は、このような線形ε不感損失関数および二次ε不感損失関数を示す図である。図1(a)は、線形ε不感損失関数であり、図1(b)は、二次ε不感損失関数を示す。
【0044】
1−1−3 二次ε不感損失関数による回帰問題
以下では、二次ε不感損失を用いた場合のサポートベクトル回帰について考える。サポートベクトルマシンに基づいた主問題は、以下のように表現できる。
【0045】
【数2】
この主題は、次のように書き換えることができる。
【0046】
【数3】
ただし、Cはモデルの複雑さと制約条件の緩和(トレーニング誤差)との間のトレードオフを設定する正則化パラメータである。
【0047】
【数4】
式(1.10)に対するKarush-Kuhn-Tucker(KKT)条件により、以下の関係が成り立つ。
【0048】
【数5】
これらの関係式を式(1.10)に代入すると次の双村問題に書き換えられる。
【0049】
【数6】
ここで、係数αiを以下のように置き換えると、式(1.14)は、最終的に以下の式(1.15)のように書き換えることができる。また、式(1.11)により、線形回帰を近似する関数f(x、w)=wTxは、以下の式(1.16)のようになる。
【0050】
【数7】
図2は、線形近似関数とサポートベクトルとの関係を示す概念図である。
【0051】
図2において、「●」がサポートベクトルであり、これらの近似関数による誤差の大きさはεよりも大きい。「○」は近似関数による誤差の大きさがεよりも小さいデータであり、これらは直接近似関数には影響しない。
【0052】
1−2 非線形回帰問題の学習
1−2−1 非線形回帰問題
以上の説明では、サポートベクトル回帰(SVR)を用いた線形回帰について説明した。以下では、それを応用したSVRを用いた非線形回帰について説明する。この非線形回帰問題は、以下のように定式化できる
[問題]
m入力1出力の未知非線形回帰f:x→y があり、トレーニングデータ
(x1,yl),…,(xn,yn) xi∈Rm, yi∈R (1.17)
が与えられているとする。このとき、トレーニングデータを用いてこの非線形回帰を近似する関数f(x,w)=wTxを求める。ここでは、損失関数として、二次ε不感損失関数を用いることにする。
【0053】
1−2−2 特徴空間
一般的に複雑な問題に応用するには、入力空間内で考えるよりも表現能力が優れている空間で考える必要がある。このような手法は高次元化と呼ばれている。
【0054】
ここで、非線形回帰問題に対応するために、入力空間から高次元特徴空間への非線形写像を導入する。入力ベクトルxを入力空間Xから特徴空間Fヘ写像し、その特徴空間でのベクトルφ(x)をこれまでの入力ベクトルxとみなすことにより入力空間ではなく特徴空間で線形回帰問題を取り扱う。ただし、φ:X→Fは、入力空間からある特徴空間への非線形写像である。
【0055】
この作業は、実質的には元の入力空間において非線形回帰問題を解いていることになる。
【0056】
ヒルベルトシュミット理論によるとヒルベルト空間における内積は次のような等価表現ができる。
【0057】
【数8】
以下に示すとおり、特徴空間で線形問題を考えると、式(1.21)となり、また、線形回帰を近似する関数f(φ(x),w)=wTφ(x)は、式(1.22)のようになる。この式(1.22)は、入力空間における線形回帰問題となっており、式(1.20)の関係により、最終的に式(1.23)となる。さらに、式(1.23)をベクトル表記すると、式(1.24)となり、この非線形回帰問題を解くと、式(1.25)の非線形近似関数を得ることができる。
【0058】
【数9】
ここで、注目すべき点は、特徴空間内での内積計算を入力空間内での計算に置き換えることができるカーネル関数K(xi,xj)を用いることにより、双対問題の式(1.21)やそれを解くことによって得られる近似関数にはφ(x)が含まれないので、実際には入力空間から特徴空間への非線形写像を計算する必要はない点である。これは、「カーネルトリック」と呼ばれている。
【0059】
このような特徴があるため、高次元化を導入することにより、サポートベクトル回帰(SVR)では特徴空間の次元を非常に大きくとることもでき、さらにモデルの複雑さと特徴空間の次元とを独立に制御することが可能となる。このことより、SVRはいわゆる次元の呪いから逃れることができる。
【0060】
図3は、非線形近似関数とサポートベクトルを示す概念図である。図3でも、「●」がサポートベクトルであり、これらの近似関数による誤差の大きさはεよりも大きい。「○」は近似関数による誤差の大きさがεよりも小さいデータであり、これらは直接近似関数には影響しない。
【0061】
1−2−3 サポートベクトルと係数の関係
二次ε不感損失関数を用いたSVR問題では、式(1.14)から式(1.15)に係数の置換えを行う前においては、式(1.11)〜(1.13)のKKT条件が成り立っていることから、係数の置換え後においては結局以下の関係式が成り立つ。
【0062】
【数10】
また、二次ε不感損失関数は、不感帯εを有するので、推定誤差の大きさがεよりも小さい、以下の式(1.27)を満たすデータセット(xi,yi)はサポートベクトルから外れる必要がある。このため、得られた解によるサポートベクトルの近似誤差の大きさは、式(1.28)のようになる。
【0063】
【数11】
さらに、ラグランジェ関数を式(1.10)のようにおいたので、以下の式(1.29)および式(1.30)の符号が等しくなる。このため、式(1.23)の解であるサポートベクトルの係数αiは、式(1.31)を満たすことになる。
【0064】
【数12】
2−1 サポートベクトル回帰の学習に対する本発明の方法
以上の説明の方法をそのまま実行しようとすると、SVR問題においてトレーニングデータが多い場合、問題を解くために非常に多くの時間を費やしてしまう。そこで、本発明においては、SVR問題を効率良く解くために、以下に説明するとおり、ニュートン・ラフソン(Newton−Raphson)法を変形させた基本的な更新式を求め、その更新式を用いた逐次形アルゴリズムを採用する。
【0065】
2−1−1 問題設定
ここでは、二次ε不感損失関数を使用する次の問題を解く方法について説明する。
【0066】
[問題]
m入力1出力の未知非線形回帰f:x→y があり、トレーニングデータ
(x1,yl),…,(xn,yn) xi∈Rm, yi∈R
が与えられているとする。このとき、トレーニングデータを用いてこの非線形回帰を近似する式(2.1)の関数を求めるために、式(2.2)で表される最大化問題を解く。
【0067】
【数13】
SVRでは、誤差を評価するときに不感帯を設けているので、この問題を解いて得られたf(x,α)とトレーニングデータには、以下に述べるような関係が成り立っていなければならない。
【0068】
すなわち、データセット(xi,yi)が不感帯の内側にあるならば、つまり、|yi−f(xi,α)|≦εを満たすならば、係数はαi=0となる。
【0069】
逆に、データセット(xi,yi)が不感帯の外側にあるならば、つまり、|yi−f(xi,α)|>εを満たすならば、係数αiは、上述した式(1.31)を満たす。
【0070】
以下に述べるサポートベクトル回帰の学習では、上記の関係を考慮して、不必要となったデータセットをサポートベクトルから除外していく方法をとっている。
【0071】
2−1−2 バッチ処理
以下では、はじめにn個のトレーニングデータからいくつかのデータセットを取り出し、その取り出したデータセットだけを用いてSVRを求める方法について説明する。
【0072】
(ニュートン・ラフソン法の修正)
以下、二次ε不感損失関数に対する双対問題をニュートン・ラフソン法を変形させて更新式を用いて解く方法について説明する。
【0073】
式(2.2)の最大化問題をベクトル表記すると、式(2.3)のようになり、かつ、評価関数W(α)をテイラー展開すると、式(2.4)のようになる。
【0074】
その上で、W(α)をαiの近傍で二次関数近似を行ったとして、上式(2.4)の第3項までで打ち切る。
【0075】
【数14】
この二次関数近似の最小値を与えるα=αiは、以下の式(2.5)の条件により与えられ、そのような最小値を与えるα=αiは、逐次的に以下の式(2.6)の関係を満たすことになる(ニュートン・ラフソン法)。
【0076】
【数15】
(αの更新方法(初期値0の場合))
ニュートン・ラフソン法に基づきαを求める際、初期値α0=0の場合について考える。式(2.6)で、α0=0とすると、以下の式(2.12)および式(2.13)を満たすことになるが、本発明においては、ε=0とおいて、式(2.14)のように修正する。
【0077】
【数16】
その後、さらに式(2.6)を用いて更新すると、以下の式(2.15)および(2.16)のようになる。さらに、αi1≠0のとき、式(2.17)が成り立つので、式(2.16)は、式(2.18)および(2.19)で表されるようになる。
【0078】
【数17】
このように求めた係数ベクトルαで、以下の式(2.20)が成り立っている場合、式(2.21)のようになるので、上述した式(1.31)を満たしていることがわかる。
【0079】
【数18】
しかし、求めた解が式(2.20)を満たしていない場合、その解は式(1.31)を満たしてなく、解としてはふさわしくない。
【0080】
(余分なデータセットの除去方法)
次に、式(2.20)を満たしていない場合について考えることにする。
【0081】
式(2.20)を満たしていない場合は、求めた解は式(1.31)を満たしてなく、KKT条件を満たさないので解ではないことになる。そこで、このような場合は、余分なデータセット(xi,yi)が現在のサポートベクトルの候補の中に存在していると考え、現在のサポートベクトルの侯補の中から余分なデータセットを取り除くことにする。
【0082】
以下では、さらに、余分なデータセットの選出方法について以下に述べる。
まずはじめに、先ほどの更新式を用いて、以下の式(2.22)に基づいて、係数ベクトルαnsvを求める(初期値:0)。
【0083】
次に、係数ベクトルαnsvの各要素はゼロではない(αi≠0,i=1,…,nsv)と考え、さらに更新式(2.6)にステップサイズη(0<η≦1)を導入して、以下の式(2.23)のような新たな更新式をつくる。
【0084】
【数19】
この更新式を用いて係数ベクトルαnsvを更新する際、更新前後で係数ベクトルαnsvの各要素の符号が変化しない範囲で更新を行うことにする。
【0085】
次に、ステップサイズの決め方について説明する。
ステップサイズは、1に近ければ近いほど評価関数が大きな値となるので、できる限り1に近いことが望ましい。そこで、次のようにしてそのステップサイズを求める。
【0086】
まず、以下の式(2.24)により、ステップサイズベクトルを計算する。
【0087】
【数20】
だたし、ステップサイズベクトルη=[η1,…,ηnsv]Tであり、ηiは、更新式(2.23)においてステップサイズη=ηiで、係数ベクトルαnsvを更新するとαi=0となる値である。
【0088】
つぎに、ステップサイズベクトルηの要素の中で、0以上で、かつ、最も小さい要素ηiをステップサイズとして更新を行う。このとき、αi=0であり、データセット(xi,yi)を余分なデータセットであるとし、以下の式(2.25)のようにサポートベクトルから外すことにする。
【0089】
【数21】
これに伴いサポートベクトルの個数が減少することになる(nsv←nsv−1)。
【0090】
サポートベクトルの個数が減少した後、再び更新式(2.23)より係数ベクトルαnsvを更新する。このときも先ほどと同じように、更新前後で係数ベクトルαnsvの各要素の符号が変化しない範囲で更新を行うために式(2.24)からステップサイズηを求める。
【0091】
ステップサイズベクトルηの要素の中で0以上で最も小さい要素ηiが1以上の場合、更新式(2.23)においてη=1で更新した係数ベクトルαnsvは更新前後で各要素の符号が変化しないことがわかる。
【0092】
このとき、係数ベクトルαnsvが決定する。逆にステップサイズベクトルηの要素の中で0以上で最も小さい要素ηiが1よりも小さい場合、先ほどと同じく更新式(2.23)においてステップサイズη=ηiで係数ベクトルαnsvを更新し、データセット(xi,yi)をサポートベクトルから外すことにする。以降、係数ベクトルαnsvが決定するまでこの作業を繰り返し行う。
【0093】
2−1−3 逐次処理
以上の説明では、n個のトレーニングデータからいくつかのデータセットを取り出し、その取り出したデータセットだけからSVRを求める方法について説明した。しかし、バッチ処理では逆行列の計算を行っているため、扱うデータ数には限界がある。そこで、このような問題を回避するために、次に逐次処理について説明する。
【0094】
ここでは、既に以下の式(2.26)のようなSVRによる近似関数が存在しており、新たなトレーニングデータ(xs,ys)を用いて、このSVRによる近似関数を更新する方法について説明する。
【0095】
【数22】
まず、はじめに、新たなトレーニングデータ(xs,ys)が不感帯の内側にあるかどうかを調べる。
【0096】
もし、以下の式(2.27)が成り立つならば、不感帯の内側にあることになりSVRの更新は必要でないが、新たなトレーニングデータ(xs,ys)が不感帯の外側にある場合、つまり以下の式(2.28)が成り立つ場合、SVRの更新が必要となる。
【0097】
【数23】
そこで、新たなトレーニングデータ(xs,ys)が不感帯の外側にある場合について考えることにする。
【0098】
このとき、(x1,y1),…,(xnsv,ynsv),(xs,ys)をサポートベクトルであるとみなす。
【0099】
先ほど示した式(2.23)を用いて、係数ベクトルαを更新しようとした場合、新たなトレーニングデータ(xs,ys)の係数αsが決まっていないのでこの値の初期値を0とする。
【0100】
しかし、このままでは、式(2.23)を計算する際、sign(αs)=0となり、このまま係数ベクトルαを更新して求めても、KKT条件を満たさない。
【0101】
そこで、更新式(2.23)を次のように変更する。
【0102】
【数24】
この後は、更新式(2.29)を用いてαを更新することを考える。ここでも、更新前後で、係数ベクトルαnsvの各要素の符号が変化しない範囲で更新を行うために式(2.24)を次のように変更し、ステップサイズηを求める。
【0103】
【数25】
これ以降は、バッチ処理のところで行ったようにαの更新を行い、αを決定する。
【0104】
実際には、本発明においては、以下の前置型非線形歪補償システムの処理において説明するとおり、大量のトレーニングデータセットが与えられている場合についてのSVRを求めるアルゴリズムを用いる。
【0105】
このアルゴリズムは、バッチ処理・逐次処理を一つにまとめた計算方法である。
【0106】
[非線型デバイス(NLD)の飽和特性を特に考慮しない構成]
図4は、本発明の前置型非線形歪補償システムの構成を説明するにあたり、その理解の前提として、非線型デバイス(NLD)の飽和特性を特に考慮しない構成を有する前置型非線形歪補償システム1000を示す概略ブロック図である。
【0107】
図4に示した例では、増幅器16の出力の歪を前置型非線形歪補償器により補償する構成となっている。
【0108】
図4を参照して、前置型非線形歪補償システム1000は、無線周波数信号SINを中間周波数信号に変換するダウンコンバータ2と、ダウンコンバータ2に接続され、ダウンコンバータ2の出力する中間周波数信号をサンプリングしてデジタル信号に変換するA/D変換器4と、A/D変換器4に接続され、サンプリングされた中間周波数信号をベースバンド信号x(t)に変換する直交検波器6と、直交検波器6に接続され、信号x(t)を、後述する増幅器16の逆特性を用いて、ベースバンド信号y(t)の実数部Re{y(t)}に変換するSVM54と、直交検波器6に接続され、信号x(t)を、増幅器16の逆特性を用いて、ベースバンド信号y(t)の虚数部Im{y(t)}に変換するSVM58と、SVM54および58に接続され、変換後のベースバンド信号y(t)を中間周波数信号に変換する直交変調器10と、直交変調器10に接続され、直交変調器10の出力する中間周波数信号をアナログ信号に変換するD/A変換器12とを含む。
【0109】
なお、本願発明は、図4において、ダウンコンバータ2、A/D変換器4および直交検波器6からなる受信部1の代わりに、無線送信機のベースバンド信号の出力部が接続されるような態様にも適用可能である。
【0110】
前置型非線形歪補償システム1000は、さらに、D/A変換器12に接続され、アナログの中間周波数信号を無線周波数信号S0に変換し、増幅器16に供給するアップコンバータ14と、増幅器16に接続され、増幅器16より出力される出力信号SOUTを中間周波数信号に変換するダウンコンバータ18と、ダウンコンバータ18に接続され、中間周波数信号をデジタル信号に変換するA/D変換器20と、A/D変換器20に接続され、デジタル信号をベースバンド信号z(t)に変換する直交検波器22とを含む。
【0111】
前置型非線形歪補償システム1000は、さらに、直交検波器22の出力する信号z(t)と学習に用いたベースバンド信号ベクトルV_z(pi)(i=1,…,nR)とに基づいて、SVM54より出力されるベースバンド信号の実数部の推定値Re{y′(t)}を出力するSVM26と、直交検波器22の出力する信号z(t)とベースバンド信号ベクトルV_z(qj)(j=1,…,nI)とに基づいて、SVM58より出力されるベースバンド信号の虚数部の推定値Im{y′(t)}を出力するSVM62と、SVM54およびSVM26に接続され、ベースバンド信号の実数部の推定値Re{y′(t)}とベースバンド信号y(t)の実数部Re{y(t)}との差分を計算する減算器30と、SVM58およびSVM62に接続され、ベースバンド信号の虚数部の推定値Im{y′(t)}とベースバンド信号y(t)の虚数部Im{y(t)}との差分を計算する減算器64と、直交検波部6および直交検波部22に接続され、信号ベクトルおよびサポートベクトルのサイズmと増幅器16による遅延時間dとを求めるm・d決定部44と、減算器30、SVM54、SVM26、直交検波部22およびm・d決定部44に接続され、減算器30の出力、直交検波部22の出力およびm・d決定部44の出力に基づいて、SVM54およびSVM26における、増幅器16の逆特性を有する関数の係数αR(i)を更新する係数更新部42と、減算器64、SVM58、SVM62、直交検波部22の出力およびm・d決定部44に接続され、減算器64の出力、直交検波部22の出力およびm・d決定部44の出力に基づいて、SVM58およびSVN62における、増幅器16の逆特性を有する関数の係数αI(j)を更新する係数更新部66とを含む。
【0112】
SVM26は、後に説明する方法に従い、ベースバンド信号の実数部の推定値Re{y′(t)}を求める。SVM62は、SVM26と同様の方法に従い、ベースバンド信号の虚数部の推定値Im{y′(t)}を求める。
【0113】
係数更新部42は、Re{y(t)}とRe{y′(t)}との誤差eR(t)が最小になるように係数αR(i)を制御する。係数更新部66は、係数更新部42と同様に、Im{y(t)}とIm{y′(t)}との誤差eI(t)が最小になるようにαI(j)を制御する。
【0114】
なお、直交検波器6をアナログで実現し、ダウンコンバータ2の出力を直交検波器6で受け、直交検波器6の出力をA/D変換器4でデジタルに変換し、その出力をSVM8に供給する構成であっても構わない。また、直交変調器10をアナログで実現し、SVM54およびSVM58の出力をD/A変換器12が受け、D/A変換器12の出力を直交変調器10で受け、直交変調器10の出力をアップコンバータ12に供給する構成であっても構わない。さらに、直交検波器22をアナログで実現し、ダウンコンバータ18の出力を直交検波器22で受け、直交検波器22の出力をA/D変換器20で受け、A/D変換器20の出力をSVM26およびSVM62に供給する構成であっても構わない。
【0115】
(前置型非線形歪補償システム1000の動作)
以下、前置型非線形歪補償システム1000の動作について説明する。
【0116】
まず、図4において、信号SIN、S0およびSOUTは、式(1)〜(3)でそれぞれ表わされる。
【0117】
SIN=Re{x(t)exp(j2π(fRFt)}
:前置型非線形歪補償器への入力信号 …(1)
S0=Re{y(t)exp(j2π(fRFt)}
:歪補償された信号 …(2)
SOUT=Re{z(t)exp(j2π(fRFt)}
:増幅器16からの出力信号 …(3)
x(t)、y(t)およびz(t)は、それぞれ帯域信号SIN、S0およびSOUTの複素包絡線 (ベースバンド信号)である。jは虚数を表わす。fRFは無線周波数(Radio Frequency)を表わす。tは時刻を表わす。
【0118】
[非線形歪補償器の動作原理]
P=|y(t)|2/2として、増幅器16のベースバンド領域における入出力特性をfを複素関数としてf(P)と置くと、ベースバンド信号y(t)およびz(t)の関係は、下記の式(4)のように表すことができる。
【0119】
さらに、一般に、非線形歪補償器では、f(P)に対し、次式(5)の関係を満たす入出力特性g(P)を求めることを目的とする。仮に、入出力特性g(P)を得ることができれば、次式(6)および(7)が成立ち、SINに対してSOUTを線形化することができる。
【0120】
【数26】
前置型非線形歪補償システム1000では、g(P)を、SVM26および係数更新部42ならびにSVM62および係数更新部66にて推定する。具体的には、y(t)とz(t)より推定したy′(t)との誤差e(t)が、実部および虚部のそれぞれにおいて最小になるように、SVM26およびSVM62の関数の係数を更新する。この計算が収束すれば、SVM26およびSVM62により近似される特性は、増幅器16の逆特性に相当することとなる。
【0121】
[逆特性関数の計算]
上述したような逆特性関数の計算のための条件を以下に整理しておく。
・非線形の歪補償のための計算は時間連続信号ではなく離散信号に対して行なわれる。ハードウェア化の際は、A/D変換器を使用し、連続信号を離散信号に変換し、計算後、離散信号を連続信号にD/A変換器により復元する。
・信号処理は帯域系ではなくベースバンド系または中間周波数信号にて行なわれる。ベースバンド系の場合には、増幅器16は等価的に複素ベースバンド信号y(t)を受け、複素信号z(t)を出力する系と見なすことができる。
【0122】
[サポートベクトルマシンの動作説明]
時刻kT(T:A/D変換およびD/A変換のサンプリング間隔)のとき、サポートベクトルマシンSVM54の出力Re{y(kT)}およびSVM58の出力Im{y(kT)}、ならびにサポートベクトルマシンSVM26の出力Re{y′s(kT)}およびSVM62の出力Im{y′s(kT)}は、次式(8)〜(11)により得られる。
【0123】
【数27】
ここで、変数の接頭辞”V_”は、その変数がベクトルであることを表わす。また、mは信号ベクトルおよび後述するサポートベクトルのサイズ、nR、nIは、それぞれ実部および虚部のサポートベクトルマシンのサポートベクトルの数であり、piはi番目のサポートベクトルを取得した時間であり、qjはj番目のサポートベクトルを取得した時間である。
【0124】
V_z(piT)(i=1,…,nR),V_z(qjT)(j=1,…,nI)
は増幅器16の入出力特性を学習した結果、時刻kTまでに抽出されたサポートベクトルである。
【0125】
αR(i),αI(j)は、それぞれV_z(piT),V_z(qjT)に対応した重み係数(実数)である。一般に、αR(i)(または、αI(j))が零の時、対応するV_z(piT)(または、V_z(qjT))は計算に加える必要がなく廃却しても構わない。また、非零の係数αR(i)(または、αI(j))の個数をサポートベクトルマシンの次元と呼ぶ。例えば、非零の係数の個数が73であればサポートベクトルマシンの次元数は73である。さらに、この次元数は学習データを増やしても一定値以上に増えることがない。この上界値のことをVC(Vapnik and Chervonenkis)次元と呼ぶ。
【0126】
K(V_x,V_y)は「内積カーネル」の関数であり、前置型非線形歪補償システム1000では、内積カーネルの線形和である式(8)〜(11)を、適切な係数αR(i),αI(j)を選択することにより、増幅器16の入出力特性の逆特性g(P)に適合させることを目標とする。このように未知の関数にシステムの入出力関数を適合させるような問題全般を総称して「回帰問題」という。次式(15)〜(17)は、一般的に用いられる内積カーネルの例である。
【0127】
【数28】
どの内積カーネルが逆関数を表現するのに最も適しているかはシステムにより異なり、実際には動作前に何度か試験をした上で最も特性のよいものを選択する。もちろん、上記以外の関数でも逆関数g(P)をよりよく推定でき、かつ期待する効果が得られるのであれば、その関数を使用してもよい。
【0128】
[係数更新部42の動作説明]
以下では、サポートベクトルに対応する係数αR(i),αI(j)の更新計算を行う係数更新部42および係数更新部66の動作について説明する。
【0129】
上述したとおり、係数更新部42は、Re{y(t)}とRe{y′(t)}との誤差eR(t)が最小になるように係数αR(i)を制御する。一方、係数更新部66は、Im{y(t)}とIm{y′(t)}との誤差eI(t)が最小になるように係数αI(j)を制御する。
【0130】
【数29】
なお、以下では、表記を簡単にするためT=1としている。このようにしても一般性を失うことはない。
【0131】
係数αR(i)は、次式(20)で表わされる評価関数Wを最大化するという最適化問題を解くことにより得られる。また、係数αI(j)についても同様である。
【0132】
【数30】
ただし、定数Cと定数εは、通常、実験的に求められる。
【0133】
増幅器16の入出力特性の学習が完了するまでの間はサポートベクトルの追加・削除が繰返されるが、これと対応して係数αR(i),αI(j)の値を更新する必要がある。
【0134】
以下では、係数更新部42の動作を例にとって説明する。係数更新部66の動作も、入力される変数が異なるのみで、基本的に係数更新部42と同様である。
【0135】
なお、後に詳しく説明するように、係数更新部42の更新の計算の特徴の1つは、以下のようにして逐次的に係数αR(i)の値を更新することである。
(1) 更新の計算の途中において、係数更新部42は、n−1組のサポートベクトルV_z(pi)および係数αR(i)を取得している状態となる。
(2) 係数更新部42は、さらに、n個目のサポートベクトルの候補としてデータV_z(pn)を入手する。
(3) V_z(pn)をサポートベクトルと見なし、その係数をαR(n)=0とおく。
(4) V_z(pn)が加わったことによる最適解からのずれ(摂動)を補正するため、αR(i)(i=1,…,n)に関して誤差分(摂動分)ΔαR(i)を計算する。
【0136】
上述のように逐次サポートベクトルを抽出することにより、1回の係数更新において計算対象となる係数の数を削減できるので、計算量を削減することができる。
【0137】
[係数の更新の具体的な計算方法]
係数の更新方法の具体例を以下に示す。ただし、この具体例は実現の一例であって、必ずしもこの通りである必要はない。
【0138】
図5および図6は、このような係数の更新の具体的な計算方法を説明するためのフローチャートである。
【0139】
図5を参照して、係数更新部42は、まず、取得済みのN個の学習データセットからn個のデータセット(V_z(Pi),Re{ys(Pi)})(i=1〜n)を取り出し、これらをサポートベクトルに採用する(ステップ100)。
【0140】
次に、係数更新部42は、上記サポートベクトルに対応する係数の第1次近似と、その符号ベクトルSRを、以下の式(21)および(22)により計算する(ステップ102)。
【0141】
【数31】
さらに、ステップサイズベクトル[ηR(1),…,ηR(n)]Tを以下の式(24)および(25)により計算する(ステップS104)。
【0142】
【数32】
ステップサイズベクトルの要素の中で0以上でもっとも小さい要素をηR(ν)とし(ステップS106)、要素ηR(ν)が1以上であるか否かを判定する(ステップS108)。
【0143】
まず、要素ηR(ν)が1未満である場合、続いて、要素ηR(ν)を用いて、以下の式(26)により、係数ベクトル[αR(1),…,αR(n)]Tを更新する(ステップS110)。
【0144】
【数33】
その上で、(V_z(Pν),Re{ys(Pν)})を余分なデータセットとして、サポートベクトルから削除し、係数αR(Pν)も削除する(ステップS112)。このような削除に対応して、i>νについて、以下の表にしたがって、i番目の学習データを取得した時間、および係数αR(i)の番号を読替える。
【0145】
【表1】
さらに、(n−1)を新たにnと読替える処理を行う(ステップS114)。以上の読替えの手続きの後、処理はステップS104に復帰する。
【0146】
一方、ステップS108において、要素ηR(ν)が1以上である場合、以下の式(27)により、改めて係数ベクトルを計算する(ステップS116)。
【0147】
【数34】
次に、図6を参照して、新しい学習データセット(V_z(k),Re{ys(k)})の取得が行われる(ステップS118)。
【0148】
さらに、以下の式(28)により、誤差eRが計算される(ステップ120)。続いて、誤差eRとしきい値ε´との比較が行われて(ステップS122)、|eR|<ε´であれば、処理は、ステップS118に復帰する。なお、ここで、ε≦ε´である。
【0149】
【数35】
一方、|eR|≧ε´であれば、以下の式(29)〜(30)にしたがって、係数αR(1),…,αR(n),および誤差eRのそれぞれについて、符号を計算し、符号ベクトルを置き換え(ステップS124)、[αR(1),…,αR(n),0]を新たに係数ベクトルに置き換えるとともに、(n+1)を新たにnと置き換える(ステップS126)。
【0150】
【数36】
(V_z(k),Re{ys(k)})をn番目のサポートベクトル(V_z(Pn),Re{ys(Pn)})として採用して、処理はステップS104に復帰する(ステップS128)。
【0151】
以上の処理により、係数更新部42は、逐次適応的に係数ベクトルの更新を行う。
【0152】
[サポートベクトルマシンSVM54,58の動作説明]
SVM54は、係数更新部42で更新された係数αR(i)を用いて、上述した式(8)に従い、ベースバンド信号x(t)をベースバンド信号Re{y(t)}に変換する。サポートベクトルマシンSVM58は、上述したのと同様の手続きで、係数更新部66で更新された係数αI(i)を用いて、上述した式(9)に従い、ベースバンド信号x(t)をベースバンド信号Im{y(t)}に変換する。
【0153】
[逐次計算における特徴的手続きの説明]
以上、図5および図6により、サポートベクトルマシンを用いて、非線形なプロセスであって、当該プロセスを表現する変数が複素数で表される場合に、回帰問題を解くことにより、前置型非線形歪補償システムを実現するための構成について説明した。特に、上記係数更新部42の行う処理において、特徴的な手続きについて、以下に説明を付け加えておく。
【0154】
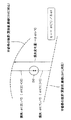
図7は、1入力1出力の非線形回帰f:x→yに関して、サポートベクトルマシンによる近似学習がある程度進んだ状態において、サポートベクトルによる学習データの近似特性を示す概念図である。
【0155】
図7においては、「損失」は、ε不感2次損失関数に基づく近似特性を表しているものとする。つまり、「損失」は、不感帯の片側幅を近似特性に加減して得られた2つの不感帯境界値のうち、学習データに近い方の不感帯境界値を減算することにより得られる値と定義する。
【0156】
図7で、2重丸はサポートベクトルであるデータを表しており、1重丸は、サポートベクトルによる近似特性に対する不感帯の内側に存在し、サポートベクトルではないデータを表す。なお、サポートベクトルの定義により、図7中で2重丸で表されるデータが真のサポートベクトルであるときは、この真のサポートベクトルの外側には、サポートベクトルは存在しない。
【0157】
ここで、たとえば、サポートベクトルによる近似特性の上側であって、かつ、不感帯の外側にあるサポートベクトルのデータD1=(x1,y1)について見てみると、このデータD1についての損失L1は、以下の式で表される。
【0158】
L1=α1/C
なお、ここで、α1はサポートベクトルx1に対する係数である。このとき、データD1の損失は、このデータがサポートベクトルによる近似特性の上側にあることに対応して、「上向き、かつ、外向き」であり、α1>0である。
【0159】
一方、たとえば、サポートベクトルによる近似特性の下側であって、かつ、
不感帯の外側にあるサポートベクトルのデータD2=(x2,y2)について見てみると、このデータD2についての損失L2も、L2=α2/Cで表される。
【0160】
このとき、データD2の損失は、このデータがサポートベクトルによる近似特性の下側にあることに対応して、「下向き、かつ、外向き」であり、α2<0である。
【0161】
(ステップS122におけるε´の値の設定)
ε´の値は、本来の不感帯を定義する値εと同じ値としても計算を実行することは可能である。しかし、本願発明では、ε´の値を本来の不感帯を定義する値εよりも大きくしている。
【0162】
そこで、以上の準備のもとに、まず、図6のステップS122において、ε´の値を本来の不感帯を定義する値εよりも大きくする理由について、まず、説明する。
【0163】
図8は、このようにε´の値を本来の不感帯を定義する値εよりも大きくすることの効果を説明するための概念図である。
【0164】
なお、εで決まる本来の不感帯に対し、εをステップS122のε´で置換えた場合に、ε´で決まる領域を本来の不感帯に対する「拡張不感帯」と定義する。
【0165】
拡張不感帯はステップS122のみにおいて用いられ、他のステップにおける不感帯は、εで決定される。
【0166】
図8においては、学習途中のサポートベクトルによる近似特性が直線LSVで表され、この近似特性よりもさらに近似が進んだ状態の近似特性が曲線CSVで表されているものとする。ただし、「学習途中のサポートベクトルによる近似特性」を直線としたのは、説明の便宜のためであって、より一般には、この特性も曲線で表される。
【0167】
まず、近似特性LSVについて、拡張不感帯をしきい値ε´(=ε)で定義した場合は、データD3は、最終的にはサポートベクトルにはならないデータであるものの、近似特性LSVの段階では、サポートベクトルとして選択されることになる。これは、拡張不感帯を定義するしきい値を、しきい値εよりも大きなしきい値ε´(1)で定義した場合も同様である。
【0168】
これに対して、近似特性LSVについて、拡張不感帯をしきい値ε´(1)よりもさらに大きなしきい値ε´(2)で定義した場合は、データD3は、近似特性LSVの段階でも、サポートベクトルとして選択されない。
【0169】
上述したとおり、本発明においては、計算量を低減するために、逐次計算の途中において、サポートベクトルとして選択されなくなったデータを計算の対象から除外している。
【0170】
したがって、図6のステップS122において使用するしきい値ε´を、予め本来の不感帯に対応するしきい値εよりも大きなしきい値ε´としておけば、計算が進むにつれて、除外されていくはずのデータをそもそもサポートベクトルとして選択する確率が小さくなるので、一層の計算量の低減を期待できる。
【0171】
すなわち、1度、サポートベクトルとして抽出した古いデータセットが、学習(新しいサポートベクトルの追加)が進むにつれ、サポートベクトルとして不要となり除去されることが繰り返され、最終的には新しいサポートベクトルの追加が不要となって学習が終了することになる。しかしながら、「サポートベクトルの追加・除去の繰り返し」を低減することにより、計算量を削減するとともに学習の終了までの時間を短縮することが可能となる。
【0172】
なお、新しいサポートベクトルの追加の頻度が低下するにつれてしきい値ε´(≧ε)をεに近づけていくという処理を行うことも可能である。この場合、ある程度の近似精度までは早期に学習することになり、かつ、最終的な精度εも確実に得ることが可能となる。
【0173】
また、係数更新部42や係数更新部66において、直交検波器22から受取る学習データの数をカウントするカウンタを備えて、一定数のデータを受取るごとにしきい値ε´を更新しつつ、εに近づけていくという処理を行うことも可能である。
【0174】
あるいは、係数更新部42や係数更新部66において、時間を計測するカウンタまたは抽出されたサポートベクトルの数をカウントするカウンタを有し、処理期間の長さに対応して、しきい値ε´を更新しつつ、εに近づけていくという処理を行うことも可能である。
【0175】
(サポートベクトルを削除する基準)
さらに、図5のステップS110からS114において、サポートベクトルを削除する基準について、さらに説明する。
【0176】
図9は、図8で示される状態から、近似特性の逐次計算を進めた場合に、余分となったサポートベクトルの除去を行う手続きを説明するための概念図である。
【0177】
以下の説明では、図8で示される状態で、しきい値εと近似特性LSVにより決まる不感帯の外にデータD3があるため、データD3がサポートベクトルとして選択されており、図9に示す状態に近似を進めると、このデータD3がサポートベクトルから除去され、一方、データD1が新たにサポートベクトルとして追加されるものとする。
【0178】
図10は、図9において、データD3について、損失の変化を説明するための概念図である。
【0179】
なお、ここでは、直線LSVで表される近似特性で、このデータD3に対応する係数をαi(1)とし、曲線CSVで表される近似特性でのデータD3に対応する係数をαi(2)と表すものとする。
【0180】
直線LSVの不感帯の境界の外側にデータD3が存在することに対応して、直線LSVに対するデータD3の損失は、αi(1)/C(αi(1)>0)となる。
【0181】
これに対して、曲線CSVの不感帯の境界の内側にデータD3が存在することに対応して、曲線CSVに対するデータD3の損失は、αi(2)/C(αi(2)<0)となる。
【0182】
したがって、近似が進んで、サポートベクトルによる近似特性が、直線LSV(より一般的には曲線)から、曲線CSVへと変化することによる損失の変化量を、−Δαi/Cとすると、ステップS108で用いたステップサイズηは、η=−αi(1)/Δαiと表される。
【0183】
このとき、0≦η<1が成り立っていれば、図10で示すように、直線LSV(より一般的には曲線)の不感帯の境界と曲線CSVの不感帯の境界との間にデータD3が存在することになる。これは、言い換えると、「データD3は、サポートベクトルによる近似特性が、直線LSV(より一般的には曲線)から、曲線CSVと変化することにより、サポートベクトルから除去されるデータとなった」ということができる。なお、以上の説明では、データが近似特性の上側にある場合について説明したが、データが近似特性の下側にある場合にも同様である。
【0184】
したがって、図5のステップS108におけるような基準で判断することにより、それまでサポートベクトルとして選択していたデータをサポートベクトルから除外するべきか否かを判断することが可能となる。
【0185】
上述の例では、入出力特性が不明な、非線形の入出力特性を有する増幅器16の出力の補正に対して、サポートベクトルマシンを用いたが、本発明は増幅器16に対してのみ適用可能なわけではない。一般的に、入力される信号が複素数で表現でき、かつ入出力特性が不明な信号の変換回路に対しても本発明を適用することが可能である。
【0186】
以上説明したように、前置型非線形歪補償システム1000によると、SVM26およびSVM62を用いて、増幅器16の逆特性を有する信号を推定する。その信号とSVM54およびSVM58より出力される信号とに基づいて、係数更新部42および係数更新部66において、増幅器16の逆特性を有する関数の係数が更新される。
【0187】
この構成では、ルックアップテーブルを必要としないため、ノイズフロアを低く押さえることができ、かつ、入力が複素信号である場合に適用可能であるので、簡単な構成で前置型非線形歪補償器を提供することができる。また、サポートベクトルマシンは、pth−order−predistorterに比べて、計算が簡単で収束時間が早い。さらに、学習する過程で、一度、サポートベクトルに加えられた信号ベクトルにおいて、不要となったサポートベクトルが削除されるため、高速処理が可能な前置型非線形歪補償器を提供することができる。
【0188】
また、広帯域信号が入力された場合、増幅器の非線形性が信号帯域に比較して狭帯域の場合にもデータベクトルのサイズmを適切に設定することにより補償することが可能である。
【0189】
[本発明の実施の形態の前置型非線形歪補償システム2000]
以上、図4に示した前置型非線形歪補償システム1000の構成および動作について説明した。
【0190】
前置型非線形歪補償システム1000は、上述のような特徴を有するものの、図20に示したような入出力特性を有する増幅器において、バックオフを小さく取ると以下のような問題がある。
【0191】
すなわち、増幅器への入力が大きい場合、増幅器の飽和特性により、出力はある値に抑えられる。その飽和した出力が推定用SVM26および62の入力となるので、推定用SVM26および62の出力は変換用SVM54および58の出力に比べて小さくなる。
【0192】
したがって、推定用SVM26および62の出力と変換用SVM54および58の出力との差分は、入力信号が小さいときには非常に小さな値となるが、入力が大きいときは非線形歪の影響を受け大きくなる。
【0193】
図4に示した前置型非線形歪補償システム1000の方式では、各トレーニングデータについて、両SVM出力の差分が予め設定した不感帯ε′よりも大きいとき、サポートベクトルとして採用する。過剰に大きな振幅のトレーニングデータにおける両SVM出力の差分は、確実に不感帯ε′よりも大きくなり、サポートベクトルとして採用される。このため、このトレーニングデータにより全てのサポートベクトルは更新され、回帰関数の近似精度は悪くなる。このようなトレーニングデータが複数個採用されることにより、回帰関数の精度はますます悪くなり、場合によっては発散してしまう。
【0194】
図11は、本発明の前置型非線形歪補償システム2000の構成を説明するための概略ブロック図である。
【0195】
図4に示した前置型非線形歪補償システム1000に比べて、前置型非線形歪補償システム2000には、データ選定部70がさらに設けられている。前置型非線形歪補償システム2000のその他の構成は、前置型非線形歪補償システム1000と同様であるので、同一部分には同一符号を付して、その説明は繰り返さない。
【0196】
なお、図11において、非線形デバイス16は、たとえば、図20に示したような入出力特性を有する増幅器であるものとする。
【0197】
図11を参照して、データ選定部70は、入力されるベースバンド信号x(t)と、後に説明するしきい値THとを比較し、信号x(t)がしきい値よりも大きい場合、その信号x(t)を含むデータセットをサポートベクトルとして採用しないようにするものである。
【0198】
図12は、データ選定部70の構成を説明するための概略ブロック図である。
図12を参照して、データ選定部70は、ベースバンド信号x(t)を伝達する経路を選択するための選択部702と、少なくとも指定された個数のNTH個のベースバンド信号x(t)を選択部702から受けて格納するためメモリ704と、メモリ704中に格納されたベースバンド信号x(t)からしきい値THを算出するためのしきい値決定部706と、選択部702からのベースバンド信号x(t)としきい値THとを比較して、しきい値TH以下のベースバンド信号x(t)を選択的に係数更新部42および66に与えるための比較部708とを備える。
【0199】
ここで、しきい値決定部706は、以下の式に基づいて、しきい値THを算出する。
【0200】
【数37】
ここで、上式において、K1およびNTHは、予め指定される定数である。
【0201】
なお、しきい値THを計算するためのベースバンド信号x(t)は、たとえば、一定の時間間隔ごとに少なくとも個数NTHがメモリ704に格納されて、しきい値決定部706が、この一定時間間隔ごとにしきい値THを更新することとしてもよい。
【0202】
また、しきい値THの決定の仕方は、上述した方法に限られず、たとえば、所定の定数としてもよいし、あるいは、以下の式のように、過去のベースバンド信号x(t)の絶対値の最大値に所定の定数K2を乗算することで、更新することとしてもよい。
【0203】
【数38】
すなわち、データ選定部70においてベースバンド信号x(t)を選択するためのしきい値THは、外部から任意に設定可能である。または、データ選定部70におけるしきい値THは、過去の入力信号から、所定の計算により設定もしくは更新することが可能である。
【0204】
次に、図11に示した前置型非線形歪補償システム2000について説明する。ただし、その動作は、基本的に、図5および図6で説明した前置型非線形歪補償システム1000の動作と同様であるので、以下では、主として、前置型非線形歪補償システム2000の動作の前置型非線形歪補償システム1000の動作との相違点について説明する。
【0205】
図13および図14は、前置型非線形歪補償システム2000の係数更新の動作を説明するためのフローチャートである。
【0206】
まず、図13を参照して、サポートベクトル係数の第1次近似を行うため、データセットをNセット取得する。その際、対応するベースバンド信号x(t)も併せて取得しておく(ステップS200)。
【0207】
次に、データ選定部70において、しきい値THを決定する(ステップS201)。ここでは、たとえば、上述したうち、個数NTHのベースバンド信号x(t)の絶対値の平均値に係数K1を乗じて得られるものとする。
【0208】
次に、各データセットについてベースバンド信号x(t)としきい値THとを比較し、入力信号がしきい値THよりも大きい場合は、そのデータを含むデータセットは回帰関数の精度を悪くするデータセットであるとみなし、サポートベクトルに採用しない(ステップS202)。
【0209】
残りのデータセットの数をnとすると、データセットは、(V_z(Pi),Re{ys(Pi)})(i=1〜n)である。係数更新部42は、上記サポートベクトルに対応する係数の第1次近似と、その符号ベクトルSRを、図5におけるステップS102と同様にして計算する(ステップ203)。
【0210】
以下、図5のステップS104〜S116と同様の処理を、図13においても、ステップS204〜S216として実行する。
【0211】
次に、図14を参照して、新しい学習データセット(V_z(k),Re{ys(k)})の取得が行われる(ステップS218)。併せて、対応する入力信号のベースバンド信号x(t)も取得する。
【0212】
そのときの入力信号のベースバンド信号x(t)がしきい値TH以上である場合(ステップS219)、そのデータセットをサポートベクトルに採用しないで、処理は、ステップS218に復帰する。
【0213】
一方、ステップS219において、入力信号のベースバンド信号x(t)がしきい値THよりも小さい場合は、さらに、上述した式(28)により、誤差eRが計算される(ステップ220)。
以下、図6におけるステップS122〜128と同様の処理が、図14においても、ステップS222〜S228として実行される。
【0214】
以上の処理により、係数更新部42は、逐次適応的に係数ベクトルの更新を行う。
【0215】
SVM54は、係数更新部42で更新された係数αR(i)を用いて、上述した式(8)に従い、ベースバンド信号x(t)をベースバンド信号Re{y(t)}に変換する。サポートベクトルマシンSVM58は、上述したのと同様の手続きで、係数更新部66で更新された係数αI(i)を用いて、上述した式(9)に従い、ベースバンド信号x(t)をベースバンド信号Im{y(t)}に変換する。
【0216】
[シミュレーション結果]
以下、本発明の効果を示すために、シミュレーション結果を示す。
【0217】
以下のシミュレーションでも、NLDは増幅器とし、その入出力特性は次式で表されるものとする。
【0218】
【数39】
その他の条件として、入力信号はOFDM信号とし、そのキャリア数は1405であり、FFTサイズは2048であるものとする。
【0219】
信号電力対雑音電力比(以下、「SNR」という)は、100(dB)である。入力電力は1とし、しきい値THは固定で0.8としている。
【0220】
データセット数は2000である。また、m=1とする。さらに、dは既知であるものとする。
【0221】
図15は、入力信号をバックオフ6(dB)で、増幅器16に通した後の信号スペクトラムである。すなわち、図15においては、前置型非線形歪補償システムを設けることなく、増幅器16で、入力信号を増幅した場合の特性のシミュレーション結果を示している。
【0222】
図15において、横軸は周波数キャリア番号、縦軸は電力を表している。非線形歪の影響を受けて、SNRは、約20(dB)にまで悪化している。
【0223】
さらに、図16は、このような状況において、データ選定部70が設けられていない前置型非線形歪補償システム1000による信号スペクトラムを示す。
【0224】
増幅器16のみの場合よりも信号帯域外のスペクトラムが上昇しており、逆にSNRは小さくなってしまう。これは、過剰に大きな信号を要素にもつデータセットがサポートベクトルとして採用されてしまったからである。そのデータセットにより回帰関数は、もはや増幅器の逆特性を正確に近似できるものではなくなっている。そのデータセット以降のデータセットは、すべてサポートベクトルとして採用されることになり、サポートベクトル数が多くなる。併せて、サポートベクトル係数は極端に大きな数字となり、やがて発散する。
【0225】
図17は、図16の状態におけるサポートベクトル係数を表す図である。図17において、横軸はサポートベクトル番号、縦軸はサポートベクトル係数値である。このとき、サポートベクトル数は約1450個と非常に多く、それに伴って計算量も莫大なものになっている。
【0226】
図18は、データ選定部70を搭載した本発明の前置型非線形歪補償システム2000による信号スペクトラムを示す図である。増幅器16のみの場合よりも信号帯域外のスペクトラムが下降しており、SNRは約30(dB)に改善された。これは、発散を招く原因となる過剰に大きな信号を要素にもつデータセットをサポートベクトルに採用しなかったことが理由であると考えられる。
【0227】
したがって、バックオフが小さい場合でも、本発明による方式により非線形歪の影響を小さくすることができる。
【0228】
図19は、図18におけるサポートベクトル係数を表す図である。サポートベクトル数は71個となっており、前置型非線形歪補償システム1000と比較して大幅にサポートベクトル数が減少していることが確認できる。併せて、カーネル行列の大きさが小さくなったことにより、計算量も格段に減少している。
【0229】
今回開示された実施の形態はすべての点で例示であって制限的なものではないと考えられるべきである。本発明の範囲は上記した説明ではなくて特許請求の範囲によって示され、特許請求の範囲と均等の意味および範囲内でのすべての変更が含まれることが意図される。
【0230】
【発明の効果】
以上説明したとおり、本発明によれば、サポートベクトルマシンを用いて、増幅器等の信号の変換回路の逆特性を有する信号を推定するので、ルックアップテーブルを必要としないため、ノイズフロアを低く押さえることができる。
【0231】
しかも、入力が複素信号である場合に適用可能であるので、簡単な構成で前置型非線形歪補償器を提供することも可能となる。
【0232】
さらに、学習する過程で、一度、サポートベクトルに加えられた信号ベクトルにおいて、不要となったサポートベクトルが削除されるため、高速処理が可能である。
【0233】
また、本発明により、SVRのみを用いた前置型非線形歪補償器歪においては、補償できない過剰に大きな信号をトレーニング用のデータセットから削除するので、回帰関数の精度を維持することができる。
【0234】
さらに、本発明により、データセットを削除したことにより計算が安定し、同時にサポートベクトル数を少なくすることができるため、計算量を大幅に削減することが可能となる。
【図面の簡単な説明】
【図1】 線形ε不感損失関数および二次ε不感損失関数を示す図である。
【図2】 線形近似関数とサポートベクトルとの関係を示す概念図である。
【図3】 非線形近似関数とサポートベクトルを示す概念図である。
【図4】 本発明の前置型非線形歪補償システム1000の構成を説明するための概略ブロック図である。
【図5】 係数の更新の具体的な計算方法を説明するための第1のフローチャートである。
【図6】 係数の更新の具体的な計算方法を説明するための第2のフローチャートである。
【図7】 サポートベクトルマシンによる近似学習がある程度進んだ状態において、サポートベクトルによる学習データの近似特性を示す概念図である。
【図8】 ε´の値を本来の不感帯を定義する値εよりも大きくすることの効果を説明するための概念図である。
【図9】 近似特性の逐次計算を進めた場合に、余分となったサポートベクトルの除去を行う手続きを説明するための概念図である。
【図10】 図9において、データD3について、損失の変化を説明するための概念図である。
【図11】 本発明の前置型非線形歪補償システム2000の構成を説明するための概略ブロック図である。
【図12】 データ選定部70の構成を説明するための概略ブロック図である。
【図13】 前置型非線形歪補償システム2000の係数更新の動作を説明するための第1のフローチャートである。
【図14】 前置型非線形歪補償システム2000の係数更新の動作を説明するための第2のフローチャートである。
【図15】 入力信号をバックオフ6(dB)で、増幅器16に通した後の信号スペクトラムである。
【図16】 データ選定部70が設けられていない前置型非線形歪補償システム1000による信号スペクトラムを示す。
【図17】 図16の状態におけるサポートベクトル係数を表す図である。
【図18】 データ選定部70を搭載した本発明の前置型非線形歪補償システム2000による信号スペクトラムを示す図である。
【図19】 図18におけるサポートベクトル係数を表す図である。
【図20】 一般な増幅器の入出力特性を示す図である。
【符号の説明】
2,18 ダウンコンバータ、4,20 A/D変換器、6,22 直交検波器、54,58,26,62 SVM、10 直交変調器、12 D/A変換器、14 アップコンバータ、16 増幅器、30,64 減算器、42,66 係数更新部、70 データ選定部、1000,2000 前置型非線形歪補償システム。
Claims (4)
- 信号変換器の逆特性を用いて、入力信号を変換し、変換後の信号を信号変換器に供給する変換用サポートベクトルマシンと、
前記信号変換器で変換された変換出力信号を受け、前記変換出力信号列により構成される信号ベクトルと、過去に抽出された変換出力信号列により構成される信号ベクトルとに基づいて、前記変換用サポートベクトルマシンにおける変換後の入力信号を、第1の不感帯を有する損失関数に基づいて推定する推定用サポートベクトルマシンと、
前記変換用サポートベクトルマシンおよび前記推定用サポートベクトルマシンに接続され、前記変換用サポートベクトルマシンの出力および前記推定用サポートベクトルマシンの出力に基づいて、前記変換用サポートベクトルマシンおよび前記推定用サポートベクトルマシンの係数を更新するための係数更新手段と、
前記入力信号としきい値とを比較し、前記入力信号が前記しきい値よりも大きい場合、当該入力信号を含むデータセットをサポートベクトルとして採用しないようにするデータ選定手段とを備え、
前記データ選定手段は、過去の所定数の前記入力信号の絶対値に基づいて、前記しきい値を設定する、前置型非線形歪補償器。 - 前記係数更新手段は、
前記変換出力信号を受け、新たに受けた前記変換出力信号の信号列により構成されるベクトルであって、かつ、第2の不感帯の外にあるベクトルをサポートベクトルの候補として抽出し、既にサポートベクトルとして抽出されているベクトルの集合に加え、前記ベクトルの集合を新たにサポートベクトルの集合とみなし、前記ベクトルの集合の中から、前記第1の不感帯の外にあるベクトルをサポートベクトルとして再抽出する抽出手段と、
前記抽出されたサポートベクトルに対する係数を計算する計算手段とを有する、請求項1記載の前置型非線形歪補償器。 - 前記データ選定手段は、所定の期間内の過去の所定数の前記入力信号の絶対値に基づいて、前記しきい値を更新する、請求項1記載の前置型非線形歪補償器。
- 前記信号変換器は、増幅器である、請求項1〜3のいずれかに記載の前置型非線形歪補償器。
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2003157249A JP4281419B2 (ja) | 2003-06-02 | 2003-06-02 | 前置型非線形歪補償器 |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2003157249A JP4281419B2 (ja) | 2003-06-02 | 2003-06-02 | 前置型非線形歪補償器 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| JP2004363733A JP2004363733A (ja) | 2004-12-24 |
| JP4281419B2 true JP4281419B2 (ja) | 2009-06-17 |
Family
ID=34051069
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2003157249A Expired - Fee Related JP4281419B2 (ja) | 2003-06-02 | 2003-06-02 | 前置型非線形歪補償器 |
Country Status (1)
| Country | Link |
|---|---|
| JP (1) | JP4281419B2 (ja) |
Families Citing this family (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP4973532B2 (ja) * | 2008-02-12 | 2012-07-11 | 住友電気工業株式会社 | 増幅回路とこれを有する無線通信装置及びコンピュータプログラム |
| JP2013211616A (ja) * | 2012-03-30 | 2013-10-10 | Sony Corp | 端末装置、端末制御方法、プログラム、および情報処理システム |
| JP6330364B2 (ja) * | 2014-02-26 | 2018-05-30 | ヤマハ株式会社 | 増幅回路の保護回路 |
| WO2019193377A1 (en) * | 2018-04-03 | 2019-10-10 | Nokia Technologies Oy | End-to-end learning in communication systems |
Family Cites Families (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP4183364B2 (ja) * | 1999-12-28 | 2008-11-19 | 富士通株式会社 | 歪補償装置 |
| JP2001268150A (ja) * | 2000-03-21 | 2001-09-28 | Hitachi Kokusai Electric Inc | リニアライザ |
| JP2001284976A (ja) * | 2000-03-29 | 2001-10-12 | Matsushita Electric Ind Co Ltd | アダプティブプリディストーション歪補償方法及び装置 |
| JP4513219B2 (ja) * | 2001-03-06 | 2010-07-28 | 住友電気工業株式会社 | 前置型非線形歪補償器 |
-
2003
- 2003-06-02 JP JP2003157249A patent/JP4281419B2/ja not_active Expired - Fee Related
Also Published As
| Publication number | Publication date |
|---|---|
| JP2004363733A (ja) | 2004-12-24 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| US10897276B2 (en) | Digital predistortion in varying operating conditions | |
| US10931238B2 (en) | Linearization with envelope tracking or average power tracking | |
| US7994856B2 (en) | Predistorter, predistortion method, and predistortion system | |
| JP2009213113A (ja) | 非線形システム逆特性同定装置及びその方法、電力増幅装置及び電力増幅器のプリディストータ | |
| US7412469B2 (en) | Power amplifier pre-distorter training | |
| US8589329B2 (en) | Method and apparatus for incremental tracking of multiple quantiles | |
| CN104363191B (zh) | 一种跳频通信系统的数字预失真方法 | |
| CN102723915B (zh) | 一种适合硬件实现的查询表数字预失真方法和装置 | |
| CN101610093B (zh) | 预失真装置、预失真系统和预失真方法 | |
| CN110765720A (zh) | 一种复值流水线递归神经网络模型的功放预失真方法 | |
| US20120154040A1 (en) | Predistorter for compensating for nonlinear distortion and method thereof | |
| US11817921B2 (en) | System and method for adaptive filtering | |
| US11863210B2 (en) | Linearization with level tracking | |
| JP4281419B2 (ja) | 前置型非線形歪補償器 | |
| CN103929136A (zh) | 宽带移动通信lte系统发射机功率放大器预失真处理方法 | |
| JP3915601B2 (ja) | 前置型非線形歪補償器 | |
| EP2164172B1 (en) | Apparatus and method of compensating distortion | |
| JP4513219B2 (ja) | 前置型非線形歪補償器 | |
| TWI819917B (zh) | 前置補償方法及其前置補償電路 | |
| US20230118004A1 (en) | Power Amplifiers and Methods of Controlling Same | |
| Jia et al. | Centralized Digital Predistortion in 6G: Distributed Task Offloading and Scheduling for Complexity-Reduced PA Linearization | |
| WO2024065725A1 (en) | Methods and apparatuses for perfoming digital predistortion using a combintion model | |
| WO2023115376A1 (en) | Digital pre-distorter for non-linear electronic devices | |
| Chang | An efficient compensation of TWTA's nonlinear distortion in wideband OFDM systems | |
| Kudupudi | High performance Deep Learning based Digital Pre-distorters for RF Power Amplifiers |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| A621 | Written request for application examination |
Free format text: JAPANESE INTERMEDIATE CODE: A621 Effective date: 20060223 |
|
| A977 | Report on retrieval |
Free format text: JAPANESE INTERMEDIATE CODE: A971007 Effective date: 20080805 |
|
| A131 | Notification of reasons for refusal |
Free format text: JAPANESE INTERMEDIATE CODE: A131 Effective date: 20080819 |
|
| A521 | Written amendment |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20080930 |
|
| TRDD | Decision of grant or rejection written | ||
| A01 | Written decision to grant a patent or to grant a registration (utility model) |
Free format text: JAPANESE INTERMEDIATE CODE: A01 Effective date: 20090224 |
|
| A01 | Written decision to grant a patent or to grant a registration (utility model) |
Free format text: JAPANESE INTERMEDIATE CODE: A01 |
|
| A61 | First payment of annual fees (during grant procedure) |
Free format text: JAPANESE INTERMEDIATE CODE: A61 Effective date: 20090309 |
|
| R150 | Certificate of patent or registration of utility model |
Free format text: JAPANESE INTERMEDIATE CODE: R150 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20120327 Year of fee payment: 3 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20120327 Year of fee payment: 3 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20130327 Year of fee payment: 4 |
|
| LAPS | Cancellation because of no payment of annual fees |