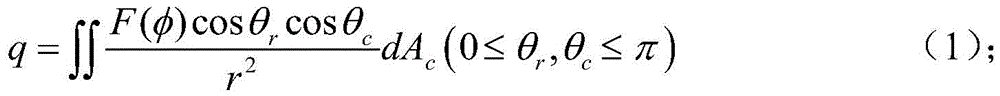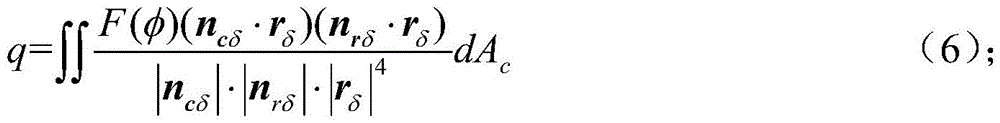CN115292994B - Optical-mechanical coupling method for spherical light energy collection and calculation - Google Patents

Optical-mechanical coupling method for spherical light energy collection and calculation Download PDF

Info

Publication number
CN115292994B
CN115292994B CN202210872627.0A CN202210872627A CN115292994B CN 115292994 B CN115292994 B CN 115292994B CN 202210872627 A CN202210872627 A CN 202210872627A CN 115292994 B CN115292994 B CN 115292994B
Authority
CN
China
Prior art keywords
light
optical
mechanical coupling
condensation
spherical
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Active
Application number
CN202210872627.0A
Other languages
Chinese (zh)
Other versions
CN115292994A (en
Inventor
王东旭
张逸群
段宝岩
李仙丽
樊冠恒
李欣童
杜莹春
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Xidian University
Original Assignee
Xidian University
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Xidian University filed Critical Xidian University
Priority to CN202210872627.0A priority Critical patent/CN115292994B/en
Publication of CN115292994A publication Critical patent/CN115292994A/en
Application granted granted Critical
Publication of CN115292994B publication Critical patent/CN115292994B/en
Active legal-status Critical Current
Anticipated expiration legal-status Critical

Links

Images

Classifications

    • G—PHYSICS
    • G06—COMPUTING; CALCULATING OR COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F30/00—Computer-aided design [CAD]
    • G06F30/20—Design optimisation, verification or simulation
    • G06F30/23—Design optimisation, verification or simulation using finite element methods [FEM] or finite difference methods [FDM]
    • G—PHYSICS
    • G02—OPTICS
    • G02B—OPTICAL ELEMENTS, SYSTEMS OR APPARATUS
    • G02B27/00—Optical systems or apparatus not provided for by any of the groups G02B1/00 - G02B26/00, G02B30/00
    • G02B27/0012—Optical design, e.g. procedures, algorithms, optimisation routines
    • G—PHYSICS
    • G06—COMPUTING; CALCULATING OR COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
    • G06F17/10—Complex mathematical operations
    • G06F17/11—Complex mathematical operations for solving equations, e.g. nonlinear equations, general mathematical optimization problems
    • G06F17/12—Simultaneous equations, e.g. systems of linear equations
    • G—PHYSICS
    • G06—COMPUTING; CALCULATING OR COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
    • G06F17/10—Complex mathematical operations
    • G06F17/16—Matrix or vector computation, e.g. matrix-matrix or matrix-vector multiplication, matrix factorization
    • G—PHYSICS
    • G06—COMPUTING; CALCULATING OR COUNTING
    • G06F—ELECTRIC DIGITAL DATA PROCESSING
    • G06F30/00—Computer-aided design [CAD]
    • G06F30/20—Design optimisation, verification or simulation

Landscapes

  • Engineering & Computer Science (AREA)
  • Physics & Mathematics (AREA)
  • General Physics & Mathematics (AREA)
  • Theoretical Computer Science (AREA)
  • Mathematical Physics (AREA)
  • Computational Mathematics (AREA)
  • Mathematical Analysis (AREA)
  • Mathematical Optimization (AREA)
  • Pure & Applied Mathematics (AREA)
  • Data Mining & Analysis (AREA)
  • General Engineering & Computer Science (AREA)
  • Algebra (AREA)
  • Databases & Information Systems (AREA)
  • Software Systems (AREA)
  • Computer Hardware Design (AREA)
  • Evolutionary Computation (AREA)
  • Geometry (AREA)
  • Operations Research (AREA)
  • Optics & Photonics (AREA)
  • Computing Systems (AREA)
  • Photovoltaic Devices (AREA)
  • Photometry And Measurement Of Optical Pulse Characteristics (AREA)

Abstract

The invention discloses an optical-mechanical coupling method for spherical light energy collection and calculation, which comprises the steps of establishing an optical-mechanical coupling basic model for spherical light condensation, deducing error parameters of structure deformation of a light condensation model, adding the error parameters of structure deformation of the light condensation model into the optical-mechanical coupling basic model, and calculating an optical-mechanical coupling model added with errors by using an integral method to obtain a light distribution result of a light collector receiving surface. The method is adopted to ensure that the calculated light condensing effect is directly hooked with the structural error, so that the result is more accurate.

Description

Optical-mechanical coupling method for spherical light energy collection and calculation
Technical Field
The invention belongs to the technical field of space solar power stations (Space Solar Power Station, SSPS), and relates to an optical-mechanical coupling method for spherical light energy collection and calculation.
Background
Space solar power plants are receiving attention for their continuous and stable energy input and output. With the development of aerospace technology, the establishment of space solar power stations is gradually scheduled, so that more detailed theoretical analysis and experimental verification are required. The space solar power station collects light energy, converts the light energy into electric energy, and then converts the electric energy into microwaves to be emitted to the ground. Wherein light energy collection includes two modes, concentrated and unconcentrated. The concentrating system design is more complex but has a higher power to quality ratio. The lighter the weight and better the space structure is required due to the limitation of the emission cost, the lighter the light condensing structure is used, but generally, the lighter the structure is, the more easily the deformation is. The OMGEA-SSPS solution proposed by the university of Western Anelectron technology team is also in the form of skeleton film development, as the alpha solution proposed by Manchurian in recent years uses a skeleton plus film structure for mass reduction. For film structures with huge light frameworks, the shape surface accuracy is limited. The low accuracy of the condenser lens surface can cause uneven light intensity distribution. For a battery array system, uneven illumination intensity can result in a dramatic decrease in the total energy of the series of cells. For larger battery arrays, serial batteries are necessary, so that the error of the profile of the condenser lens can seriously affect the total generated electric quantity.
For the study of the condensing system with errors, a typical method is that Paul uses cone optics in 1981, describes optical errors by using probability density functions, adds the errors to an optical distribution function, and then uses an angle acceptance function to perform optical analysis calculation. The illumination intensity integral calculation method proposed by Jeter in 1986 lays the foundation for analysis of errors of the reflecting surface. In 1979, the trace tracking method was proposed in combination with the Monte Carlo spot method, and is widely used because of its simple thought and strong adaptability to complex models, and then some people analyze the model with errors by using the method, but calculate the illumination intensity for the condenser model with determined errors, and there is no optical analysis of the direct coupling structure. The main factors causing the uneven illumination intensity after condensation include the incidence angle error of light, the structure error of a condensing lens and the structure error of a receiving surface. The incident angle error is mainly the error caused by the control of the heliostat precision, and can be directly added to the incident angle for calculation. The condensing lens structure and the receiving surface structure have larger influence on condensing effect, and influence on the incident angle and the reflection angle of the condensing lens and the receiving battery, so that the direct introduction and calculation in a calculation formula are more convenient.
In recent years, discipline cross design is more and more important, and coupling design advantages are more obvious. However, the existing optical and structural combination design process is still an independent integrated design, the efficiency and the accuracy are improved, and the optical and thermal analysis is also performed in some documents by using a finite element method and the like, but the coupling analysis is not performed. Errors in the literature are mostly added directly to the incident light, without taking into account the actual structural changes. The structure of the existing ground generally does not consider the quality ratio, has larger mass and good shape retention, so that the structure is reasonable only for the incident light error. However, the space condenser has a complex operation environment, the influence of the structural system on the condensing system needs to be fully considered at the beginning of design, and the influence of the structural error on the condensing effect is directly given out more intuitively and clearly.
Disclosure of Invention
The invention aims to provide an optical-mechanical coupling method for spherical light energy collection and calculation, which introduces structural errors into integral variables in an integral model of spherical light condensation on the basis of deducing the integral model of spherical light condensation, and finally realizes optical-mechanical coupling calculation.
The technical scheme adopted by the invention is that the optical-mechanical coupling method for spherical light energy collection and calculation specifically comprises the following steps:
step 1, establishing a light machine coupling basic model of spherical condensation;
step 2, converting the optical-mechanical coupling basic model established in the step 1 into a vector form;
step 3, calculating an F (phi) reflected light angle function in the optical-mechanical coupling basic model;
step 4, calculating the reflected light ray n in the reflected light ray angle function F (phi) lr ；
Step 5, calculating a structure deformation error delta of a condensation reflecting surface or a condensation receiving surface in the condensation model;
step 6, adding the structural deformation error delta obtained in the step 5 into an optical-mechanical coupling basic model;
and 7, calculating the light distribution result of the light-condensing receiving surface in the optical-mechanical coupling basic model obtained in the step 6 by using an integration method.
The invention is also characterized in that:
the specific process of the step 1 is as follows:
taking two infinitesimal planes d on the light-condensing reflecting surface and the light-condensing receiving surface Ac And d Ar P is d Ar Last point, d Ar Received by d Ac The reflected solar energy is:
Figure BDA0003756888630000031
wherein F (phi) is a reflected ray angle function, theta r Is the connection line of two infinitesimal planes and infinitesimal plane d on the receiving plane Ar Included angle between normal vectors, theta c Representing the connection between two infinitesimal planes and the infinitesimal plane d on the reflecting surface of the condensing reflecting surface Ac The angle between normal vectors, r represents d Ac Distance from p point.
The specific process of the step 2 is as follows:
a infinitesimal surface d arranged on the light-gathering reflection surface Ac N is the normal vector of (2) c Receiving surface infinitesimal surface d Ar N is the normal vector of (2) r ，d Ac And d Ar The vector of the orientation is r, the optical-mechanical coupling basic mode type (1) can be converted into:
Figure BDA0003756888630000041
the specific process of the step 3 is as follows: the reflection angle function F (phi) is calculated using the following equation (3):
Figure BDA0003756888630000042
wherein G is bn The incident light intensity of the aperture plane is s, and the sun opening angle is s. Phi is the reflected light and d Ac And d Ar The included angle between the directional vectors r is specifically expressed as
Figure BDA0003756888630000043
Wherein n is lr Is a reflected light.
The specific process of the step 4 is as follows:
spherical reflected ray n lr From normal n c And incident ray n li Obtaining the normal n c The reflection light n is obtained when the incident light is incident on the vertical caliber surface and is the connection line of the reflection point and the sphere center lr The method comprises the following steps:
n lr ＝2(n c '·n li ')·n c '-n li ' (5)；
wherein n is c '，n li ' n is c ，n li Is a unit vector of (a).
The specific process of the step 5 is as follows: the structural deformation error delta includes a random error delta 1 And systematic error delta 2 The structural deformation error is δ=δ 1 +δ 2 。
The specific process of the step 6 is as follows:
adding a structural error parameter delta into an optical-mechanical coupling model, and assuming that errors delta exist on a condensation reflecting surface and a condensation receiving surface respectively c 、δ r And then correcting the whole optical-mechanical coupling basic model, wherein the corrected formula is as follows:
Figure BDA0003756888630000051
wherein n is cδ ＝n c +δ c ，n rδ ＝n r +δ r ，r δ ＝r+δ r -δ c ，n liδ ＝n li -δ c 。
n lrδ ＝2(n cδ '·n liδ ')·n cδ '-n liδ ' (7)；
Figure BDA0003756888630000052
The beneficial effects of the invention are as follows:
1. the light distribution of spherical condensation can be calculated by using an integral model, and the light distribution is more accurate than a Monte Carlo light trace tracking method;
2. the integration method is more convenient and quick for calculating the spherical condensation, and numerical modification calculation can be directly carried out on the spherical model and the receiving surface model;
3. the method can realize the analysis of the influence of various errors on the condensation performance, and finally realize the condensation system design with high light collection efficiency and high light distribution uniformity continuity by combining the optimization of the actual structural deformation and error utilization model.
Drawings
FIG. 1 is a schematic diagram of spherical condensation;
FIG. 2 shows a micro-element surface d of a spherical condensing reflecting surface in an optical-mechanical coupling method for spherical light energy collection and calculation according to the present invention Ac And receiving a infinitesimal plane d Ar Schematic of the relationship between them;
FIG. 3 is a schematic diagram of vectors of the present invention after adding errors in the optomechanical coupling method for spherical light energy collection calculation;
FIG. 4 is a comparison of the calculated results of the number of divisions of different integration regions in the optomechanical coupling method of the present invention for spherical light energy collection calculation;
FIG. 5 is a comparison of calculation results of different numbers of sampling points in the z-axis direction in the optomechanical coupling method for spherical light energy collection and calculation according to the present invention;
fig. 6 is a calculation result of light distribution after random and systematic errors are added to the optomechanical coupling model in the optomechanical coupling method for spherical light energy collection calculation according to the present invention.
In the figure, 101 is a light condensing reflecting surface and 102 is a light condensing receiving surface.
Detailed Description
The invention will be described in detail below with reference to the drawings and the detailed description.
The invention discloses an optical-mechanical coupling method for spherical light energy collection and calculation, which comprises the steps of establishing an optical-mechanical coupling basic model for spherical light condensation, deducing error parameters of structural deformation of a light condensation model, adding the error parameters of structural deformation of the light condensation model into the optical-mechanical coupling basic model, and calculating an optical-mechanical coupling model added with errors by using an integral method to obtain a light distribution result of a light collector receiving surface.
The invention relates to an optical-mechanical coupling method for spherical light energy collection and calculation, which specifically comprises the following steps:
and step 1, establishing a light machine coupling basic model of spherical condensation.
As shown in fig. 1 and 2, the optomechanical coupling basic model uses the basis ofThe integral of the radiation formula is calculated. Two infinitesimal planes d on the light-condensing reflecting surface 101 and the light-condensing receiving surface 102 are arbitrarily taken Ac And d Ar P is d Ar Last point, d Ar Received by d Ac The reflected solar energy is:
Figure BDA0003756888630000061
wherein F (phi) is a reflected ray angle function, theta r Is the connection line of two infinitesimal planes and infinitesimal plane d on the receiving plane Ar Included angle between normal vectors, theta c Representing the connection between two infinitesimal planes and the infinitesimal plane d on the reflecting surface of the condensing reflecting surface Ac The angle between normal vectors, r represents d Ac Distance from p point.
And 2, converting the optical-mechanical coupling basic model into a vector form, so that the structural error can be conveniently added into the optical-mechanical coupling basic model. A infinitesimal surface d on the condensing reflection surface 101 Ac N is the normal vector of (2) c Receiving surface infinitesimal surface d Ar N is the normal vector of (2) r ，d Ac And d Ar The vector of the orientation is r, the optical-mechanical coupling basic mode type (1) can be converted into:
Figure BDA0003756888630000071
and 3, calculating an F (phi) reflected light angle function in the optical-mechanical coupling basic model. The reflection angle function uses the sun light opening angle relation, and the specific form is as follows:
Figure BDA0003756888630000072
wherein G is bn The incident light intensity of the aperture plane is s, and the sun opening angle is s. Phi is the reflected light and d Ac And d Ar The included angle between the directional vectors r is specifically expressed as
Figure BDA0003756888630000073
Wherein n is lr Is a reflected light.
Step 4, calculating the reflected light ray n in the reflected light ray angle function F (phi) lr . The reflected light of the sphere is calculated by the geometrical optical reflection principle. The spherical reflection light can be reflected by the normal n c And incident ray n li Obtaining the normal n c The reflection light n can be obtained by connecting the reflection point with the sphere center and making the incident light be incident on the vertical caliber surface lr The method comprises the following steps:
n lr ＝2(n c '·n li ')·n c '-n li ' (5)；
wherein n is c '，n li ' n is c ，n li Is a unit vector of (a).
And 5, calculating the structural deformation error delta of the condensation reflecting surface or the condensation receiving surface in the condensation model. The structural deformation errors include random errors delta 1 (directly given from empirical values) and systematic error delta 2 The structural deformation error is δ=δ 1 +δ 2 。
Calculating a systematic error delta in a structural deformation parameter of a condensation model 2 Deformation analysis after load can be performed. The structural statics analysis equation of the condensing reflecting surface and the receiving surface is as follows:
Kδ 2 ＝F (6)；
wherein K is a stiffness matrix, delta 2 The finite element node displacement array is adopted, and F is a node load array. Knowing K and F, delta can be found 2 。
The structural power equation of the condensing reflecting surface or the receiving surface is as follows:
Figure BDA0003756888630000081
wherein M is a mass matrix, C is a damping matrix,
Figure BDA0003756888630000082
the acceleration array and the speed array of the nodes are respectively, and F is a node load array. M, C and F are known to give delta 2 。
And 6, adding a structural deformation error parameter into the optical-mechanical coupling basic model. The structural deformation error of the reflecting surface or the light-condensing receiving surface is delta, and structural error parameters are added into the optical-mechanical coupling model, so that the errors delta of the light-condensing reflecting surface and the light-condensing receiving surface can be assumed to exist c 、δ r As shown in fig. 3, the whole optomechanical coupling basic model is then modified, and the modified formula is:
Figure BDA0003756888630000083
wherein n is cδ ＝n c +δ c ，n rδ ＝n r +δ r ，r δ ＝r+δ r -δ c ，n liδ ＝n li -δ c 。
n lrδ ＝2(n cδ '·n liδ ')·n cδ '-n liδ ' (9)；
Figure BDA0003756888630000091
And 7, coupling and calculating a light distribution result of the light-gathering receiving surface by using an integration method, wherein the integration method uses a common composite simpson integration method.
Example 1
The parameters selected by simulation calculation are that the illumination intensity is 1000W/m < 2 >, the diameter of a spherical condensation reflecting surface of a condensation model is 1m, a hemispherical crown is used for condensation, a hemispherical primary reflecting area is taken, the diameter of a condensation receiving cylindrical surface is 0.1m, and the sun opening angle is 32'. The solar disk has uniform energy distribution, ideal reflectivity and absorptivity, and light rays are perpendicularly incident to the spherical caliber surface. And the deformation error of the structure of the light-condensing reflecting surface or the light-condensing receiving surface in the light-condensing model is zero. The ball reflecting surface and the battery array receiving surface are rotationally symmetrical, so that only the light distribution result on a certain vertical bottom surface straight line on the cylindrical surface can be calculated. In the graph of the calculation result, the abscissa is the height of a straight line perpendicular to the bottom surface on the surface of the light-condensing receiving cylinder, and the ordinate is the illumination intensity.
Fig. 4 shows the results of calculating the division of different integration regions, namely 20×20, 200×200, 500×500, 1000×1000 and 5000×5000, respectively, wherein the higher the number of integration region divisions is, the more accurate the calculation is, but the longer the calculation time is. Fig. 5 shows the calculation results of taking 25 points and 500 points on the straight line of the calculated light-condensing receiving surface, and the more the points are, the more the characterized points are, the more accurate the light intensity change description is.
Example 2
The parameters selected by simulation calculation are that the illumination intensity is 1000W/m < 2 >, the diameter of a spherical condensation reflecting surface of a condensation model is 1m, a hemispherical crown is used for condensation, a hemispherical primary reflecting area is taken, the diameter of a condensation receiving cylindrical surface is 0.1m, and the sun opening angle is 32'. The solar disk has uniform energy distribution, ideal reflectivity and absorptivity, and light rays are perpendicularly incident to the spherical caliber surface. The average value of the random error of the structural deformation of the condensing reflecting surface in the condensing model is 0.1mm, the variance is 0.1mm, and the systematic error is that the condensing reflecting surface is wholly inclined by 1 degree. The ball reflecting surface and the battery array receiving surface are rotationally symmetrical, so that only the light distribution result on a certain vertical bottom surface straight line on the cylindrical surface is calculated. In the graph of the calculation result, the abscissa is the height of a straight line perpendicular to the bottom surface on the surface of the light-condensing receiving cylinder, and the ordinate is the illumination intensity. Fig. 6 shows the calculation result of the light distribution after adding random and systematic errors to the optical-mechanical coupling basic model.

Claims (6)

1. The optical-mechanical coupling method for spherical light energy collection and calculation is characterized in that: the method specifically comprises the following steps:
step 1, establishing a light machine coupling basic model of spherical condensation;
step 2, converting the optical-mechanical coupling basic model established in the step 1 into a vector form;
step 3, calculating an F (phi) reflected light angle function in the optical-mechanical coupling basic model;
step 4, calculating the reflected light ray n in the reflected light ray angle function F (phi) lr ；
Step 5, calculating a structure deformation error delta of a condensation reflecting surface or a condensation receiving surface in the condensation model;
step 6, adding the structural deformation error delta obtained in the step 5 into an optical-mechanical coupling basic model;
the specific process of the step 6 is as follows:
adding a structural error parameter delta into an optical-mechanical coupling model, and assuming that errors delta exist on a condensation reflecting surface and a condensation receiving surface respectively c 、δ r And then correcting the whole optical-mechanical coupling basic model, wherein the corrected formula is as follows:
Figure FDA0004206433960000011
wherein n is cδ ＝n c +δ c ，n rδ ＝n r +δ r ，r δ ＝r+δ r -δ c ，n liδ ＝n li -δ c ；
n lrδ ＝2(n cδ '·n liδ ')·n cδ '-n liδ ' (7)；
Figure FDA0004206433960000012
And 7, calculating the light distribution result of the light-condensing receiving surface in the optical-mechanical coupling basic model obtained in the step 6 by using an integration method.
2. The optomechanical coupling method of claim 1 for spherical light energy collection calculations, wherein: the specific process of the step 1 is as follows:
taking two infinitesimal planes d on the light-condensing reflecting surface and the light-condensing receiving surface Ac And d Ar P is d Ar Last point, d Ar Received by d Ac The reflected solar energy is：
Figure FDA0004206433960000021
Wherein F (phi) is a reflected ray angle function, theta r Is the connection line of two infinitesimal planes and infinitesimal plane d on the receiving plane Ar Included angle between normal vectors, theta c Representing the connection between two infinitesimal planes and the infinitesimal plane d on the reflecting surface of the condensing reflecting surface Ac The angle between normal vectors, r represents d Ac Distance from p point.
3. The optomechanical coupling method of claim 2 for spherical light energy collection calculations, wherein: the specific process of the step 2 is as follows:
a infinitesimal surface d arranged on the light-gathering reflection surface Ac N is the normal vector of (2) c Receiving surface infinitesimal surface d Ar N is the normal vector of (2) r ，d Ac And d Ar The vector of the orientation is r, the optical-mechanical coupling basic mode type (1) can be converted into:
Figure FDA0004206433960000022
4. the optomechanical coupling method of claim 3 for spherical light energy collection calculations, wherein: the specific process of the step 3 is as follows: the reflection angle function F (phi) is calculated using the following equation (3):
Figure FDA0004206433960000023
wherein G is bn The incident light intensity of the aperture surface is s, and the sun opening angle is s; phi is the reflected light and d Ac And d Ar The included angle between the directional vectors r is specifically expressed as
Figure FDA0004206433960000031
Wherein n is lr Is a reflected light.
5. The optomechanical coupling method of claim 4 wherein: the specific process of the step 4 is as follows:
spherical reflected ray n lr From normal n c And incident ray n li Obtaining the normal n c The reflection light n is obtained when the incident light is incident on the vertical caliber surface and is the connection line of the reflection point and the sphere center lr The method comprises the following steps:
n lr ＝2(n c '·n li ')·n c '-n li ' (5)；
wherein n is c '，n li ' n is c ，n li Is a unit vector of (a).
6. The optomechanical coupling method of claim 5 wherein: the specific process of the step 5 is as follows: the structural deformation error delta includes a random error delta 1 And systematic error delta 2 The structural deformation error is δ=δ 1 +δ 2 。
CN202210872627.0A 2022-07-21 2022-07-21 Optical-mechanical coupling method for spherical light energy collection and calculation Active CN115292994B (en)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN202210872627.0A CN115292994B (en) 2022-07-21 2022-07-21 Optical-mechanical coupling method for spherical light energy collection and calculation

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN202210872627.0A CN115292994B (en) 2022-07-21 2022-07-21 Optical-mechanical coupling method for spherical light energy collection and calculation

Publications (2)

Publication Number Publication Date
CN115292994A CN115292994A (en) 2022-11-04
CN115292994B true CN115292994B (en) 2023-06-06

Family

ID=83824769

Family Applications (1)

Application Number Title Priority Date Filing Date
CN202210872627.0A Active CN115292994B (en) 2022-07-21 2022-07-21 Optical-mechanical coupling method for spherical light energy collection and calculation

Country Status (1)

Country Link
CN (1) CN115292994B (en)

Families Citing this family (1)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN116127544B (en) * 2022-11-28 2023-11-03 西安电子科技大学 Modeling method for large-size light condensation error reflecting surface

Citations (2)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN106599504A (en) * 2016-12-23 2017-04-26 西安电子科技大学 Electromechanical coupling model-based space net-shaped antenna power load analysis method
WO2019090958A1 (en) * 2017-11-13 2019-05-16 深圳光峰科技股份有限公司 Light source system and projection device applying light source system

Family Cites Families (3)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
US7081584B2 (en) * 2003-09-05 2006-07-25 Mook William J Solar based electrical energy generation with spectral cooling
CN111191377A (en) * 2020-01-07 2020-05-22 上海索辰信息科技有限公司 Nonlinear fitting method in optical-mechanical thermal coupling
KR20220112831A (en) * 2020-12-14 2022-08-11 구글 엘엘씨 Feedback controller using secret share

Patent Citations (2)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN106599504A (en) * 2016-12-23 2017-04-26 西安电子科技大学 Electromechanical coupling model-based space net-shaped antenna power load analysis method
WO2019090958A1 (en) * 2017-11-13 2019-05-16 深圳光峰科技股份有限公司 Light source system and projection device applying light source system

Also Published As

Publication number Publication date
CN115292994A (en) 2022-11-04

Similar Documents

Publication Publication Date Title
Wang et al. Experimental study and optical analyses of a multi-segment plate (MSP) concentrator for solar concentration photovoltaic (CPV) system
CN102519152B (en) Calculating method for mirror field optical efficiency on basis of graphics processing unit (GPU) tower type solar energy thermoelectric system
CN102645686B (en) Design method of uniformly-converging Fresnel lens
Xie et al. Theoretical and experimental analysis on efficiency factors and heat removal factors of Fresnel lens solar collector using different cavity receivers
CN115292994B (en) Optical-mechanical coupling method for spherical light energy collection and calculation
WO2018059243A1 (en) Apparatus for collecting and transmitting solar energy, and method therefor
CN110442959B (en) Method for predicting and maintaining light-gathering performance of solar disc type light-gathering system
CN108225552B (en) Method for measuring concentration energy flux density distribution of heliostat field in tower-type power station
CN105509339B (en) A kind of scope of freedom Opticai Concentrating System With Secondary Reflection efficiently changed for solar heat/electricity
CN112685943B (en) Method and system for predicting condensation performance of umbrella-shaped flexible stretched film condenser
CN109460594B (en) Method for predicting light-gathering performance of disc type triangular element spliced parabolic film condenser
CN109945518B (en) Solar heat/electricity combined light path gathering method
CN117421884A (en) Calculation method for optical efficiency of mirror field of tower type solar photo-thermal power station
Wang et al. Analysis of space-based large light concentration reflective surfaces with errors
CN101388418B (en) Portable non-track type non-image forming solar condensing device
Wu et al. Comparative study on heat flux and temperature distribution performance of linear Fresnel collector based on uniformity index
CN109992882B (en) Monte Carlo ray tracing-based solar radiation energy density simulation method
CN114329903A (en) Method for calculating shadow efficiency of heliostat of tower-type solar photothermal power station
CN107145473B (en) Method for calculating heliostat surface type micro-arc angle
CN116127544B (en) Modeling method for large-size light condensation error reflecting surface
Sanchez Enhancing concentration ratio of solar concentrators
CN111898292B (en) Spherical condenser supporting method for space solar power station
WO2019232917A1 (en) Curved light-concentrating reflector and processing system thereof, and light-concentrating reflector set and manufacturing method thereof
Xu et al. Research on optimization model based on heliostat field
CN115951485A (en) Free-form surface reflector array design method of solar light condensing device

Legal Events

Date Code Title Description
PB01 Publication
PB01 Publication
SE01 Entry into force of request for substantive examination
SE01 Entry into force of request for substantive examination
GR01 Patent grant
GR01 Patent grant