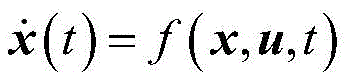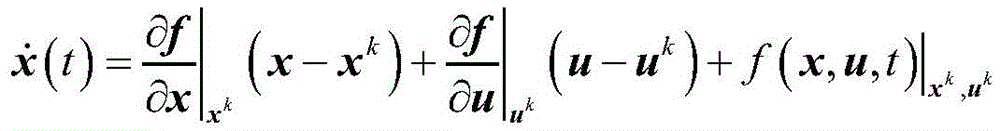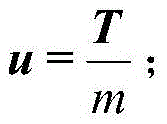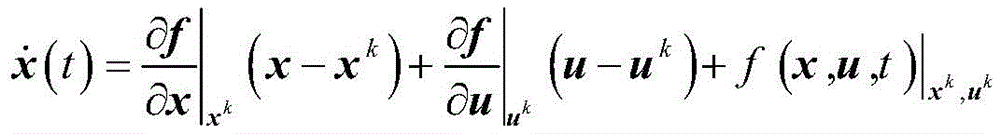CN111301720B - Deep space probe track autonomous control method - Google Patents
Deep space probe track autonomous control method Download PDFInfo
- Publication number
- CN111301720B CN111301720B CN202010212525.7A CN202010212525A CN111301720B CN 111301720 B CN111301720 B CN 111301720B CN 202010212525 A CN202010212525 A CN 202010212525A CN 111301720 B CN111301720 B CN 111301720B
- Authority
- CN
- China
- Prior art keywords
- control
- detector
- track
- orbit
- nominal
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Expired - Fee Related
Links
- 238000000034 method Methods 0.000 title claims abstract description 66
- 239000000523 sample Substances 0.000 title claims abstract description 29
- 238000005457 optimization Methods 0.000 claims abstract description 36
- 238000012546 transfer Methods 0.000 claims abstract description 15
- 238000013461 design Methods 0.000 claims abstract description 6
- 238000005096 rolling process Methods 0.000 claims description 21
- 238000012545 processing Methods 0.000 claims description 9
- RZVHIXYEVGDQDX-UHFFFAOYSA-N 9,10-anthraquinone Chemical compound C1=CC=C2C(=O)C3=CC=CC=C3C(=O)C2=C1 RZVHIXYEVGDQDX-UHFFFAOYSA-N 0.000 claims description 6
- 238000004422 calculation algorithm Methods 0.000 claims description 6
- 239000000446 fuel Substances 0.000 claims description 4
- 230000001133 acceleration Effects 0.000 claims description 3
- 230000001141 propulsive effect Effects 0.000 claims description 2
- 206010048669 Terminal state Diseases 0.000 abstract description 2
- 238000012937 correction Methods 0.000 description 4
- 238000004364 calculation method Methods 0.000 description 3
- 238000005259 measurement Methods 0.000 description 2
- 238000004891 communication Methods 0.000 description 1
- 238000011217 control strategy Methods 0.000 description 1
- 238000001514 detection method Methods 0.000 description 1
- 238000010586 diagram Methods 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 238000011160 research Methods 0.000 description 1
- 238000004088 simulation Methods 0.000 description 1
Images
Classifications
-
- B—PERFORMING OPERATIONS; TRANSPORTING
- B64—AIRCRAFT; AVIATION; COSMONAUTICS
- B64G—COSMONAUTICS; VEHICLES OR EQUIPMENT THEREFOR
- B64G1/00—Cosmonautic vehicles
- B64G1/22—Parts of, or equipment specially adapted for fitting in or to, cosmonautic vehicles
- B64G1/24—Guiding or controlling apparatus, e.g. for attitude control
- B64G1/242—Orbits and trajectories
-
- B—PERFORMING OPERATIONS; TRANSPORTING
- B64—AIRCRAFT; AVIATION; COSMONAUTICS
- B64G—COSMONAUTICS; VEHICLES OR EQUIPMENT THEREFOR
- B64G1/00—Cosmonautic vehicles
- B64G1/22—Parts of, or equipment specially adapted for fitting in or to, cosmonautic vehicles
- B64G1/24—Guiding or controlling apparatus, e.g. for attitude control
- B64G1/244—Spacecraft control systems
- B64G1/247—Advanced control concepts for autonomous, robotic spacecraft, e.g. by using artificial intelligence, neural networks or autonomous agents
Landscapes
- Engineering & Computer Science (AREA)
- Remote Sensing (AREA)
- Automation & Control Theory (AREA)
- Combustion & Propulsion (AREA)
- Radar, Positioning & Navigation (AREA)
- Aviation & Aerospace Engineering (AREA)
- Chemical & Material Sciences (AREA)
- Health & Medical Sciences (AREA)
- Artificial Intelligence (AREA)
- Evolutionary Computation (AREA)
- General Health & Medical Sciences (AREA)
- Medical Informatics (AREA)
- Robotics (AREA)
- Control Of Position, Course, Altitude, Or Attitude Of Moving Bodies (AREA)
- Feedback Control In General (AREA)
Abstract
The invention discloses an autonomous control method for a deep space probe orbit, and belongs to the technical field of aerospace. The implementation method of the invention comprises the following steps: dispersing the nominal orbit of the known optimized design to obtain discretization data of the nominal orbit state and the control quantity; for the current control period, obtaining the estimation state of the detector at the later moment according to the estimation value of the navigation system; then, the current state is used as an initial value of the orbit, the terminal state of the nominal orbit is used as a target value, the optimal control problem is solved by adopting a sequence convex optimization method, and the detector transfer orbit is re-planned to obtain a new orbit control law; the detector executes the track control according to the new control instruction in the control period until reaching the next control moment. And repeating the iteration of the steps until the terminal moment is reached, and ending the autonomous control of the track. The invention has the following advantages: the optimal control problem is solved by utilizing convex optimization, the speed is high, the convergence is strong, the robustness is good, and the obtained solution is the global optimal solution.
Description
Technical Field
The invention relates to an autonomous control method for a deep space probe orbit, and belongs to the technical field of aerospace.
Background
The deep space probe is influenced by various factors such as emission errors, navigation errors, thruster execution errors and the like in the interplanetary flight process and gradually deviates from a preset design track, so that the probe cannot reach a target position, and the detection task fails; on the other hand, the deep space probe is far away from the ground measurement and control station in the task process, the communication time is long, and the track control of the probe cannot be implemented by a ground measurement and control system. Therefore, it is required that the deep space probe has an autonomous orbit control capability. With the increasingly urgent need of deep space exploration tasks for the autonomy of detectors, the research of the autonomous control method of the deep space detector orbit is one of the hot problems in the aerospace field at present.
In the developed autonomous control method for the deep space probe track, in the prior art [1] (Shanghai Bian, jin Ting, Wangshuai, et al. interplanetary small-thrust track guidance strategy based on B plane parameters [ J ]. academic newspaper of Beijing university of science and engineering, 2013,33 (11)), a closed-loop prediction guidance algorithm based on target B plane parameters is adopted. And taking the B plane parameter as target constraint, establishing the relation between the target B plane parameter and the discrete guidance parameter, and realizing the correction of the guidance parameter by adopting a segmented successive correction strategy based on a differential correction thought. The method adopts the B plane parameter as the guidance target constraint, improves the guidance precision of the small thrust transfer orbit, but has poor robustness, and is difficult to correct the orbit when the deviation value of the actual orbit and the nominal orbit is large.
In the prior art [2] (Starek J A, Kolmanovsky I V.nonlinear model predictive Control strategies for low thrust space flight simulations [ J ]. Optimal Control Applications and Methods,2014,35(1):1-20.), a model predictive Control method is adopted to solve the inter-planet transfer problem of the low thrust of the detector, a track correction method taking an Optimal track as reference is researched, the minimum fuel consumption is taken as a target, the current state is taken as an initial condition to carry out track re-planning, and a sequence quadratic planning algorithm is used to solve the Optimal Control problem of the track. The entire track is discretized into a series of control subintervals over which the control law becomes piecewise linear. The method has good robustness, but the optimal control law is solved by utilizing the traditional nonlinear programming algorithm, the calculation speed is low, and the autonomous control requirement cannot be met.
Disclosure of Invention
Aiming at the problems of poor robustness, low speed of solving the optimal control problem and the like of the existing method, the invention discloses an autonomous control method for a deep space probe track, which aims to solve the technical problems that: the method for the deep space probe track model predictive control based on the convex optimization idea is provided, the track optimal control problem can be solved relatively quickly when the track is re-planned, the requirement of autonomous control on-line implementation is met, meanwhile, the convex optimization has strong convergence and good robustness, and the obtained solution is the global optimal solution.
The purpose of the invention is realized by the following technical scheme.
The invention discloses an autonomous control method for a deep space probe track, which is characterized in that a nominal track with known optimal design is dispersed to obtain discretization data of a nominal track state and a control quantity; for the current control period, obtaining the estimation state of the detector at the later moment according to the estimation value of the navigation system; then, the current state is used as an initial value of the orbit, the terminal state of the nominal orbit is used as a target value, the optimal control problem is solved by adopting a sequence convex optimization method, and the detector transfer orbit is re-planned to obtain a new orbit control law; the detector executes the track control according to the new control instruction in the control period until reaching the next control moment. And repeating the iteration of the steps until the terminal moment is reached, and ending the autonomous control of the track.
The invention discloses an autonomous control method for a deep space probe track, which comprises the following steps:
the method comprises the following steps of firstly, dispersing a nominal orbit of the known optimized design to obtain discretization data of the nominal orbit state and the control quantity.
The method comprises the following steps of establishing a track dynamics model of the deep space probe:
wherein: r, v, m respectively represent the position, speed and mass of the detector; t is a three-dimensional thrust vector of the detector; mu represents a solar attraction coefficient, alphafuelIs the detector mass consumption rate.
Because the thrust generated by the detector propulsion system is limited, the modular length of the three-dimensional thrust vector of the detector should meet the following constraint conditions:
||T||≤Tmax
Knowing the nominal orbital state xrefAnd a control quantity urefStart time t of nominal orbit0And terminal time tfDividing the nominal track by N to obtain the control period delta T ═ T (T)f-t0) and/N, namely realizing discretization processing of the nominal track state and the control quantity to obtain discretization data of the nominal track state and the control quantity.
And step two, respectively predicting the track state in each track control period.
For the ith (i ═ 1,2, …, N) control cycle, the start time is tiObtaining t from the navigation system estimateiEstimated state x (t) of the time of day detectori) Namely, the track state prediction is realized.
And step three, defining a rolling optimal control problem P1 needing to be solved, carrying out convex processing on the rolling optimal control problem P1 based on a sequence convex optimization method to obtain a convex model P2 of the rolling optimal control problem P1, solving the optimal control problem P2 by adopting the sequence convex optimization method, and re-planning the transfer orbit of the detector to obtain a new orbit control law.
In order to make the actual flight trajectory of the probe close to the nominal trajectory while enabling the probe to reach the target position at a predetermined time, when solving this problem using the model predictive control method, for each control node, the following rolling optimal control problem P1 needs to be solved:
performance indexes are as follows:
constraint conditions are as follows:
x(ti)=xi
x(tf)=xf
||u||≤umax
wherein: function f (x, u, t)) Is a compact form of the dynamic equation of the detector, and the maximum propulsion acceleration umaxRespectively according to the nominal orbit and the actual task requirement.
Based on a sequence convex optimization method, carrying out convex processing on the rolling optimal control problem P1 by adopting Taylor series expansion to obtain a rolling optimal control convex model P2 of the rolling optimal control problem P1:
performance indexes are as follows:
constraint conditions are as follows:
x(ti)=xi
x(tf)=xf
||u||≤umax
||x-xk||+||u-uk||≤ρ
wherein: rho represents a confidence domain of an approximate convex optimization problem solution in a sequence convex optimization algorithm, and the confidence domain is added into a performance index, so that the convergence speed of the convex optimization method can be improved, and the risks of divergence and iteration interruption of the convex optimization method can be reduced.
Solving an optimal control problem P2 by adopting a sequence convex optimization method, and re-planning the detector transfer orbit to obtain a new orbit control law u (t), ti≤t≤tf;
Step four, the detector executes orbit control according to the control instruction obtained in the step three in the ith control period corresponding to the step two until the detector completes the flight control task in the ith control period, and the command t is senti+1=ti+ Δ T, return to step two.
The detector obtains a control instruction u (t), t in the ith control period corresponding to the step two according to the step threei≤t≤ti+ Δ T execution trajectory controlAnd c, controlling until the detector completes the flight control task in the ith control period, and controlling ti+1=ti+ Δ T, return to step two.
And step five, repeating the iteration steps from the step two to the step four until the autonomous control of the track is terminated.
Solving the optimal control problem by adopting a sequence convex optimization method, and re-planning the detector transfer orbit to obtain an updated orbit control law; the detector executes the orbit control according to the updated control instruction within the control period until reaching the next control moment. Repeating the above steps, and when t isi+1=tfThe orbit autonomous control terminates.
Has the advantages that:
the invention discloses an autonomous control method for a deep space probe track, which is characterized in that a model predictive control method is used for predicting the subsequent state of the deep space probe in the flight process, the optimal control problem of the track is solved through a sequence convex optimization method, the probe transfer track is re-planned, the convergence and the robustness are improved through the convex optimization method, and an updated track control law is obtained. In addition, the optimal control problem of the track is solved by a convex optimization method, the solving speed of the optimization problem can be improved, and the requirement of autonomous control is met.
Drawings
FIG. 1 is a flow chart of the autonomous control method of the deep space probe orbit of the invention;
FIG. 2 is a diagram of the Earth-Mars low thrust transfer orbit in accordance with an embodiment.
Detailed Description
For a better understanding of the objects and advantages of the present invention, reference should be made to the following detailed description taken in conjunction with the accompanying drawings and examples.
Example 1:
as shown in fig. 2, the embodiment discloses an autonomous control method for a deep space probe track, which includes the following specific steps:
the method comprises the following steps of firstly, dispersing a nominal orbit of the known optimized design to obtain discretization data of the nominal orbit state and the control quantity.
The method comprises the following steps of establishing a track dynamics model of the deep space probe:
wherein: r, v, m respectively represent the position, speed and mass of the detector; t is a three-dimensional thrust vector of the detector; mu represents a solar attraction coefficient, alphafuelIs the detector mass consumption rate.
Because the thrust generated by a detector propulsion system is limited, the modular length of the three-dimensional thrust vector of the detector should meet the following constraint conditions:
||T||≤Tmax
Knowing the nominal orbital state xrefAnd a control quantity urefStart time t of nominal orbit0And terminal time tfDividing the nominal orbit by 50 equal parts to obtain a control period delta T=(tf-t0) And/50, realizing discretization processing of the nominal track state and the control quantity to obtain discretization data of the nominal track state and the control quantity.
Initial point state of the track:
r0=[-60544412.47 -138973011.01 10293.07]km
v0=[29.63140060 -14.81280821 -1.50550590]km/s
track end point state:
rf=[-73275056.62 229357920.17 6603202.14]km
vf=[-21.70480986 -9.31009855 0.98008222]km/s;
and step two, respectively predicting the track state in each track control period.
For the ith (i ═ 1,2, …, N) control cycle, the start time is tiObtaining t from the navigation system estimateiEstimated state x (t) of the time of day detectori) Namely, the track state prediction is realized.
And step three, defining a rolling optimal control problem P1 needing to be solved, carrying out convex processing on the rolling optimal control problem P1 based on a sequence convex optimization method to obtain a convex model P2 of the rolling optimal control problem P1, solving the optimal control problem P2 by adopting the sequence convex optimization method, and re-planning the transfer orbit of the detector to obtain a new orbit control law.
In order to make the actual flight trajectory of the probe close to the nominal trajectory while enabling the probe to reach the target position at a predetermined time, when solving this problem using the model predictive control method, for each control node, the following rolling optimal control problem P1 needs to be solved:
performance indexes are as follows:
constraint conditions are as follows:
x(ti)=xi
x(tf)=xf
||u||≤umax
wherein: the function f (x, u, t) is a compact form of the detector kinetic equation, the maximum propulsive acceleration umaxThe value was 5.93X 10-6km/s2。
Based on a sequence convex optimization method, carrying out convex processing on the rolling optimal control problem P1 by adopting Taylor series expansion to obtain a rolling optimal control convex model P2 of the rolling optimal control problem P1:
performance indexes are as follows:
constraint conditions are as follows:
x(ti)=xi
x(tf)=xf
||u||≤umax
||x-xk||+||u-uk||≤ρ
wherein: rho represents a confidence domain of an approximate convex optimization problem solution in a sequence convex optimization algorithm, and the confidence domain is added into a performance index, so that the convergence speed of the convex optimization method can be improved, and the risks of divergence and iteration interruption of the convex optimization method can be reduced.
Solving an optimal control problem P2 by adopting a sequence convex optimization method, and re-planning the detector transfer orbit to obtain a new orbit control law u (t), ti≤t≤tf;
Step four, the detector executes orbit control according to the control instruction obtained in the step three in the ith control period corresponding to the step two until the detector completes the flight control task in the ith control period, and the command t is senti+1=ti+ Δ T, return to step two.
The detector obtains a control instruction u (t), t in the ith control period corresponding to the step two according to the step threei≤t≤tiExecuting orbit control by + delta T until the detector completes the flight control task in the ith control period, and enabling Ti+1=ti+ Δ T, return to step two.
And step five, repeating the iteration steps from the step two to the step four, and stopping the autonomous control of the track.
Solving the optimal control problem by adopting a sequence convex optimization method, and re-planning the detector transfer orbit to obtain an updated orbit control law; the detector executes the orbit control according to the updated control instruction within the control period until reaching the next control moment. Continuously repeating the above steps when ti+1=tfThe orbit autonomous control terminates. On the whole trackIn the main control process, the minimum control period is selected to be 431136s, the single maximum calculation time is 5.2s, the ratio of the calculation time to the control period is not more than 0.002%, and the autonomous control requirement is met.
The above detailed description is intended to illustrate the objects, aspects and advantages of the present invention, and it should be understood that the above detailed description is only exemplary of the present invention and is not intended to limit the scope of the present invention, and any modifications, equivalents, improvements and the like made within the spirit and principle of the present invention should be included in the scope of the present invention.
Claims (1)
1. A deep space probe track autonomous control method is characterized by comprising the following steps: comprises the following steps of (a) carrying out,
dispersing a nominal track of known optimal design to obtain discretization data of the nominal track state and the control quantity;
step two, respectively predicting the track state in each track control period;
step three, defining a rolling optimal control problem P1 needing to be solved, carrying out convex processing on the rolling optimal control problem P1 based on a sequence convex optimization method to obtain a convex model P2 of the rolling optimal control problem P1, solving an optimal control problem P2 by adopting the sequence convex optimization method, and re-planning a detector transfer track to obtain a new track control law;
step four, the detector executes orbit control according to the control instruction obtained in the step three in the ith control period corresponding to the step two until the detector completes the flight control task in the ith control period, and the command t is senti+1=ti+ Δ T, where TiIs the start time, t, of the ith control cyclei+1The starting time of the (i + 1) th control period is set, delta T is the control period, and the step two is returned;
step five, repeating the iteration steps from the step two to the step four until the autonomous control of the track is terminated;
the first implementation method comprises the following steps of,
the method comprises the following steps of establishing a track dynamics model of the deep space probe:
wherein: r, v, m respectively represent the position, speed and mass of the detector; t is a three-dimensional thrust vector of the detector; mu represents a solar attraction coefficient, alphafuelIs the detector mass consumption rate;
because the thrust generated by the detector propulsion system is limited, the modular length of the three-dimensional thrust vector of the detector should meet the following constraint conditions:
||T||≤Tmax
Knowing the nominal orbital state xrefAnd a control quantity urefStart time t of nominal orbit0And terminal time tfDividing the nominal track by N to obtain the control period delta T ═ T (T)f-t0) The method comprises the following steps that/N, namely discretization processing of a nominal track state and a control quantity is realized, and discretization data of the nominal track state and the control quantity are obtained;
the second step is realized by the method that,
for the ith (i ═ 1,2, …, N) control cycle, the start time is tiObtaining t from the navigation system estimateiEstimated state x (t) of the time of day detectori) Namely, the track state prediction is realized;
the third step is to realize the method as follows,
in order to make the actual flight trajectory of the probe close to the nominal trajectory while enabling the probe to reach the target position at a predetermined time, when solving this problem using the model predictive control method, for each control node, the following rolling optimal control problem P1 needs to be solved:
performance indexes are as follows:
constraint conditions are as follows:
x(ti)=xi
x(tf)=xf
||u||≤umax
wherein: the function f (x, u, t) is a compact form of the detector kinetic equation, the maximum propulsive acceleration umaxRespectively obtaining the track data according to the nominal track and the actual task requirement;
based on a sequence convex optimization method, carrying out convex processing on the rolling optimal control problem P1 by adopting Taylor series expansion to obtain a rolling optimal control convex model P2 of the rolling optimal control problem P1:
performance indexes are as follows:
constraint conditions are as follows:
x(ti)=xi
x(tf)=xf
||u||≤umax
||x-xk||+||u-uk||≤ρ
wherein: rho represents a confidence domain of an approximate convex optimization problem solution in a sequence convex optimization algorithm, and the confidence domain is added into a performance index, so that the convergence speed of the convex optimization method can be improved, and the risks of divergence and iteration interruption of the convex optimization method can be reduced;
by using sequencesSolving an optimal control problem P2 by a convex optimization method, and re-planning the transfer orbit of the detector to obtain a new orbit control law u (t), ti≤t≤tf;
The implementation method of the fourth step is that,
the detector obtains a control instruction u (t), t in the ith control period corresponding to the step two according to the step threei≤t≤tiExecuting orbit control by + delta T until the detector completes the flight control task in the ith control period, and enabling Ti+1=ti+ Δ T, return to step two;
the fifth step is to realize that the method is that,
solving the optimal control problem by adopting a sequence convex optimization method, and re-planning the detector transfer orbit to obtain an updated orbit control law; the detector executes track control according to the updated control instruction in the control period until reaching the next control moment; repeating the above steps, and when t isi+1=tfThe orbit autonomous control terminates, where tfIs the terminal time.
Applications Claiming Priority (2)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202010051829 | 2020-01-17 | ||
| CN202010051829X | 2020-01-17 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN111301720A CN111301720A (en) | 2020-06-19 |
| CN111301720B true CN111301720B (en) | 2021-09-03 |
Family
ID=71157203
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202010212525.7A Expired - Fee Related CN111301720B (en) | 2020-01-17 | 2020-03-24 | Deep space probe track autonomous control method |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN111301720B (en) |
Families Citing this family (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN114137993B (en) * | 2021-11-01 | 2022-07-29 | 北京空间飞行器总体设计部 | Ground fire short transfer orbit launching window searching method with deep space maneuver |
Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN106407619A (en) * | 2016-11-16 | 2017-02-15 | 哈尔滨工业大学 | Linear-feedback global stabilization method for controlling limited spacecraft rendezvous control system |
| CN109250153A (en) * | 2018-12-04 | 2019-01-22 | 北京理工大学 | Martian atmosphere approach section track optimal tracking method of guidance |
Family Cites Families (9)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US7861975B2 (en) * | 2006-03-31 | 2011-01-04 | The Boeing Company | Two part spacecraft servicing vehicle system with universal docking adaptor |
| US8489260B2 (en) * | 2008-12-16 | 2013-07-16 | California Institute Of Technology | Method and apparatus for powered descent guidance |
| CN103455707A (en) * | 2013-07-22 | 2013-12-18 | 西北工业大学 | Finite-thrust driven spacecraft automatic-rendezvous trajectory planning method on basis of convex optimization technology |
| US9216745B2 (en) * | 2013-09-16 | 2015-12-22 | Disney Enterprises, Inc. | Shared control of semi-autonomous vehicles including collision avoidance in multi-agent scenarios |
| EP3622439B1 (en) * | 2017-09-15 | 2022-08-03 | Google LLC | Improvements related to generating a robot control policy from demonstrations collected via kinesthetic teaching of a robot |
| EP3506041A1 (en) * | 2017-12-29 | 2019-07-03 | Deutsches Zentrum für Luft- und Raumfahrt e.V. | Method, apparatus and spacecraft for constrained atmospheric entry |
| CN109543284B (en) * | 2018-11-20 | 2022-10-04 | 北京理工大学 | Mars atmosphere entry section optimal guidance method based on Kriging spatial interpolation |
| CN110414125B (en) * | 2019-07-25 | 2022-09-13 | 哈尔滨工业大学 | Event-driven spacecraft rendezvous fault diagnosis and filter design method |
| CN110562493B (en) * | 2019-09-06 | 2021-03-30 | 北京理工大学 | Mars power descending trajectory planning method based on vector trajectory |
-
2020
- 2020-03-24 CN CN202010212525.7A patent/CN111301720B/en not_active Expired - Fee Related
Patent Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN106407619A (en) * | 2016-11-16 | 2017-02-15 | 哈尔滨工业大学 | Linear-feedback global stabilization method for controlling limited spacecraft rendezvous control system |
| CN109250153A (en) * | 2018-12-04 | 2019-01-22 | 北京理工大学 | Martian atmosphere approach section track optimal tracking method of guidance |
Also Published As
| Publication number | Publication date |
|---|---|
| CN111301720A (en) | 2020-06-19 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| Lu | Entry guidance: a unified method | |
| Huang et al. | A survey of numerical algorithms for trajectory optimization of flight vehicles | |
| Mease et al. | Reduced-order entry trajectory planning for acceleration guidance | |
| Wang et al. | Entry trajectory planning with terminal full states constraints and multiple geographic constraints | |
| Xie et al. | Highly constrained entry trajectory generation | |
| Pan et al. | 3D guidance for hypersonic reentry gliders based on analytical prediction | |
| Slegers et al. | Terminal guidance of autonomous parafoils in high wind-to-airspeed ratios | |
| CN112550770B (en) | Rocket soft landing trajectory planning method based on convex optimization | |
| CN106114910B (en) | A kind of spacecraft flight track roll stablized loop method | |
| CN106444822A (en) | Space vector field guidance based stratospheric airship's trajectory tracking control method | |
| Zhang et al. | Entry guidance for high-L/D hypersonic vehicle based on drag-vs-energy profile | |
| CN113900448B (en) | Aircraft prediction correction composite guidance method based on sliding mode interference observer | |
| Dominguez Calabuig et al. | Optimal on-board abort guidance based on successive convexification for atmospheric re-entry | |
| CN103224023B (en) | Phase plane self-adaptation control method based on characteristic model | |
| CN104567545A (en) | Guidance method for endoatmospheric powered phase of RLV (reusable launch vehicle) | |
| CN111301720B (en) | Deep space probe track autonomous control method | |
| CN114370793A (en) | Rocket sublevel return and vertical landing guidance method | |
| Sharma et al. | Pseudo-spectral MPSP-based unified midcourse and terminal guidance for reentry targets | |
| Lorenz et al. | A decoupled approach for trajectory generation for an unmanned rotorcraft | |
| CN104950668A (en) | Analytical fuel optimizing control method and analytical fuel optimizing control system for satellite formation | |
| CN110209190B (en) | Satellite nominal orbit unbiased flight control method | |
| Chen et al. | Steady Glide Dynamics and Guidance of Hypersonic Vehicle | |
| CN116049993A (en) | Three-dimensional analytic guidance method and device for boosting section of carrier rocket and electronic equipment | |
| Zheng et al. | Model predictive static programming rendezvous trajectory generation of unmanned aerial vehicles | |
| Herrera et al. | Uav target tracking using nonlinear model predictive control |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant | ||
| CF01 | Termination of patent right due to non-payment of annual fee | ||
| CF01 | Termination of patent right due to non-payment of annual fee |
Granted publication date: 20210903 |