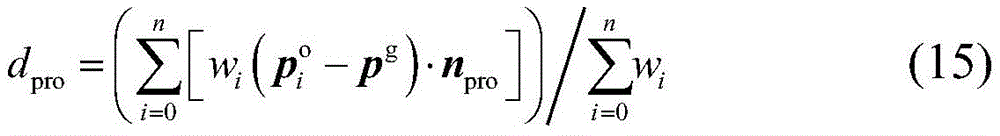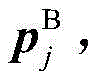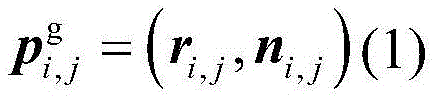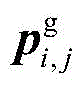CN109683552B - Numerical control machining path generation method on complex point cloud model guided by base curve - Google Patents

Numerical control machining path generation method on complex point cloud model guided by base curve Download PDF

Info

Publication number
CN109683552B
CN109683552B CN201811427216.0A CN201811427216A CN109683552B CN 109683552 B CN109683552 B CN 109683552B CN 201811427216 A CN201811427216 A CN 201811427216A CN 109683552 B CN109683552 B CN 109683552B
Authority
CN
China
Prior art keywords
point
point cloud
boundary
projection
curve
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Active
Application number
CN201811427216.0A
Other languages
Chinese (zh)
Other versions
CN109683552A (en
Inventor
徐金亭
徐隆坤
耿真
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Dalian University of Technology
Original Assignee
Dalian University of Technology
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Dalian University of Technology filed Critical Dalian University of Technology
Priority to CN201811427216.0A priority Critical patent/CN109683552B/en
Publication of CN109683552A publication Critical patent/CN109683552A/en
Application granted granted Critical
Publication of CN109683552B publication Critical patent/CN109683552B/en
Active legal-status Critical Current
Anticipated expiration legal-status Critical

Links

Images

Classifications

    • G—PHYSICS
    • G05—CONTROLLING; REGULATING
    • G05B—CONTROL OR REGULATING SYSTEMS IN GENERAL; FUNCTIONAL ELEMENTS OF SUCH SYSTEMS; MONITORING OR TESTING ARRANGEMENTS FOR SUCH SYSTEMS OR ELEMENTS
    • G05B19/00—Programme-control systems
    • G05B19/02—Programme-control systems electric
    • G05B19/18—Numerical control [NC], i.e. automatically operating machines, in particular machine tools, e.g. in a manufacturing environment, so as to execute positioning, movement or co-ordinated operations by means of programme data in numerical form
    • G05B19/19—Numerical control [NC], i.e. automatically operating machines, in particular machine tools, e.g. in a manufacturing environment, so as to execute positioning, movement or co-ordinated operations by means of programme data in numerical form characterised by positioning or contouring control systems, e.g. to control position from one programmed point to another or to control movement along a programmed continuous path
    • Y—GENERAL TAGGING OF NEW TECHNOLOGICAL DEVELOPMENTS; GENERAL TAGGING OF CROSS-SECTIONAL TECHNOLOGIES SPANNING OVER SEVERAL SECTIONS OF THE IPC; TECHNICAL SUBJECTS COVERED BY FORMER USPC CROSS-REFERENCE ART COLLECTIONS [XRACs] AND DIGESTS
    • Y02—TECHNOLOGIES OR APPLICATIONS FOR MITIGATION OR ADAPTATION AGAINST CLIMATE CHANGE
    • Y02P—CLIMATE CHANGE MITIGATION TECHNOLOGIES IN THE PRODUCTION OR PROCESSING OF GOODS
    • Y02P90/00—Enabling technologies with a potential contribution to greenhouse gas [GHG] emissions mitigation
    • Y02P90/02—Total factory control, e.g. smart factories, flexible manufacturing systems [FMS] or integrated manufacturing systems [IMS]

Landscapes

  • Engineering & Computer Science (AREA)
  • Human Computer Interaction (AREA)
  • Manufacturing & Machinery (AREA)
  • Physics & Mathematics (AREA)
  • General Physics & Mathematics (AREA)
  • Automation & Control Theory (AREA)
  • Numerical Control (AREA)

Abstract

The invention belongs to the technical field of numerical control machining, and discloses a method for generating a numerical control machining path on a complex point cloud model guided by a base curve. Firstly, extracting and sequencing boundary points of point cloud to form an ordered boundary point sequence curve, and then dividing the ordered boundary point sequence curve into four boundary point sequence curves; constructing a Kosky curved surface according to the four point sequence curves and constructing a guide curve on the base surface; then, offsetting the point cloud by taking the radius of the ball end mill as an offset distance; establishing a least square projection model from a guide point to a point cloud, and giving a weight determination method and a projection direction calculation strategy of a working point of the model; iteratively projecting the guide curve onto the offset point cloud along the calculated projection direction, thereby generating an interference-free tool path. The method of the invention passes through the complex construction process from the point cloud data to the CAD parameter model, and directly carries out tool path planning based on the measured point cloud, thereby effectively shortening the production and manufacturing period from the measurement of the prototype of the part to the manufacture of the part and reducing the cost of processing and manufacturing.

Description

Numerical control machining path generation method on complex point cloud model guided by base curve
Technical Field
The invention belongs to the technical field of numerical control machining, and particularly relates to a method for generating a numerical control machining path on a complex point cloud model guided by a base curve.
Background
At present, with the rapid development of 3D scanning devices, dense and accurate point clouds can represent the geometry of the physical prototype of a part more finely, and have been applied to various industries, such as Reverse Engineering (RE), Rapid Prototyping (RP), and the like. In order to realize the rapid manufacturing of the physical prototypes of the parts, the traditional processing process is to firstly obtain the measurement point cloud of the part prototype by using contact or non-contact measurement equipment, then reconstruct a parameter CAD model from the point cloud data, and plan a numerical control machining tool path on the CAD model. But reconstruction of the parametric CAD model from the measured data is a complex and time consuming process that accounts for over 60% of the entire design, manufacturing cycle. Although current commercial CAD software such as CATIA, Imageware, etc. provides a reverse design function from point cloud data to a parametric surface, the complex area segmentation of point cloud, splicing and clipping between area patches, approximation accuracy and continuity control depending on the experience of designers, and inevitable model repeated modification caused thereby have severely limited the realization and operation of the numerical control processing method based on the parametric surface when facing the point cloud data and the practical application in manufacturing enterprises. The method goes beyond the complicated construction process from discrete data to a parameter curved surface, and the method for realizing the high-efficiency numerical control machining of the complex curved surface part directly based on the point cloud data is undoubtedly an effective way for breaking through the problems. The chinese invention patent "a tool path direct generation method based on measured data" applied by the present invention by the jangege et al generates a tool path for numerical control machining by using a directional projection method (patent No. CN 102608954 a), but the method is significantly different from the hole-s-base plane and iterative least square projection method which are used by the present invention and can better reflect the shape and characteristics of a curved surface. The document "Zhang YJ, Ge LL.adaptive tool pathgeneration on point-sample surfaces.precis Eng 2011; 591-601. A level set-based point projection technique is proposed to directly generate a tool path on the point cloud. The literature "Liu Y, Xia S, Qian X. direct Numerical Control (NC) path generation from discrete points to continuous points paths ASME Trans, J Computt Inf Sci Eng 2012; 031002-1-12' proposes a method based on moving least squares surface projection. At present, a point cloud model-based numerical control machining path generation method at home and abroad mainly converts scattered point cloud data into a simple Z-map or triangular mesh model, and then generates a tool path by using a cross-section method. The proposed method based on level set projection and moving least square plane projection is also significantly different from the method of the invention of point cloud direct least square iterative projection. The invention aims to find a method for directly generating a tool track on a point cloud measured by a contact or non-contact scanning device, which does not relate to nonlinear optimization and has simple and intuitive mathematical calculation process, overcomes the construction process of a point cloud data CAD parameter model, avoids some problems in the process of model conversion, can effectively shorten the development period of a new product and the production and manufacturing period from the measurement of a part prototype to the manufacture of the part, and reduces the processing and manufacturing cost.
Disclosure of Invention
In order to overcome the defects of the existing method for generating the processing path on the point cloud model, the invention provides a method for generating the numerical control processing path on the complex point cloud model guided by a base curve, and the method for generating the processing path directly based on point cloud data is realized.
The technical scheme of the invention is as follows:
a method for generating a numerical control machining path on a complex point cloud model guided by a base curve comprises the following steps:
step a, extracting boundary points of point cloud and sequencing the boundary points to form an ordered boundary point sequence curve, and then dividing the ordered boundary point sequence curve into four boundary point sequence curves;
the method comprises the following specific steps:
a1. selecting any point p on the point cloud, and establishing a local coordinate system by taking p as an origin, wherein the coordinate system comprises
Figure GDA0002260714450000021
Is p points and its K neighborhood point set CK(p) a unit vector of a line direction of any one point,
Figure GDA0002260714450000022
is p points and its K neighborhood point set CK(p) the unit normal vector of the fitted plane,
Figure GDA0002260714450000031
is that
Figure GDA0002260714450000032
And
Figure GDA0002260714450000033
a vector product of (a);
a2. set K neighborhood points CK(p) projection onto
Figure GDA0002260714450000034
Obtaining a projection point set C in the planeK pro(p) for any one point
Figure GDA0002260714450000035
Figure GDA0002260714450000036
Representing point p and point
Figure GDA0002260714450000037
Connecting line and shaft of
Figure GDA0002260714450000038
The angle of (d);
a3. calculating all included angles
Figure GDA0002260714450000039
And the difference between two consecutive angles
Figure GDA00022607144500000310
If the maximum angular difference
Figure GDA00022607144500000311
Exceeding a specified angle threshold
Figure GDA00022607144500000312
Then the point p is the boundary point;
a4. sorting the boundary points: finding any point in the boundary point set as the starting boundary point
Figure GDA00022607144500000313
Find its closest point in the set of boundary points
Figure GDA00022607144500000314
Then the vector is processed
Figure GDA00022607144500000315
Search direction as next boundary point
Figure GDA00022607144500000316
a5. Order to
Figure GDA00022607144500000317
Then along the search direction
Figure GDA00022607144500000325
Finding distances in a set of boundary points
Figure GDA00022607144500000318
Nearest boundary point
Figure GDA00022607144500000319
Then order
Figure GDA00022607144500000320
Updating search directions
Figure GDA00022607144500000321
Until the initial boundary point is searched
Figure GDA00022607144500000322
Then the process is terminated;
b, constructing a Kouski curved surface according to the four boundary point sequence curves and constructing a guide curve on the base surface;
the construction equation for the guide curve points is as follows:
Figure GDA00022607144500000323
in the formula, ri,jDenotes the jth guide point, n, on the ith guide curvei,jA unit normal vector representing the guide point on the base plane;
c, offsetting the point cloud by taking the radius of the ball end mill as an offset distance;
d, establishing a least square projection model from the guide point to the point cloud, determining a projection direction and a weight of a working point participating in calculation of the projection point, and iteratively projecting a guide curve onto the offset point cloud along the calculated projection direction to generate an interference-free tool path;
the method comprises the following specific steps:
d1. the plane least squares projection model of the point-to-point cloud model on the guide curve is:
Figure GDA00022607144500000324
in the formula, pgIn order to guide the curve points,
Figure GDA0002260714450000041
is point cloud data, wiIs a data point
Figure GDA0002260714450000042
The relevant weight factor is determined by formula (5);
d2. e (d) in formula (2)pro) The condition for obtaining the minimum value is dE (d)pro)/dd pro0, thus obtaining dproComprises the following steps:
Figure GDA0002260714450000043
d3. the projection direction is as follows:
Figure GDA0002260714450000044
in the formula:
Figure GDA0002260714450000045
representing the direction vector of the projection, ni,jThe unit normal vector of the guide point on the base plane is represented,
Figure GDA0002260714450000046
representing closest approach on a point cloud
Figure GDA0002260714450000047
Point of (2)
Figure GDA0002260714450000048
The unit normal vector of (1);
d4. weight factor wjDetermined as follows:
Figure GDA0002260714450000049
in the formula (I), the compound is shown in the specification,
Figure GDA00022607144500000410
as a guide curve point pgAnd operating point
Figure GDA00022607144500000411
The distance between the two adjacent electrodes is less than the total distance,
Figure GDA00022607144500000412
is composed of
Figure GDA00022607144500000413
And a projection line LpThe distance of (d);
d5. and iteratively projecting the guide curve onto the offset point cloud along the calculated projection direction, and terminating iteration when the difference value of two iterations meets the given error precision or reaches the maximum iteration times.
Compared with the prior art, the invention has the beneficial effects that: the invention directly constructs the cutter path based on the measured point cloud, and overcomes the process of point cloud data surface fitting, thereby effectively shortening the production and manufacturing period from the measurement of the part prototype to the manufacture of the part and reducing the design and manufacturing cost.
Drawings
FIG. 1 is a flow chart of the method of the present invention.
FIG. 2 is a schematic diagram of the extraction of point cloud boundary data points.
FIG. 3(a) is a schematic diagram of the ordering of scattered data points.
Fig. 3(b) is a schematic diagram of the division of four boundary point sequence curves.
Fig. 4(a) - (c) are schematic diagrams of point cloud biasing.
Fig. 5 is a schematic diagram of projection direction calculation.
Fig. 6 is an example of the obtained processing path.
Detailed Description
The flow chart of the numerical control machining path generation method on the complex point cloud model guided by the base curve is shown in figure 1. The following detailed description of the embodiments of the invention is provided in conjunction with the accompanying drawings and the implementation steps:
step 1, extracting boundary data points of the point cloud.
Step 1.1. first of allSelecting any point p on the point cloud, and establishing a local coordinate system ξ with p as the origin(L)The position of the lens is determined, in a coordinate system,
Figure GDA0002260714450000051
is p points and its K neighborhood point set CK(p) a unit vector of a line direction of any one point,
Figure GDA0002260714450000052
is the unit normal vector of the plane to which the p points and their K neighborhood point sets are fitted,
Figure GDA0002260714450000053
is that
Figure GDA0002260714450000054
And
Figure GDA0002260714450000055
is calculated as the vector product of (a).
Step 1.2, set C of K neighborhood pointsK(p) projection onto
Figure GDA0002260714450000056
On the plane, obtaining a projection point set CK pro(p) for any one point
Figure GDA0002260714450000057
Figure GDA0002260714450000058
Representing point p and point
Figure GDA0002260714450000059
Connecting line and shaft of
Figure GDA00022607144500000510
Is represented by the following formula:
Figure GDA00022607144500000511
step 1.3. calculate neighborhood point set CK(p) angle of each point
Figure GDA00022607144500000512
And calculating the difference between two consecutive angles
Figure GDA00022607144500000513
If the maximum angular difference
Figure GDA00022607144500000514
Exceeding a specified angle threshold
Figure GDA00022607144500000515
Figure GDA00022607144500000516
The point p is a boundary point. FIG. 2 is a schematic diagram of extracting boundary data points.
Step 1.4, searching all points on the point cloud according to the steps to obtain a boundary point set
Figure GDA00022607144500000517
And 2, sequencing the boundary data points. Selecting any point in the set of boundary points
Figure GDA0002260714450000061
As starting boundary point
Figure GDA0002260714450000062
Then, sorting the scattered boundary points according to the following steps:
step 2.1. set of boundary points
Figure GDA0002260714450000063
In searching for distance points
Figure GDA0002260714450000064
Nearest point
Figure GDA0002260714450000065
Then the vector is processed
Figure GDA0002260714450000066
Search direction as next boundary point
Figure GDA0002260714450000067
As shown in fig. 3 (a).
Step 2.2. order
Figure GDA0002260714450000068
Then along the search direction
Figure GDA0002260714450000069
Finding distance
Figure GDA00022607144500000610
Nearest boundary point
Figure GDA00022607144500000611
At the same time
Figure GDA00022607144500000612
The following should be satisfied:
Figure GDA00022607144500000613
wherein theta isthIs a specified angle threshold.
Step 2.3, if the formula (3) is true, make
Figure GDA00022607144500000614
Updating search directions
Figure GDA00022607144500000615
Step 2.4. until the initial boundary point is searched
Figure GDA00022607144500000616
And terminating, otherwise, jumping to step 2.2 to continue searching.
Step 3, constructing a Coons base curved surface and a guide curve
Step 3.1, four corner points are designated through interactive operation, the sorted boundary curve obtained in the step 2 is divided into 4 sections of Point Sequence Curves (PSC) by using the four corner points, and as shown in fig. 3(B), each section is fitted by using a cubic B-spline curve:
Figure GDA00022607144500000617
wherein u is more than or equal to 0, v is less than or equal to 1, r0(u)、r1(u)、r0(v) And r1(v) The compatibility condition of the node vector is satisfied.
The four corner points satisfy the following conditions:
Figure GDA00022607144500000618
and 3.2, constructing the Coons basal plane through bilinear interpolation of the four boundary curves. The simplest bilinear Coons surface is represented as follows:
r(u,v)＝s1(u,v)+s2(u,v)-s3(u,v)(6)
wherein s is1(u, v) and s2(u, v) are each located at r0(u) and r1(u) and r0(v) And r1(v) Linear lofting curve between, s3(u, v) is a tensor product surface, which is a bilinear surface defined by the four corner points in equation (5).
And 3.3, constructing a guide curve point. The construction equation for the guide curve points is as follows:
Figure GDA0002260714450000071
wherein r isi,jDenotes the jth guide point, n, on the ith guide curvei,jThe unit normal vector of the guide point on the base plane is represented. Record the ith PSC guide curve
Figure GDA0002260714450000072
Step 4. offset of point cloud
In order to avoid the machining interference between the cutter and the point cloud model, the radius of the cutter of the ball end mill is used as an offset distance for offset, and the offset direction of each data point is the normal direction of the point.
And 4.1, in order to estimate the normal direction of each data point in the point cloud, calculating the covariance matrix of the point set in the K neighborhood of the point. Let CK(p) represents the K neighborhood set of points for point p, then its 3 x 3 covariance matrix HpCalculated from the following formula:
Figure GDA0002260714450000073
wherein q isj∈CK(p), j ═ 1, …, k. To HpSingular value decomposition is carried out, then HpThe eigenvector corresponding to the minimum eigenvalue is the normal vector n of the p pointpI.e. np＝emin. Fig. 4(a) shows the normal vector of the point cloud calculated by the above method.
And 4.2, unifying the directions of the normals, and enabling all the normals to point to the processing side of the point cloud, as shown in fig. 4 (b). Firstly, the normal direction of a point cloud angular point p is consistent with the normal direction of a corresponding angular point on a base surface, and then the normal direction of each neighborhood point of the point p is adjusted, so that the angle between the normal direction of the point p and the normal direction of each neighborhood point of the point p does not exceed a specified angle threshold:
Figure GDA0002260714450000074
wherein n isp，nneigRespectively the normal directions of the p-point and its neighbours,
Figure GDA0002260714450000075
is an angle threshold, typically less than pi/2 in magnitude.
Step 4.3. offset P of point cloudoffsetCan be calculated from the following formula:
Poffset:po＝p+npRc(10)
wherein is RcRadius of the ball nose cutter. FIG. 4(c) is a schematic diagram illustrating the offset of the point cloud
And 5, calculating the projection direction, wherein the projection direction is determined by the following formula as shown in FIG. 5:
Figure GDA0002260714450000081
in the formula
Figure GDA0002260714450000082
Representing the direction vector of the projection, ni,jThe unit normal vector of the guide point on the base plane is represented,
Figure GDA0002260714450000083
representing closest approach on a point cloud
Figure GDA0002260714450000084
Point of (2)
Figure GDA0002260714450000085
The unit normal vector of (2).
And 6, establishing a least square projection model from the guide point to the point cloud, and determining a weight factor of the working point.
And 6.1, representing the projection of the guide curve point on the offset point cloud along the projection direction as follows:
qpro＝pg+dpronpro(12)
in the formula, qproAs projected points to be solved, dproRepresenting the projection distance, nproIndicating the projection direction.
Step 6.2, a least square projection model from the guide curve point to the point cloud is as follows:
Figure GDA0002260714450000086
in the formula (I), wherein
Figure GDA0002260714450000087
Is point cloud data, wiIs a data point
Figure GDA0002260714450000088
Is determined by equation (16).
Step 6.3 objective function E (d) in equation (13)pro) The conditions for obtaining the minimum value are:
Figure GDA0002260714450000089
this makes it possible to obtain:
Figure GDA00022607144500000810
step 6.4 weight factor wiDetermined by the following formula
Figure GDA0002260714450000091
In the formula (I), the compound is shown in the specification,
Figure GDA0002260714450000092
for points to be projected
Figure GDA0002260714450000093
And a guide curve point pgThe distance between the two or more of the two or more,
Figure GDA0002260714450000094
is composed of
Figure GDA0002260714450000095
And a projection line LpThe distance of (c). The projection curve equation is as follows:
Lp＝pg+tnpro(17)
and 7, iteratively calculating projection points from the guide curve points to the point cloud, and sequentially connecting the projection points to form a tool path.
Step 7.1, selecting the offset point cloud as an initial working point setP0Calculating the projection point q using the equations (12) and (15)pro；
Step 7.2, calculating weight factor { w ] in the first iteration according to the public indication (18)iThreshold value w of }limit；
Figure GDA0002260714450000096
In the formula, wmeanAnd wmaxAre respectively all weight factors { wiMean and maximum of.
Step 7.3, if the point P in the working point setlWeight factor w ofjGreater than a threshold value wlimitIf yes, keeping the working point set; otherwise, deleting the operation point from the operation point set, thereby updating the operation point set;
and 7.4, calculating projection points in the (l + 1) th iteration according to the new working point set
Figure GDA0002260714450000097
And calculates the following iteration end criteria:
Figure GDA0002260714450000098
or l > Kmax(19)
In the formula, epsilonprFor a given accuracy of calculation, KmaxIs the maximum number of iterations. If the iteration termination criterion is met, the iteration is terminated; otherwise, updating the point to be projected to
Figure GDA0002260714450000099
The iteration process continues until the iteration termination criteria are met.
In conclusion, the invention directly constructs the cutter path based on the measured point cloud, and the process from point cloud data to CAD parameter model construction is passed, so that the production period from the measurement of the part prototype to the processing and manufacturing of the part can be effectively shortened, and the design and manufacturing cost is reduced. The high-efficiency tool motion mode can be planned more conveniently on a simple base surface, so that the tool can perform high-efficiency processing on the most appropriate path topology on the point cloud.

Claims (1)

1. A numerical control machining path generation method on a complex point cloud model guided by a base curve is characterized by comprising the following steps:
step a, extracting boundary points of point cloud and sequencing the boundary points to form an ordered boundary point sequence curve, and then dividing the ordered boundary point sequence curve into four boundary point sequence curves;
the method comprises the following specific steps:
a1. selecting any point p on the point cloud, and establishing a local coordinate system by taking p as an origin, wherein the coordinate system comprises
Figure FDA0002313996670000011
Is p points and its K neighborhood point set CK(p) a unit vector of a line direction of any one point,
Figure FDA0002313996670000012
is p points and its K neighborhood point set CK(p) the unit normal vector of the fitted plane,
Figure FDA0002313996670000013
is that
Figure FDA0002313996670000014
And
Figure FDA0002313996670000015
a vector product of (a);
a2. set K neighborhood points CK(p) projection onto
Figure FDA0002313996670000016
Obtaining a projection point set C in the planeK pro(p) for any one point
Figure FDA0002313996670000017
Figure FDA0002313996670000018
Representing point p and point
Figure FDA0002313996670000019
Connecting line and shaft of
Figure FDA00023139966700000110
The angle of (d);
a3. calculating all included angles
Figure FDA00023139966700000111
And the difference between two consecutive angles
Figure FDA00023139966700000112
If the maximum angular difference
Figure FDA00023139966700000113
Exceeding a specified angle threshold
Figure FDA00023139966700000114
Then the point p is the boundary point;
a4. sorting the boundary points: finding any point in the boundary point set as the starting boundary point
Figure FDA00023139966700000115
Find its closest point in the set of boundary points
Figure FDA00023139966700000116
Then the vector is processed
Figure FDA00023139966700000117
Search direction as next boundary point
Figure FDA00023139966700000118
a5. Order to
Figure FDA00023139966700000119
Then along the search direction
Figure FDA00023139966700000120
Finding distances in a set of boundary points
Figure FDA00023139966700000121
Nearest boundary point
Figure FDA00023139966700000122
Then order
Figure FDA00023139966700000123
Updating search directions
Figure FDA00023139966700000124
Until the initial boundary point is searched
Figure FDA00023139966700000125
Then the process is terminated;
b, constructing a Kouski curved surface according to the four boundary point sequence curves and constructing a guide curve on the base surface;
the construction equation for the guide curve points is as follows:
Figure FDA00023139966700000126
in the formula, ri,jDenotes the jth guide point, n, on the ith guide curvei,jA unit normal vector representing the guide point on the base plane;
c, offsetting the point cloud by taking the radius of the ball end mill as an offset distance;
d, establishing a least square projection model from the guide point to the point cloud, determining a projection direction and a weight of a working point participating in calculation of the projection point, and iteratively projecting a guide curve onto the offset point cloud along the calculated projection direction to generate an interference-free tool path;
the method comprises the following specific steps:
d1. the plane least squares projection model of the point-to-point cloud model on the guide curve is:
Figure FDA0002313996670000021
in the formula, pgIn order to guide the curve points,
Figure FDA0002313996670000022
is point cloud data, wiIs a data point
Figure FDA0002313996670000023
A related weight factor; dproRepresenting the projection distance, nproRepresenting a projection direction;
d2. e (d) in formula (2)pro) The condition for obtaining the minimum value is dE (d)pro)/ddpro0, thus obtaining dproComprises the following steps:
Figure FDA0002313996670000024
d3. the projection direction is as follows:
Figure FDA0002313996670000025
in the formula:
Figure FDA0002313996670000026
representing the direction vector of the projection, ni,jThe unit normal vector of the guide point on the base plane is represented,
Figure FDA0002313996670000027
representing closest approach on a point cloud
Figure FDA0002313996670000028
Point of (2)
Figure FDA0002313996670000029
The unit normal vector of (1);
d4. weight factor wjDetermined as follows:
Figure FDA00023139966700000210
in the formula (I), the compound is shown in the specification,
Figure FDA00023139966700000211
as a guide curve point pgAnd operating point
Figure FDA00023139966700000212
The distance between the two adjacent electrodes is less than the total distance,
Figure FDA00023139966700000213
is composed of
Figure FDA00023139966700000214
And a projection line LpThe distance of (d);
d5. and iteratively projecting the guide curve onto the offset point cloud along the calculated projection direction, and terminating iteration when the difference value of two iterations meets the given error precision or reaches the maximum iteration times.
CN201811427216.0A 2018-11-27 2018-11-27 Numerical control machining path generation method on complex point cloud model guided by base curve Active CN109683552B (en)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN201811427216.0A CN109683552B (en) 2018-11-27 2018-11-27 Numerical control machining path generation method on complex point cloud model guided by base curve

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN201811427216.0A CN109683552B (en) 2018-11-27 2018-11-27 Numerical control machining path generation method on complex point cloud model guided by base curve

Publications (2)

Publication Number Publication Date
CN109683552A CN109683552A (en) 2019-04-26
CN109683552B true CN109683552B (en) 2020-04-28

Family

ID=66185625

Family Applications (1)

Application Number Title Priority Date Filing Date
CN201811427216.0A Active CN109683552B (en) 2018-11-27 2018-11-27 Numerical control machining path generation method on complex point cloud model guided by base curve

Country Status (1)

Country Link
CN (1) CN109683552B (en)

Families Citing this family (7)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
JP6713700B1 (en) * 2020-03-09 2020-06-24 リンクウィズ株式会社 Information processing method, information processing system, program
JP6849262B1 (en) * 2020-05-28 2021-03-24 リンクウィズ株式会社 Information processing method, information processing system, program
CN111806720B (en) * 2020-06-24 2021-12-07 成都飞机工业（集团）有限责任公司 Rectification skin construction method based on measured data of wing body butt joint
CN114055253B (en) * 2021-11-16 2023-06-30 四川航天长征装备制造有限公司 Process characteristic measurement construction and processing method for large complex surface part
CN114089692B (en) * 2021-11-18 2024-04-19 江苏科技大学 Quick numerical control programming method suitable for complex slender surfaces of parts
CN115830269B (en) * 2022-12-08 2023-06-06 中铁工程设计咨询集团有限公司 Tunnel point cloud normal direction adjustment method, device, equipment and readable access medium
CN118428696B (en) * 2024-07-01 2024-08-27 中川建投集团有限公司 Civil engineering cost control method based on big data analysis

Family Cites Families (5)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
JP4809488B1 (en) * 2010-05-24 2011-11-09 ファナック株式会社 Numerical control device with oscillating function capable of changing speed in any section
CN102608954A (en) * 2012-03-26 2012-07-25 西安交通大学 Method for directly generating tool path based on measured data
CN106054802B (en) * 2016-07-28 2019-04-26 电子科技大学 A kind of free-form surface self-adaptive Toolpath Generation method
CN106354098B (en) * 2016-11-04 2018-09-04 大连理工大学 A kind of NURBS composite surfaces are fixed a cutting tool teeth processing route generating method
CN108319224B (en) * 2018-03-13 2019-08-13 大连理工大学 A kind of multiaxis NC maching spiral path generation method based on diametral curve interpolation

Also Published As

Publication number Publication date
CN109683552A (en) 2019-04-26

Similar Documents

Publication Publication Date Title
CN109683552B (en) Numerical control machining path generation method on complex point cloud model guided by base curve
CN110516388B (en) Harmonic mapping-based curved surface discrete point cloud model circular cutter path generation method
JP4934789B2 (en) Interpolation processing method and interpolation processing apparatus
CN112284290B (en) Autonomous measurement method and system for aero-engine blade robot
JP5436416B2 (en) Approximation processing method and approximation processing apparatus
ElKott et al. Isoparametric line sampling for the inspection planning of sculptured surfaces
CN114055255B (en) Large-scale complex component surface polishing path planning method based on real-time point cloud
Li et al. Arc–surface intersection method to calculate cutter–workpiece engagements for generic cutter in five-axis milling
CN113276130B (en) Free-form surface spraying path planning method and system based on point cloud slice
CN108682043A (en) A kind of complex-curved measure planning method based on parameter mapping
CN112033338B (en) Blade curved surface contact type scanning measurement probe radius surface compensation method
Sieger et al. A comprehensive comparison of shape deformation methods in evolutionary design optimization
CN109597354A (en) A kind of multiple constraint numerical control processing track generation method of triangle grid model
CN109343468A (en) A kind of blade multiaxis orbit generation method based on projection biasing
Jamiolahmadi et al. Study of detailed deviation zone considering coordinate metrology uncertainty
CN114611359A (en) Grid-parameter hybrid model modeling method and system
Liu et al. High precision measurement of blade profile curve using iterative normal vector approximation
Xu et al. A method of generating spiral tool path for direct three-axis computer numerical control machining of measured cloud of point
Xu et al. A new welding path planning method based on point cloud and deep learning
Zhang et al. Efficient sampling method based on co-kriging for free-form surface measurement
CN112381945B (en) Reconstruction method and system of three-dimensional model transition surface
CN112687010A (en) Digital metering method for end frame drill jig
Gong et al. Research on discretization algorithm of free-form surface for robotic polishing
CN116360337A (en) Point cloud data-based numerical control machining contour parallel tool path generation method
CN111474899A (en) Triangular-based complex cavity high-speed numerical control milling spiral path generation method

Legal Events

Date Code Title Description
PB01 Publication
PB01 Publication
SE01 Entry into force of request for substantive examination
SE01 Entry into force of request for substantive examination
GR01 Patent grant
GR01 Patent grant