CN109584324B - Positron Emission Tomography (PET) reconstruction method based on automatic encoder network - Google Patents
Positron Emission Tomography (PET) reconstruction method based on automatic encoder network Download PDFInfo
- Publication number
- CN109584324B CN109584324B CN201811247856.3A CN201811247856A CN109584324B CN 109584324 B CN109584324 B CN 109584324B CN 201811247856 A CN201811247856 A CN 201811247856A CN 109584324 B CN109584324 B CN 109584324B
- Authority
- CN
- China
- Prior art keywords
- image
- dae
- network
- pet
- automatic encoder
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
- 238000000034 method Methods 0.000 title claims abstract description 48
- 238000002600 positron emission tomography Methods 0.000 title claims abstract description 36
- 238000007476 Maximum Likelihood Methods 0.000 claims description 9
- 238000001514 detection method Methods 0.000 claims description 7
- 239000011159 matrix material Substances 0.000 claims description 7
- 238000005259 measurement Methods 0.000 claims description 5
- 230000008569 process Effects 0.000 claims description 5
- 230000004044 response Effects 0.000 claims description 4
- 238000012935 Averaging Methods 0.000 claims description 3
- 238000013178 mathematical model Methods 0.000 claims description 3
- 238000010606 normalization Methods 0.000 claims description 3
- 238000012549 training Methods 0.000 claims description 3
- 238000002591 computed tomography Methods 0.000 abstract description 8
- 230000000694 effects Effects 0.000 abstract description 5
- 230000006870 function Effects 0.000 description 6
- 238000004458 analytical method Methods 0.000 description 3
- 238000009499 grossing Methods 0.000 description 3
- 230000004913 activation Effects 0.000 description 2
- 238000010586 diagram Methods 0.000 description 2
- 229910052704 radon Inorganic materials 0.000 description 2
- SYUHGPGVQRZVTB-UHFFFAOYSA-N radon atom Chemical compound [Rn] SYUHGPGVQRZVTB-UHFFFAOYSA-N 0.000 description 2
- PXFBZOLANLWPMH-UHFFFAOYSA-N 16-Epiaffinine Natural products C1C(C2=CC=CC=C2N2)=C2C(=O)CC2C(=CC)CN(C)C1C2CO PXFBZOLANLWPMH-UHFFFAOYSA-N 0.000 description 1
- 206010028980 Neoplasm Diseases 0.000 description 1
- 210000003484 anatomy Anatomy 0.000 description 1
- 238000013528 artificial neural network Methods 0.000 description 1
- 230000009286 beneficial effect Effects 0.000 description 1
- 238000004364 calculation method Methods 0.000 description 1
- 238000003759 clinical diagnosis Methods 0.000 description 1
- 238000013461 design Methods 0.000 description 1
- 230000007613 environmental effect Effects 0.000 description 1
- 238000001914 filtration Methods 0.000 description 1
- 238000003384 imaging method Methods 0.000 description 1
- 230000036039 immunity Effects 0.000 description 1
- 238000001727 in vivo Methods 0.000 description 1
- 230000004060 metabolic process Effects 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 238000012545 processing Methods 0.000 description 1
- 238000011160 research Methods 0.000 description 1
- 238000006467 substitution reaction Methods 0.000 description 1
- 238000012360 testing method Methods 0.000 description 1
- 238000011282 treatment Methods 0.000 description 1
Images
Classifications
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T11/00—2D [Two Dimensional] image generation
- G06T11/003—Reconstruction from projections, e.g. tomography
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T2211/00—Image generation
- G06T2211/40—Computed tomography
- G06T2211/424—Iterative
Landscapes
- Physics & Mathematics (AREA)
- General Physics & Mathematics (AREA)
- Engineering & Computer Science (AREA)
- Theoretical Computer Science (AREA)
- Nuclear Medicine (AREA)
Abstract
The invention provides a Positron Emission Tomography (PET) reconstruction method based on an automatic encoder network, which comprises the following steps: step A: establishing a Denoising Automatic Encoder (DAE) network model on the basis of a positron emission computed tomography (PET) image, and acquiring prior information of the image by using a trained Denoising Automatic Encoder (DAE); and B: the invention integrates a Denoising Automatic Encoder (DAE) network based on a Positron Emission Tomography (PET) reconstruction method, adopts the Denoising Automatic Encoder (DAE) network to learn the prior information of the PET image without supervision, then combines the DAE network with the image prior information with the traditional PET iterative reconstruction method, and alternately iterates the two to obtain the reconstructed image, thereby achieving good reconstruction effect.
Description
Technical Field
The invention relates to the technical field of medical image processing, which is mainly used in the fields of denoising, recovering, reconstructing and the like of electronic Computed Tomography (CT), positron emission computed tomography (PET), medical noisy images, and the like, in particular to a positron emission computed tomography (PET) reconstruction method based on an automatic encoder network.
Background
Positron Emission Tomography (PET) is currently the only new imaging technique that can display biomolecular metabolism, receptor and neuromediator activity in vivo, and is an important tool for tumor research and clinical diagnosis and treatment. PET reconstruction is a method of reconstructing a functional image acceptable to a clinician from low-tech-rate and noise-affected projection sinusoidal data. Due to the detector fuzzy effect, positron range and photon nonlinearity, the existing PET reconstructed image has the problems of poor resolution, unclear anatomical structure, inaccurate anatomical positioning, large Poisson noise and the like. At the same time, the limited number of photons in the PET data requires spatial smoothing to reduce noise.
In PET reconstruction, the measurement data y ∈ R M×1 Can be modeled as an independent Poisson randomSet of machine variables by affine transformationAnd unknown image x ∈ R N×1 The relationship of (a) to (b) is as follows:P∈R M×N is a detection probability matrix, P ij Representing the probability of detecting a photon originating from voxel j by detector i. s is formed by R M×1 And R ∈ R M×1 Respectively, representing scatter coincidence and random coincidence data. M is the number of lines of response (LOR) and N is the number of pixels in image space.
PET reconstruction methods include analytical methods and iterative methods. The analytic methods may be classified into a filtered back projection method (FBP), a back projection filtering method (BFP), a ρ -filter, a convolution back projection method, and the like, according to a specific calculation process. Most representative is a filtered back projection method, an algorithm of which is based on Radon (Radon) transform and fourier slice theorem, although an analysis method of which is fast, the noise immunity is poor, noise in original data is large, data is relatively undersampled, and a satisfactory reconstructed image is difficult to obtain.
Iterative reconstruction algorithms include Maximum Likelihood (MLEM), ordered subset maximum likelihood (OSEM), algebraic Reconstruction (ART), simultaneous Iterative Reconstruction (SIRT), conjugate Gradient (CGM), weighted Least Squares (WLS), maximum A Posteriori (MAP), etc. MLEM algorithms since the inverse problem of solving the emission distribution from the measurement data is an ill-defined problem, an iterative expectation-maximization algorithm that seeks a maximum likelihood solution can result in increased noise once the iteration reaches a certain point. The MAP algorithm, while eliminating divergence at higher iterations, the traditional smoothing priors or total variation previously resulted in excessive smoothing or artifacts in the reconstructed image.
The existing Positron Emission Tomography (PET) reconstruction method based on the automatic encoder network has the problems of high noise, excessive smoothness and artifacts.
How to design a Positron Emission Tomography (PET) reconstruction method based on an automatic encoder network to solve the problems proposed in the background art.
Disclosure of Invention
In view of the above-mentioned problems, the present invention aims to provide a Positron Emission Tomography (PET) reconstruction method based on an automatic encoder network, which is practical, excellent in performance and strong in environmental adaptability.
In order to achieve the purpose, the invention provides the following technical scheme: a Positron Emission Tomography (PET) reconstruction method based on an automatic encoder network comprises the following steps:
step A: establishing a Denoising Automatic Encoder (DAE) network model on the basis of a positron emission computed tomography (PET) image, and acquiring prior information of the image by using a trained Denoising Automatic Encoder (DAE);
PET reconstruction image mathematical model: measurement data y ∈ R M×1 Can be modeled as a set of independent Poisson random variables, transformed by affineAnd unknown image x ∈ R N×1 The relationship of (a) to (b) is as follows:
wherein P ∈ R M×N Is a detection probability matrix, P ij Representing the probability of a photon originating from voxel j being detected by detector i, s ∈ R M×1 And R ∈ R M×1 Respectively representing scatter and random coincidence data, M is the number of lines of response (LOR), N is the number of pixels in image space, and the log-likelihood function is:
the maximum likelihood estimate of the unknown image x is:
and B, step B: combining a Denoising Automatic Encoder (DAE) network with image prior information with a traditional PET iterative reconstruction method, and alternately iterating the Denoising Automatic Encoder (DAE) network and the traditional PET iterative reconstruction method to obtain a reconstructed image.
Further, the step a specifically includes:
(1) The method comprises the following specific steps of establishing a DAE network model:
the DAE network consists of 20 convolution layers, wherein batch normalization is carried out between the layers except the 1 st layer and the 20 th layer, except the 20 th layer, the activation is carried out by using a linear rectification function (ReLU), the size of a convolution kernel is 3 multiplied by 3, the number of input and output channels is 3 (RGB), and the number of the other layers is 64;
the output of the optimal DAE network is the local mean of the true data density, and the denoised auto-encoder (DAE) error (the difference between the output and the input of the trained auto-encoder) is the average shift vector, the size of this average shift vector is used as the negative log-likelihood of the image prior, for image reconstruction, the probability of using the gradient descent is maximized by back-propagating the auto-encoder error, a ση (I) Representing the DAE network, the input image is I, the output of the DAE network is A ση (I),The DAE is trained by minimizing a cost function:
wherein the Gaussian noise η has a varianceA ση Indicating DAE as noise varianceTraining, noise varianceAnd the degraded noise and its varianceIrrelevant, it is a specified parameter;
(2) Obtaining prior information of an image by using a DAE network, wherein L (I) = | | | A ση (I)-I|| 2 Measuring image I and local average value A thereof in true data density ση (I) The proximity of (a).
Further, the step B specifically includes:
(1) In the step B, the conventional iterative reconstruction method takes a maximum likelihood method (MLEM) as an example, and the corresponding steps are as follows:
and E: get the desired X by ML, construct alternate iterations:
and step M: will find Z ij Carry-in, let the partial derivative equal 0:
(2) Combining a Denoising Automatic Encoder (DAE) network with image prior information and an MLEM reconstruction method, and alternately iterating the two methods to obtain a reconstructed image;
wherein P ∈ R M×N Is a detection probability matrix, x is an unknown image, and gamma is a relative influence used for weighting the data item and the prior information; the DAE network iteration process is as follows: the first step is as follows: computing data items relative to an imageA gradient of (a); the second step is that: calculating the gradient of prior information, and averaging the moving vector | | | A ση (I)-I|| 2 The gradient of (A) is required fromDynamic encoder A ση (I) The gradient of (c), back-propagating the computation through the network; the final step updates the image I using a weighted sum of the two gradient terms.
Compared with the prior art, the invention has the beneficial effects that:
the invention integrates a de-noising automatic encoder (DAE) network on the basis of a positron emission computed tomography (PET) reconstruction method, unsupervised learning of prior information of a PET image is carried out by adopting the de-noising automatic encoder (DAE) network, then the DAE network with the image prior information is combined with a traditional PET iterative reconstruction method, and the two are alternately iterated to obtain a reconstructed image, thereby achieving good reconstruction effect.
Drawings
FIG. 1 is a flow chart of the present invention;
FIG. 2 is a diagram of a neural network framework constructed in accordance with the present invention;
FIG. 3 is a flowchart of a loop through the algorithmic process of the present invention;
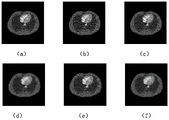
FIG. 4 is a diagram of a test apparatus according to the present invention; (a) is a true emission image; (b) is an attenuation map; (c) is the sum of the mask and the true emission image; (d) a noise-free projection data map; (e) a noisy projection data map; (f) reconstructing an image for the FBP;
FIG. 5 is a graph of results of a conventional iterative algorithm; (a) is a result graph of a traditional MLEM algorithm; (b) is a result graph of a traditional OSEM algorithm; (c) is a result graph of the E-ML-INC-EM1 algorithm; (d) is a result graph of the E-ML-INC-EM3 algorithm; (e) is a PL-OS-EMDP algorithm result graph; (f) is a PL with point characteristics algorithm result graph;
FIG. 6 is a comparison of the results of a conventional iterative algorithm and the reconstruction of the present invention; (a) is an original image; (b) reconstructing a result graph for the traditional OSEM algorithm; (c) reconstructing a result graph by using a traditional MLEM algorithm; (d) is a reconstruction result graph of the E-ML-INC-EM-3 algorithm; (E) reconstructing a result graph by using an E-PL-OS-EMDP algorithm; (f) reconstructing a result graph according to the invention.
Detailed Description
In order to make the objects, technical solutions and advantages of the present invention more apparent, the present invention will be described in further detail below with reference to the accompanying drawings and embodiments. The embodiments described herein are only for explaining the technical solution of the present invention and are not limited to the present invention.
The invention provides a technical scheme that: a Positron Emission Tomography (PET) reconstruction method based on an automatic encoder network comprises the following steps:
step A: establishing a Denoising Automatic Encoder (DAE) network model on the basis of a positron emission computed tomography (PET) image, and acquiring prior information of the image by using a trained Denoising Automatic Encoder (DAE);
PET reconstructed image mathematical model: measurement data y ∈ R M×1 Can be modeled as a set of independent Poisson random variables, transformed by affineUnknown image x ∈ R N×1 The relationship of (a) to (b) is as follows:
wherein P ∈ R M×N Is a detection probability matrix, P ij Representing the probability of a photon originating from voxel j being detected by detector i, s ∈ R M×1 And R ∈ R M×1 Respectively representing scatter and random coincidence data, M is the number of lines of response (LOR), N is the number of pixels in image space, and the log-likelihood function is:
the maximum likelihood estimate of the unknown image x is:
and B, step B: combining a Denoising Automatic Encoder (DAE) network with image prior information with a traditional PET iterative reconstruction method, and alternately iterating the Denoising Automatic Encoder (DAE) network and the traditional PET iterative reconstruction method to obtain a reconstructed image.
Further, the step a specifically includes:
(1) The method comprises the following specific steps of establishing a DAE network model:
as shown in fig. 2, the DAE network consists of 20 convolutional layers, with the exception of layer 1 and layer 20, between which batch normalization is performed, with the exception of layer 20, activation using a linear rectification function (ReLU), the size of the convolutional kernel being 3 × 3, the number of input and output channels being 3 (RGB), and the remaining layers being 64;
the output of the optimal DAE network is the local mean of the true data density, and the denoised auto-encoder (DAE) error (the difference between the output and the input of the trained auto-encoder) is the average shift vector, the size of this average shift vector is used as the negative log-likelihood of the image prior, for image reconstruction, the probability of using the gradient descent is maximized by back-propagating the auto-encoder error, a ση (I) Representing the DAE network, the input image is I, the output of the DAE network is A ση (I),The DAE is trained by minimizing a cost function:
wherein the Gaussian noise η has a varianceA ση Indicating DAE as noise varianceTraining, noise varianceAnd the variance of the degraded noiseIrrelevant, it is a specified parameter;
(2) Obtaining prior information of an image by using a DAE network, wherein L (I) = | | | A ση (I)-I|| 2 Measuring image I and local average value A thereof in true data density ση (I) The proximity of (a).
Further, the step B specifically includes:
(1) In the step B, the conventional iterative reconstruction method takes a maximum likelihood method (MLEM) as an example, and the corresponding steps are as follows:
and E: get the desired X through ML, construct alternate iterations:
and step M: will find Z ij Carry-in, let the partial derivative equal 0:
(2) Combining a Denoising Automatic Encoder (DAE) network with image prior information and an MLEM reconstruction method, and alternately iterating the two methods to obtain a reconstructed image;
wherein P ∈ R MxN Is a detection probability matrix, x is an unknown image, and gamma is a relative influence used for weighting the data item and the prior information; the DAE network iteration process is as follows: the first step is as follows: computing data items relative to an imageA gradient of (a); the second step: calculating the gradient of prior information, and averaging the moving vector | | | A ση (I)-I|| 2 The gradient of (2) requires an automatic encoder A ση (I) The gradient of (c), back-propagating the computation through the network; the last step uses two laddersThe weighted sum of the degree terms updates the image I.
| Algorithm | PSNR | SSIM |
| Traditional-FBP | 24.4681 | 0.6755 |
| Traditional-OSEM | 22.6343 | 0.7961 |
| Traditional-MLEM | 24.8795 | 0.8320 |
| E-ML-INC-EM-1 | 25.3645 | 0.8225 |
| E-PL-OS-EMDP | 21.8457 | 0.7873 |
| The invention | 30.3197 | 0.9275 |
The experimental results in the table show that the two indexes of the peak signal-to-noise ratio (PSNR) and the Structural Similarity (SSIM) of the image reconstructed by the optimized algorithm are higher than those of the image reconstructed by the traditional algorithm, so that a satisfactory effect is achieved.
The foregoing merely represents preferred embodiments of the invention, which are described in some detail and detail, and therefore should not be construed as limiting the scope of the invention. It should be noted that, for those skilled in the art, various changes, modifications and substitutions can be made without departing from the spirit of the present invention, and these are all within the scope of the present invention. Therefore, the protection scope of the present patent should be subject to the appended claims.
Claims (1)
1. A Positron Emission Tomography (PET) reconstruction method based on an automatic encoder network is characterized by comprising the following steps: the method comprises the following steps:
step A: establishing a Denoising Automatic Encoder (DAE) network model on the basis of a Positron Emission Tomography (PET) image, and acquiring prior information of the image by using a trained Denoising Automatic Encoder (DAE);
PET reconstructed image mathematical model: measurement dataCan be modeled as a set of independent Poisson random variables, transformed by affineAnd unknown imagesThe relationship of (a) to (b) is as follows:
wherein,is a matrix of the probability of detection,is represented by a detectorDetecting origin of voxelsThe probability of a photon of (a) is,andrespectively representing scatter coincidence and random coincidence data,is the number of lines of response (LOR),is the number of pixels in image space, and the log-likelihood function is:
and B: combining a Denoising Automatic Encoder (DAE) network with image prior information with a traditional PET iterative reconstruction method, and alternately iterating the Denoising Automatic Encoder (DAE) network and the traditional PET iterative reconstruction method to obtain a reconstructed image;
the step A specifically comprises the following steps:
(1) The method comprises the following specific steps of establishing a DAE network model:
the DAE network consists of 20 convolutional layers, with the exception of layer 1 and layer 20, between which batch normalization is performed, with the exception of layer 20, which is activated using a linear rectification function (ReLU), with the size of the convolutional kernel beingThe number of input and output channels is 3 (RGB), and the remaining layers are 64;
the output of the optimal DAE network is the local mean of the true data density and the denoised auto-encoder (DAE) error is the mean shift vector, the size of this mean shift vector is used as the negative log-likelihood of the image prior, for image reconstruction, the probability of using the gradient descent is maximized by back-propagating the auto-encoder error,representing a DAE network, the input image is I, the output of the DAE network is,Then the DAE is trained by minimizing a cost function:
wherein, gaussian noiseHaving a variance,Indicating DAE as noise varianceTraining, noise varianceAnd the variance of the degraded noiseIrrelevant, it is a specified parameter;
(2) Obtaining a priori information about the image using the DAE networkMeasuring image I and its local average value in real data densityThe proximity of (a);
the step B specifically comprises the following steps:
(1) In the step B, the conventional iterative reconstruction method takes a maximum likelihood method (MLEM) as an example, and the corresponding steps are as follows:
and E: get the desired X through ML, construct alternate iterations:
(2) Combining a Denoising Automatic Encoder (DAE) network with image prior information and an MLEM reconstruction method, and alternately iterating the two methods to obtain a reconstructed image;
wherein,is a matrix of the probability of detection,in order to be an unknown image,is used to weight the relative influence of the data item and the prior information; the DAE network iteration process is as follows: the first step is as follows: computing data items against an imageA gradient of (a); second step, calculating the gradient of prior information and averaging the moving vectorGradient of (2) requires an automatic encoderThe gradient of (c), back-propagating the computation through the network; the final step updates the image I using a weighted sum of the two gradient terms.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201811247856.3A CN109584324B (en) | 2018-10-24 | 2018-10-24 | Positron Emission Tomography (PET) reconstruction method based on automatic encoder network |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201811247856.3A CN109584324B (en) | 2018-10-24 | 2018-10-24 | Positron Emission Tomography (PET) reconstruction method based on automatic encoder network |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN109584324A CN109584324A (en) | 2019-04-05 |
| CN109584324B true CN109584324B (en) | 2022-12-06 |
Family
ID=65920560
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN201811247856.3A Active CN109584324B (en) | 2018-10-24 | 2018-10-24 | Positron Emission Tomography (PET) reconstruction method based on automatic encoder network |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN109584324B (en) |
Families Citing this family (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN110246094B (en) * | 2019-05-13 | 2021-09-28 | 南昌大学 | 6-dimensional embedded denoising self-coding prior information algorithm for color image super-resolution reconstruction |
| CN111627082B (en) * | 2020-05-21 | 2022-06-21 | 浙江大学 | PET image reconstruction method based on filtering back projection algorithm and neural network |
| CN111709897B (en) * | 2020-06-18 | 2023-10-24 | 深圳先进技术研究院 | Domain transformation-based positron emission tomography image reconstruction method |
| WO2021253326A1 (en) * | 2020-06-18 | 2021-12-23 | 深圳先进技术研究院 | Domain transform-based method for reconstructing positron emission tomography image |
| CN112258414B (en) * | 2020-10-26 | 2023-11-10 | 北京航星机器制造有限公司 | Noise suppression method for security inspection CT ray signals |
| CN112862915B (en) * | 2021-03-02 | 2024-05-28 | 明峰医疗系统股份有限公司 | PET image reconstruction method, system and computer readable storage medium based on non-training neural network |
| CN113469915A (en) * | 2021-07-08 | 2021-10-01 | 深圳高性能医疗器械国家研究院有限公司 | PET reconstruction method based on denoising and scoring matching network |
| CN114332287B (en) * | 2022-03-11 | 2022-07-15 | 之江实验室 | Method, device, equipment and medium for reconstructing PET (positron emission tomography) image based on transformer feature sharing |
Citations (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN105573121A (en) * | 2016-01-18 | 2016-05-11 | 南昌大学 | Autonomous adjusting deadweight balance mechanism control algorithm for force feedback equipment |
Family Cites Families (6)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CA2495215A1 (en) * | 2002-08-12 | 2004-02-19 | Naviscan Pet Systems, Inc. | Mission-specific positron emission tomography |
| CN105678821B (en) * | 2016-01-12 | 2018-08-07 | 浙江大学 | A kind of dynamic PET images method for reconstructing based on self-encoding encoder image co-registration |
| CN109863512B (en) * | 2016-09-01 | 2023-10-20 | 通用医疗公司 | System and method for automatic transformation by manifold approximation |
| US10074038B2 (en) * | 2016-11-23 | 2018-09-11 | General Electric Company | Deep learning medical systems and methods for image reconstruction and quality evaluation |
| WO2018106805A1 (en) * | 2016-12-09 | 2018-06-14 | William Marsh Rice University | Signal recovery via deep convolutional networks |
| US10475214B2 (en) * | 2017-04-05 | 2019-11-12 | General Electric Company | Tomographic reconstruction based on deep learning |
-
2018
- 2018-10-24 CN CN201811247856.3A patent/CN109584324B/en active Active
Patent Citations (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN105573121A (en) * | 2016-01-18 | 2016-05-11 | 南昌大学 | Autonomous adjusting deadweight balance mechanism control algorithm for force feedback equipment |
Also Published As
| Publication number | Publication date |
|---|---|
| CN109584324A (en) | 2019-04-05 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN109584324B (en) | Positron Emission Tomography (PET) reconstruction method based on automatic encoder network | |
| EP2156408B1 (en) | Pet local tomography | |
| CN102831627A (en) | PET (positron emission tomography) image reconstruction method based on GPU (graphics processing unit) multi-core parallel processing | |
| CN106846427B (en) | A kind of limited angle CT method for reconstructing based on the weighting full variation of anisotropy again | |
| CN102184559B (en) | Particle filtering-based method of reconstructing static PET (Positron Emission Tomograph) images | |
| CN109712213B (en) | PET image reconstruction method, system, readable storage medium and apparatus | |
| Evangelista et al. | A new bayesian Poisson denoising algorithm based on nonlocal means and stochastic distances | |
| Liu et al. | Singular value decomposition-based 2D image reconstruction for computed tomography | |
| CN111161182A (en) | MR structure information constrained non-local mean guided PET image partial volume correction method | |
| Zhang et al. | Weighted tensor low-rankness and learnable analysis sparse representation model for texture preserving low-dose CT reconstruction | |
| Huang et al. | Gapfill-recon net: a cascade network for simultaneously pet gap filling and image reconstruction | |
| Nuyts | On estimating the variance of smoothed MLEM images | |
| WO2011100575A2 (en) | Systems, methods and computer readable storage mediums storing instructions for applying multiscale bilateral filtering to magnetic resonance (mr) images | |
| Pfister | Tomographic reconstruction with adaptive sparsifying transforms | |
| Lee et al. | A modified OSEM algorithm for PET reconstruction using wavelet processing | |
| Kamasak et al. | Quality and precision of parametric images created from PET sinogram data by direct reconstruction: proof of concept | |
| Song et al. | 4D reconstruction of cardiac SPECT using a robust spatialtemporal prior | |
| Rajith et al. | Edge preserved de-noising method for medical x-ray images using wavelet packet transformation | |
| Li et al. | Robust frame based X-ray CT reconstruction | |
| Gopi et al. | Iterative computed tomography reconstruction from sparse-view data | |
| Boudjelal et al. | PDEs on graphs for image reconstruction on positron emission tomography | |
| Gopi et al. | Regularization based CT image reconstruction using Algebraic techniques | |
| Bai et al. | PET image reconstruction: methodology and quantitative accuracy | |
| US20190206094A1 (en) | Fast iterative image reconstruction method for emission tomography | |
| Kaur et al. | Complex diffusion regularisation-based low dose CT image reconstruction |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |