ഫൗക്കോൾ പെൻഡുലം

ഇംഗ്ലീഷ് വിലാസം

https://ml.wikipedia.org/wiki/Foucault_pendulum

പാരിസിലെ പാന്തിയോണിൽ പ്രദർശിപ്പിച്ചിട്ടുള്ള ഫൗക്കോൾ പെൻഡുലം.

Foucault Pendulum at COSI Columbus knocking over a ball

ഫൗക്കോൾ പെൻഡുലം (English: /fuːˈkoʊ/ foo-KOH; French pronunciation: ​[fuˈko]) അല്ലെങ്കിൽ ഫൗക്കോളിന്റെ പെൻഡുലം എന്നറിയപ്പെടുന്നത് ഒരു ലഘുവായ ഉപകരണമാണ്. ഇത് ഫ്രഞ്ച് ഭൗതികശാസ്ത്രജ്ഞനായ ലിയോൺ ഫൗക്കോളിന്റെ പേരിലാണ് അറിയപ്പെടുന്നത്. ഭൂമിയുടെ കറക്കം തെളിയിക്കുന്ന ഒരു ലളിതമായ പരീക്ഷണമാണിത്. 1851 ലാണ് ഈ പെൻഡുലം ഉണ്ടാക്കിയത്. ഭൂമിയുടെ ഭ്രമണത്തിന്റെ ലളിതമായ, നേരിട്ടുള്ള തെളിവുകൾ നൽകുന്ന ആദ്യ പരീക്ഷണമായിരുന്നു അത്. ഇന്ന്, മ്യൂസിയങ്ങളിലും സർവ്വകലാശാലകളിലും ഫൗക്കോൾ പെൻഡുലങ്ങൾ പ്രമുഖ പ്രദർശനവസ്തുക്കളാണ്.

യഥാർത്ഥ ഫൗക്കോൾ പെൻഡുലം

പാരീസിലെ പാന്തിയോണിലുള്ള ഫൗക്കോൾ പെൻഡുലം

1895 ലെ ഫൂക്കോൾ പെൻഡുലത്തിന്റെ വരപ്പ്

1851 ഫെബ്രുവരിയിൽ, പാരിസ് ഒബ്സർവേറ്ററിയിലെ മെരിഡിയനിൽ ഒരു ഫൗക്കോൾ പെൻഡുലം ആദ്യത്തെ പൊതു പ്രദർശനം നടന്നു.  ഏതാനും ആഴ്ചകൾക്കു ശേഷം, ഫാകോൾട്ട് തന്റെ ഏറ്റവും പ്രശസ്തമായ പെൻഡുലം ഉണ്ടാക്കി, 28 കിലോഗ്രാം ഭാരമുള്ള ചെമ്പ് പൂശിയ ബോബ് 67 മീറ്റർ നീളമുള്ള ഒരു വയറിൽ പാരീസിലെ പാന്തിയോണിലെ ഡോമിൽ നിന്ന് കെട്ടിത്തൂക്കിയാണ് ഇത് നിർമ്മിച്ചത്. ഒരുമണിക്കൂറിൽ 11.3° ക്ലോക്ക് ദിശയിൽ  പെൻഡുലത്തിന്റെ പ്രതലം തിരിയുന്നു. 31.8 മണിക്കൂറുകൾകൊണ്ട് പ്രതലം ഒരു പൂർണ്ണ തിരിച്ചിൽ പൂർത്തിയാക്കുന്നു. 1851 ൽ പാന്തിയോണിൽ ഉപയോഗിച്ച യഥാർത്ഥ ബോബ് 1855 ൽ കൺസെർവാറ്റിയോറെ ഡെ ആർട്സ് എറ്റ് മെറ്റിയേർസിലേക്ക് മാറ്റി. 50-ാം വാർഷികമായ 1902 ൽ ഒരു താത്കാലിക പെൻഡുലം സ്ഥാപിച്ചു.

1990കളിൽ മ്യൂസിയത്തിന്റെ പുനർനിർമ്മാണവേളയിൽ യഥാർത്ഥ പെൻഡുലം പാന്തിയോണിലേക്ക് മാറ്റി (1995 ൽ). 2000 ൽ മ്യൂസീ ഡെസ് ആർട്സ് എറ്റ് മെറ്റിയേർസ് വീണ്ടും തുറക്കുന്നതിനുമുൻപേ ഇത് തിരിച്ചുകൊണ്ടുപോയി. 6 ഏപ്രിൽ 2010 ൽ ബോബ് തൂക്കിയിട്ടിരുന്ന വള്ളിപൊട്ടി താഴെവീണു. ഇത് ബോബിലും മ്യൂസിയത്തിന്റെ തറയ്ക്കും പരിഹരിക്കാൻ പറ്റാത്ത കേടുപാടുണ്ടാക്കി.

1995 മുതൽ പാന്തിയോണിൽ ഈ പെൻഡുലത്തിന്റെ യഥാർത്ഥ പകർപ്പ് പ്രവർത്തിക്കുന്നുണ്ട്.

മെക്കാനിക്സിന്റെ വിശദീകരണം

Animation of a Foucault pendulum at the Pantheon in Paris (48° 52' north), with the Earth's rotation rate greatly exaggerated. The green trace shows the path of the pendulum bob over the ground (a rotating reference frame), while in any vertical plane. The actual plane of swing appears to rotate relative to the Earth. The wire should be as long as possible—lengths of 12–30 മീ (39–98 അടി) are common.

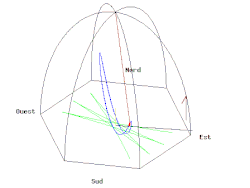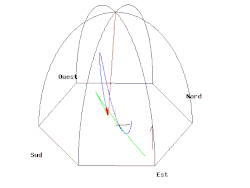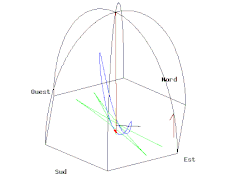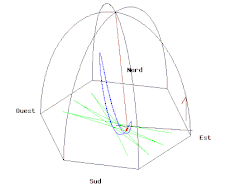
ഉത്തരധ്രുവത്തിലും ദക്ഷിണധ്രുവത്തിലും പെൻഡുലത്തിന്റെ ദോലന പ്രതലം ഭൂമിയിൽനിന്നും വളരെ അകലെയുള്ള വസ്തുക്കളെ അപേക്ഷിച്ച് സ്ഥിരമായിരിക്കും, എന്നാൽ പ്രതലത്തിനു താഴെയുള്ള ഭൂമി കറങ്ങിക്കൊണ്ടിരിക്കും. ഒരു കറക്കം പൂർത്തിയാക്കാൻ ഒരു ഖഗോള ദിനം എടുക്കും. അതുകൊണ്ട് ഭൂമിയെ അപേക്ഷിച്ച് ഉത്തരധ്രുവത്തിലുള്ള പെൻഡുലത്തിന്റെ ദോലന പ്രതലം ഒരു ദിവസം കൊണ്ട് ഒരു പൂർണ്ണ കറക്കം ഘടികാരദിശയിൽ പൂർത്തിയാക്കും. ദക്ഷിണ ധ്രുവത്തിൽ ഇത് എതിർ ഘടികാരദിശയിലായിരിക്കും.

ഭൂമദ്ധ്യരേഖയിൽ ഉള്ള ഫൗക്കോൾ പെൻഡുലത്തിന്റെ ദോലന പ്രതലം ഭൂമിയെ അപേക്ഷിച്ച് സ്ഥിരമായിരിക്കും. മറ്റ് അക്ഷാംശങ്ങൾ ഭൂമിയേ അപേക്ഷിച്ച് മുന്നോട്ടായിരിക്കും. എന്നാൽ ധ്രുവങ്ങളിൽ കൂടുതൽ പതുക്കെയായിരിക്കും. ഇത് ω കോണീയ പ്രവേഗത്തിലായിരിക്കും. ഇത് അക്ഷാംശത്തിന്റെ സൈൻ വാല്യുവിന് അനുപാതത്തിലുമായിരിക്കും, φ:

$\omega =360^{\circ }\sin \varphi \ /\mathrm {day}$,

ഭൂമദ്ധ്യരേഖയ്ക്ക് ഉത്തര ദിശയിലേയും ദക്ഷിണദിശയിലേയും അക്ഷാംശം യഥാക്രമം ധനമായും ഋണമായും കണക്കാക്കാം. ഉദാഹരണത്തിന് 30° തെക്ക് അക്ഷാംശമുള്ള ഫൂക്കോൾ പെൻഡുലം ഭൂമിക്ക് മുകളിലുള്ള ഒരു സ്ഥലത്തുനിന്നും വീക്ഷിച്ചാൽ 360° എതിർ ഘടികാരദിശയിൽ രണ്ട്ദിവസം കൊണ്ട് തിരിയും.

A Foucault pendulum at the North Pole: The pendulum swings in the same plane as the Earth rotates beneath it.

1852 ൽ ഫൂക്കോൾ ഗൈറോസ്കോപ്പ് ഉപയോഗിച്ച് ഭൂമിയുടെ കറക്കം വ്യംഗ്യമായി അവതരിപ്പിച്ചു. ഗൈറോസ്കോപ്പിന്റെ അകത്തുള്ള ഗിബാൾ പുറത്തുള്ള ഗിംബാളിന്റെ ബെയറിംഗുകളുടെ മുനകളിൽ ബാലൻസുചെയ്തിരിക്കുന്നു. പുറത്തുള്ള ഗിംബാൾ ഒരു ടോർഷൻ വിമുക്തമായ നൂലിൽ തൂക്കിയിട്ടിരിക്കുന്നു. ഇത് താഴെയുള്ള പിവട്ട് പോയന്റിൽ ഘനം വരാത്തവിധത്തിലാണ് തൂക്കിയിട്ടിരിക്കുന്നത്.  9000-1200 കറക്കം പ്രതിമിനിട്ടിൽ വരത്തക്കവിധം ചില ഗിയറുകളുടെ സഹായത്തോടെ ഗൈറോസ്കോപ്പ് കറക്കിവിടുന്നു. അതിനുശേഷം ഇത് പരീക്ഷണത്തിനായി സ്ഥാപിക്കുന്നു. ഇത് ഏകദേശം 10 മിനിട്ടോളം പരീക്ഷണം നടത്താൻ മതിയായതാണ്.  ഈ സംവിധാനം ഒരു ഡിഗ്രിസ്കെയിലിന്റെ പത്തിലൊരംശം പോലും കാണാൻ ശേഷിയുള്ള മൈക്രോസ്കോപ്പ്  ഉപയോഗിച്ച് നിരീക്ഷിക്കുന്നു(വളരെ ദൂരെയുള്ള പോയിന്റർ ഉപയോഗിച്ചും നിരീക്ഷിക്കാം). ഫൂക്കോൾട്ട് ഗൈറോയുടെ മൂന്ന് പകർപ്പുകൾ സൃഷ്ടിക്കപ്പെട്ടിട്ടുണ്ട്. ഇവ യാത്രയിൽ കൊണ്ടുപോകാവുന്ന തരത്തിലാണ് ഉള്ളത്. യുകെയിലും ഫ്രാൻസിലും യുഎസ്സിലും ഈ പകർപ്പുകളുണ്ട്.

വളരെ ശ്രദ്ധയോടെമാത്രമേ ഫൂക്കോൾ പെൻഡുലം നിർമ്മിക്കാൻ കഴിയുകയുള്ളൂ. കൃത്യമല്ലാത്ത നിർമ്മിതി കൂടുതൽ ബലം ഉണ്ടാക്കുകയും ഇത് ടെറസ്ട്രിയൽ ഇഫക്റ്റ് ഉണ്ടാക്കാനും ഇടയുണ്ട്. പെൻഡുലത്തിന്റെ പ്രവർത്തന ആരഭം വളരെ പ്രധാനപ്പെട്ടതാണ്. സാധാരണയായി ബോബ് ഒരു നൂൽ ഉപയോഗിച്ച് കെട്ടിവയ്ക്കുകയും ആ നൂൽ കത്തിക്കുകയുമാണ് ചെയ്യുന്നത്. ഇത് വശങ്ങളിലേക്കുള്ള അനാവശ്യ ചലനങ്ങൾ ഒഴിവാക്കുന്നു.

An excerpt from the illustrated supplement of the magazine Le Petit Parisien dated November 2, 1902, on the 50th anniversary of the experiment of Léon Foucault demonstrating the rotation of the earth.

വായു പ്രതിരോധം ദോലനത്തെ പതുക്കെയാക്കുന്നു. അതുകൊണ്ട് ചില മ്യൂസിയങ്ങളിൽ ഒരു വൈദ്യുതകാന്തിക സംവിധാനമോ മറ്റ് ചില സംവിധാനങ്ങളോ ദോലനം നിന്നുപോകാതിരിക്കാൻ ഏർപ്പെടുത്തിയിട്ടുണ്ട്. ചില പെൻഡുലങ്ങൾ കൃത്യമായ ഇടവേളകളിൽ നിറുത്തി വീണ്ടും തുടങ്ങുന്നു. ചിലപ്പോൾ തുടങ്ങുന്നതിന് ഗംഭീര പരിപാടിയും ഉണ്ടാവാറുണ്ട്.

The animation describes the motion of a Foucault pendulum at a latitude of 30°N. The plane of oscillation rotates by an angle of −180° during one day, so after two days, the plane returns to its original orientation.

പെൻഡുലം സ്ഥിതിചെയ്യുന്ന സ്ഥലത്തിന് ഒരുവട്ടം പൂർണ്ണമായി തിരിഞ്ഞ് തുടങ്ങിയ സ്ഥലത്ത് എത്താനുള്ള കാലമാണ് പെൻഡുലം ദിവസം. ഇത് ഒരു ഖഗോളദിവസത്തെ ലാറ്റിറ്റ്യൂഡിന്റെ സൈൻ വിലകൊണ്ട് ഹരിച്ചുകിട്ടുന്ന വിലയാണ്.

റാഞ്ചി സയൻസ് സെന്ററിലെ ഫൂക്കോൾ പെൻഡുലം.

ബന്ധമുള്ള മറ്റ് ഭൗതിക സംവിധാനങ്ങൾ

The device described by Wheatstone.

ഒരു കറങ്ങുന്ന വസ്തുവിന്റെ മുകളറ്റത്തിന്റെ ഘൂർണ്ണനം 1836 ൽ തന്നെ സ്കോട്ടിഷ് ഗണിതജ്ഞനായ എഡ്വാർ സാങ് പറഞ്ഞിരുന്നു. 1851ൽ ചാൾസ് വീറ്റ്സ്റ്റോൺ വിറയ്ക്കുന്ന ഒരു സ്പ്രിംഗ്  ഘടന ഉൾക്കൊള്ളുന്ന ഒരു യന്ത്രം വിവരിക്കുന്നു.  ഇത് വിറയ്ക്കുന്ന ഒരു സ്പ്രിംഗ് ഒരു ഡിസ്കിന്റെ മുകളിൽ $\phi$ കോണിൽ ഉറപ്പിച്ചിരിക്കുന്നു. സ്പ്രിംഗിന് അനങ്ങാനാവാത്തതിനാൽ അത് ഒരു തലത്തിൽ തന്നെയായിരിക്കും വിറയ്ക്കുന്നത്. ഡിസ്ക് കറങ്ങുമ്പോൾ വിറയ്ക്കലിന്റെ തലം മാറുകയും ചെയ്യുന്നു. ഇത് ഫൂക്കോൾട് പെൻഡുലം$\phi$ലാറ്റിറ്റ്യൂഡിൽ വച്ചതുപോലെ പോലെ പ്രവർത്തിക്കുന്നു.

ലോകത്തിന്റെ വിവിധ ഭാഗങ്ങളിലുള്ള ഫൗക്കോൾ പെൻഡുലങ്ങൾ

The Foucault pendulum at the California Academy of Sciences knocks over successive pegs as the Earth rotates

ലോകമാകമാനം അനേകം സർവ്വകലാശാലകളിലും ശാസ്ത്രമ്യൂസിയങ്ങളിലും ഫൗക്കോൾ പെൻഡുലങ്ങൾ ഉണ്ട്. ന്യൂയോർക്കിലെ യുണൈറ്റഡ് നേഷൻസിന്റെ ആസ്ഥാനമന്ദിരത്തിലും ഉണ്ട് ഒരെണ്ണം. ഒറെഗോൺ കൺവെൻഷൻ സെന്ററിലുള്ളതാണ് ഏറ്റവും വലുത്.

ദക്ഷിണ ധ്രുവത്തിൽ

ഭൂമിയുടെ ഭ്രമണത്തിന്റെ ഫലം ഏറ്റവും കൂടുതലുള്ള ദക്ഷിണ ധ്രുവത്തിൽ ഈ പരീക്ഷണം നടത്തിയിട്ടുണ്ട്. 33 മീറ്റർ നീളമുള്ള പെൻഡുലത്തിന് 25 കിലോഗ്രാമുള്ള ബോബ് ഉണ്ടായിരുന്നു. ഇതിനായി തിരഞ്ഞെടുത്ത സ്ഥലം വളരെ നല്ലതായിരുന്നു. ഇവിടെ ചലിക്കുന്ന വായുവില്ലായിരുന്നു. തണുത്ത വായുവിന്റെ സാന്ദ്രത കുറവായത് ചലനത്തെ പ്രതിരോധിക്കുന്ന വായുമർദ്ദം കുറവായിരുന്നു. 24 മണിക്കൂറാണ് ഇതിന്റെ പരിക്രമണ കാലം എന്ന് ഗവേഷകർ സമ്മതിച്ചിട്ടുണ്ട്

ഇതും കാണുക

• കൊറിയോലിസ് ബലം
  
• Earth's rotation
• Eötvös experiment
• Inertial frame
• Absolute rotation
• ലരിയറ്റ് ചെയിൻ‎
• Precession

അധിക വായനയ്ക്ക്

• Arnold, V.I. (1989). Mathematical Methods of Classical Mechanics. Springer. p. 123. ISBN 0-387-96890-3. {{cite book}}: Invalid |ref=harv (help)
• Marion, Jerry B.; Thornton, Stephen T. (1995). Classical dynamics of particles and systems (4th ed.). Brooks Cole. pp. 398–401. ISBN 0-03-097302-3. {{cite book}}: Invalid |ref=harv (help)
• Persson, Anders O. (2005). "The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885" (PDF). History of Meteorology. 2. Archived from the original (PDF) on 2014-04-11. Retrieved 2018-09-07. {{cite journal}}: Invalid |ref=harv (help)

പുറത്തേക്കുള്ള കണ്ണികൾ

• Rubin, Julian (2007). "The Invention of the Foucault Pendulum". Following the Path of Discovery, 2007, retrieved 2007-10-31. Directions for repeating Foucault's experiment, on amateur science site.
• Wolfe, Joe, "A derivation of the precession of the Foucault pendulum".
• "The Foucault Pendulum", derivation of the precession in polar coordinates.
• "The Foucault Pendulum" By Joe Wolfe, with film clip and animations.
• "Foucault's Pendulum" by Jens-Peer Kuska with Jeff Bryant, Wolfram Demonstrations Project: a computer model of the pendulum allowing manipulation of pendulum frequency, Earth rotation frequency, latitude, and time.
• "Webcam Kirchhoff-Institut für Physik, Universität Heidelberg".
• California academy of sciences, CA Archived 2016-05-25 at the Portugese Web Archive Foucault pendulum explanation, in friendly format
• Foucault pendulum model Exposition including a tabletop device that shows the Foucault effect in seconds.
• Foucault, M. L., Physical demonstration of the rotation of the Earth by means of the pendulum, Franklin Institute, 2000, retrieved 2007-10-31. Translation of his paper on Foucault pendulum.
• Tobin, William. "The Life and Science of Léon Foucault". Archived from the original on 2018-09-12. Retrieved 2018-09-07.
• Bowley, Roger (2010). "Foucault's Pendulum". Sixty Symbols. Brady Haran for University of Nottingham.
• Foucault-inga Párizsban Foucault's Pendulum in Paris – video of the operating Foucault's Pendulum in the Panthéon (ഹംഗേറിയൻ).
• Pendolo nel Salone The Foucault Pendulum inside Palazzo della Ragione in Padova, Italy
• MacMillan, William Duncan (1915). "On Foucault's Pendulum". Am. J. Math. 37 (1): 95–106. doi:10.2307/2370259.
• Somerville, W. B. (1972). "The description of Foucault's pendulum". Q. Jl. R. astr. Soc. 13: 40–62. Bibcode:1972QJRAS..13...40S.
• Braginsky, Vladimir B.; Polnarev, Aleksander G.; Thorne, Kip S. (1984). "Foucault Pendulum at the South Pole: Proposal For an Experiment to Detect the Earth's General Relativistic Gravitomagnetic Field". Phys. Rev. Lett. 53: 863. Bibcode:1984PhRvL..53..863B. doi:10.1103/PhysRevLett.53.863.
• Crane, H. Richard (1995). "Foucault pendulum "wall clock"". Am. J. Phys. 63: 33. Bibcode:1995AmJPh..63...33C. doi:10.1119/1.17765.
• Hard, John B.; Miller, Raymond E. (1998). "A simple geometric model for visualizing the motion of a Foucault pendulum". Am. J. Phys. 55 (1): 67. doi:10.119/1.14972. {{cite journal}}: Check |doi= value (help)
• Das, U.; Talukdar, B.; Shamanna, J. (2002). "Indirect Analytic Representation of Foucault's Pendulum". Czech. J. Phys. 52 (12): 1321–1327. Bibcode:2002CzJPh..52.1321D. doi:10.1023/A:1021819627736.
• Salva, Horacio R.; Benavides, Robén E.; Perez, Julio C.; Cuscueta, Diego J. (2010). "A Foucault's pendulum design". Rev. Sci. Instrum. 81: 115102. Bibcode:2010RScI...81k5102S. doi:10.1063/1.3494611.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Daliga, K.; Przyborski, M.; Szulwic, J. (2015). "Foucault's Pendulum. Uncomplicated Tool in the Study of Geodesy and Cartography". ISBN 978-84-606-8243-1. {{cite journal}}: Cite journal requires |journal= (help), EDULEARN15 Proceedings - 7th International Conference on Education and New Learning Technologies, Barcelona, Spain