Gruppen
(318) Eine Gruppe ist eine Menge, auf der nur eine Verknüpfung definiert ist.
Das kann z.B. eine Addition oder
Multiplikation oder die Hintereinanderausführung von Drehungen einer Ebene
um einen festen Punkt sein. Wir benutzen daher ein neues Zeichen  für die Verknüpfung in einer Gruppe.
für die Verknüpfung in einer Gruppe.
Definition.
Eine Menge 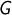 heißt Gruppe, falls auf
heißt Gruppe, falls auf 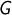 eine
Verknüpfung
eine
Verknüpfung
definiert ist derart, dass die folgenden Regeln gelten:
 für alle
für alle  ,
so heißt
,
so heißt 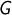 abelsch oder
kommutativ. Eine Abbildung
abelsch oder
kommutativ. Eine Abbildung  einer Gruppe
einer Gruppe 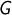 mit Verknüpfung
mit Verknüpfung  in eine Gruppe
in eine Gruppe  mit
Verknüpfung
mit
Verknüpfung  heißt
Homomorphismus, wenn
heißt
Homomorphismus, wenn
 für alle
für alle  gilt.
gilt.
- (G1)
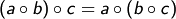 für alle
für alle  (Assoziativgesetz)
(Assoziativgesetz)
- (G2) Es gibt ein neutrales Element
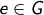 so, dass
so, dass  für alle
für alle  gilt. Man nennt
gilt. Man nennt 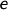 auch linksneutral.
auch linksneutral.
- (G3) Zu jedem
 gibt es ein inverses Element
gibt es ein inverses Element  so, dass
so, dass  gilt. Man nennt
gilt. Man nennt  auch
Linksinverses zu
auch
Linksinverses zu  .
.
Beispiele.
Jeder Körper ist bezüglich Addition eine abelsche
Gruppe. Neutrales Element ist 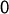 , und
, und 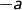 ist invers zu
ist invers zu  .
.
Ist ein Körper, so ist
ein Körper, so ist
 bezüglich Multiplikation eine abelsche Gruppe mit neutralem Element
bezüglich Multiplikation eine abelsche Gruppe mit neutralem Element  .
.
Ist
Wir kommen nun zu einem ersten mathematischen Beweis. Wir zeigen,
dass in einer Gruppe 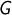 jedes neutrale Element auch rechtsneutral ist
und dass alle zu
jedes neutrale Element auch rechtsneutral ist
und dass alle zu  inversen Elemente auch Rechtsinverse zu
inversen Elemente auch Rechtsinverse zu  sind. Daraus ergibt sich dann, dass es überhaupt nur ein neutrales Element
in einer Gruppe gibt und dass auch das inverse Element eindeutig bestimmt
ist.
sind. Daraus ergibt sich dann, dass es überhaupt nur ein neutrales Element
in einer Gruppe gibt und dass auch das inverse Element eindeutig bestimmt
ist.
Satz.
Sei 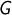 eine Gruppe mit neutralem Element
eine Gruppe mit neutralem Element 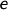 . Dann gelten:
. Dann gelten:
-
 und
und  für alle
für alle 
- Es gibt genau ein
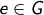 mit
mit  ,
und zu jedem
,
und zu jedem  gibt es genau ein inverses Element
gibt es genau ein inverses Element  mit
mit

Beweis.
- Sei
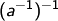 ein Inverses von
ein Inverses von  . Dann folgt
. Dann folgt

Hieraus folgt und damit Teil 1.
und damit Teil 1.
- Seien
 mit
mit  , dann gilt
, dann gilt
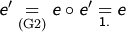
Ist , dann folgt
, dann folgt
