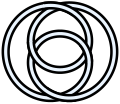
Nodo a otto

In matematica, e più precisamente in teoria dei nodi, il nodo a otto (o figura otto, espressione tradotta letteralmente dall'inglese) è il nodo più semplice dopo il nodo trifoglio.
Il nodo a otto ha avuto un ruolo determinante nello studio delle varietà tridimensionali alla fine degli anni settanta, quando il matematico William Thurston costruì una struttura di spazio iperbolico sul suo complementare.
Il nome del nodo è derivato dalla nomenclatura adottata per i nodi otto e otto ripassato, usati nell'alpinismo.
Definizione

Il nodo a otto può essere descritto dalla curva nello spazio
Il nodo è l'unico raffigurabile con un diagramma con 4 incroci, ma non con un numero minore di incroci.
Proprietà
Il nodo a otto presenta molte differenze con il nodo a trifoglio:
- non è un nodo torico;
- sul suo complementare (nella sfera ) è possibile assegnare una metrica che lo rende uno spazio iperbolico;
- non è chirale: l'immagine riflessa del nodo figura a otto è equivalente al nodo stesso.
Grazie al nodo figura a otto, e agli importanti lavori di William Thurston[1], è stato possibile costruire una infinità di varietà iperboliche tridimensionali. Molti nodi hanno il complementare iperbolico: il complementare del nodo figura a otto è, fra questi, quello con volume minore, pari a 2.02988...[2]. Il complementare del nodo si intende sempre nella sfera tridimensionale , ottenuta aggiungendo il "punto all'infinito" allo spazio tridimensionale .
In altre forme:
Note
- ^ (EN) William Thurston, The Geometry and Topology of Three-Manifolds, Princeton University lecture notes (1978-1981).
- ^ (EN) Chun Cao and Robert Meyerhoff, The orientable cusped hyperbolic 3-manifolds of minimum volume, Inventiones Mathematicae, 146 (2001), no. 3, 451--478.
Voci correlate
Altri progetti
 Wikimedia Commons contiene immagini o altri file sul nodo a otto
Wikimedia Commons contiene immagini o altri file sul nodo a otto
Collegamenti esterni
- (EN) Eric W. Weisstein, Nodo a otto, su MathWorld, Wolfram Research.
![{\displaystyle f:[0,2\pi ]\to \mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af770f6564d10d72ec962626e4e39a47dd9c3639)