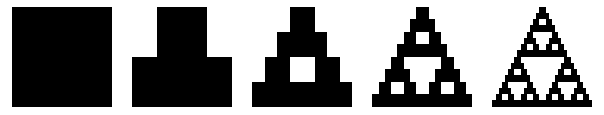Triángulo de Sierpinski

O Triángulo de Sierpinski é unha figura xeométrica obtida a través dun proceso recursivo. É unha das formas elementais da xeometría fractal por presentar propiedades tales como ter tantos puntos como o do conxunto dos números reais, ter área igual a cero, ser auto-semellante (unha súa parte é idéntica en total), non perder a súa definición inicial á medida que se amplía.
Foi primeiramente descrito por Waclaw Sierpinski (1882 - 1969), matemático polonés
Construción
[editar | editar a fonte]Unha das maneiras de obter un triángulo de Sierpinski é a través do seguinte algoritmo:
- Comece con calquera triángulo nun plano. O triángulo de Sierpinski canónico utilizaba un triángulo equilátero coa base paralela ao eixo horizontal, mais calquera triángulo pode usarse (ver primeira figura).
- Encolla o triángulo pola metade (cada lado debe ter metade do tamaño orixinal), faga tres copias, e posicione cada triángulo de maneira que se achegue aos outros dous nun canto (ver segunda figura).
- Repita o paso 2 para cada figura obtida, indefinidamente (ver a partir da terceira figura).
Aínda que no proceso enriba a figura inicial sexa un triángulo, non é necesario partir dun para se chegar no triángulo de Sierpinski. É posíbel utilizar calquera figura xeométrica (ver abaixo), o triángulo só utilízase por facilitar a visualisación.
O fractal propiamente dito obtense ao repitir infinitas veces o proceso do algoritmo, mais conforme o número de iteracións aumenta, a imaxe obtida tende a se tornar cada vez máis parecida co fractal.
Propiedades
[editar | editar a fonte]O triángulo de Sierpinski posúe unha dimensión de Hausdorff de aproximadamente 1,585 (log(3)/log(2)). Iso acontece porque esa é unha figura formada por tres copias de si mesma, cada unha reducida por un factor de 1/2.
Tamén existe unha relación co triángulo de Pascal. Montando o triángulo de Pascal con 2n liñas, e pintando os números pares de branco e os ímpares de negro, a figura obtida será unha aproximación do triángulo de Sierpinski.
A área dun triángulo de Sierpinski é cero. Iso pode ser percibido cando observamos que, a cada iteración, a área da figura obtida foi reducida en 25% en relación a área da figura orixinal.