打开本页,如果不能显示公式,请刷新浏览器。
$$\mathbb{V}$$ 和 $$\mathbb{W}$$ 是两个向量空间,有线性变换 $$\pmb{T}:\mathbb{V}\to\mathbb{W}$$ ,将输入向量 $$\pmb{x}\in\mathbb{V}$$ 映射到输出向量 $$\pmb{T}(\pmb{x})\in\mathbb{W}$$ 。
对于任意 $$\pmb{x,y}\in\mathbb{V}$$ 和标量 $$c$$ ,线性变换 $$\pmb{T}$$ 满足下列性质:
$$\begin{split}\pmb{T}(\pmb{x}+\pmb{y})&=\pmb{T}(\pmb{x})+\pmb{T}(\pmb{y})\\pmb{T}(c\pmb{x})&=c\pmb{T}(\pmb{x})\end{split} \tag{1}$$
若 $$\mathbb{V}=\mathbb{W}$$ 也称 $$\pmb{T}$$ 为线性算子(算符)。
假设几何向量空间 $$\mathbb{R}^2$$ ,任一线性算子 $$\pmb{T}:\mathbb{R}^2\to\mathbb{R}^2$$ 都可以用 $$2\times 2$$ 实数矩阵 $$\pmb{A}$$ 表示:
$$\pmb{T}(\pmb{x})=\pmb{Ax}\tag{2}$$
其中 $$\pmb{x}\in\mathbb{R}^2$$ 。称 $$\pmb{A}$$ 是线性算子 $$\pmb{T}$$ 的变换矩阵或表示矩阵。
下面研究在二维几何空间的镜像反射变换(reflection)。对于向量 $$\pmb{x}=\begin{bmatrix}x_1\x_2\end{bmatrix}$$ ,以x轴为镜面的反射变换:
$$\pmb{T}\left(\begin{bmatrix}x_1\x_2\end{bmatrix}\right)=\begin{bmatrix}x_1\-x_2\end{bmatrix}=x_1\begin{bmatrix}1\0\end{bmatrix}+x_2\begin{bmatrix}0\-1\end{bmatrix}=\begin{bmatrix}1&0\0&-1\end{bmatrix}\begin{bmatrix}x_1\x_2\end{bmatrix}$$
令 $$\pmb{D}=\begin{bmatrix}1&0\0&-1\end{bmatrix}$$
称 $$\pmb{D}$$ 为标准反射矩阵。
更一般情况,求过原点的直线 $$L={t\pmb{v}_1|t\in\mathbb{R}}$$ 的反射矩阵,即以此直线为镜面。
令 $$\pmb{v}_2$$ 表示直线 $$L$$ 的法向量,即 $$\pmb{v}_2\bot\pmb{v}_1$$ ,如下图所示:
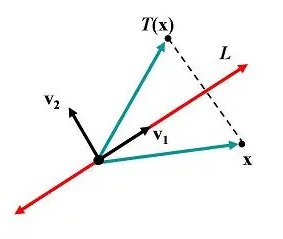
则:
$$\begin{split}\pmb{T}(\pmb{v}_1)&=\pmb{v}_1=1\cdot\pmb{v}_1\\pmb{T}(\pmb{v}_2)&=-\pmb{v}_2=(-1)\cdot\pmb{v}_2\end{split}\tag{3}$$
上面两个式子的形式相同,都是:
$$\pmb{T}(\pmb{v})=\lambda\pmb{v}\tag{4}$$
则称 $$\lambda$$ 为线性算子 $$\pmb{T}$$ 的特征值(eigenvalue),对应的非零向量 $$\pmb{v}$$ 为特征向量(eigenvector)。这两个量完全代表了线性算子 $$\pmb{T}$$ 的固有特征。
以(3)式为例,①特征向量 $$\pmb{v}_1,\pmb{v}_2$$ 经反射算子 $$\pmb{T}$$ 得到的像 $$\pmb{T}(\pmb{v}_i)$$ 属于子空间 $$span{\pmb{v}_1,\pmb{v}_2}$$ ,特征向量 $$\lambda_1,\lambda_2$$ 决定了 $$\pmb{T}(\pmb{v}_i)$$ 的伸缩倍数,正负号决定指向是否与原来相同;②除了特征空间 $$span{\pmb{v}_1,\pmb{v}_2}$$ ,其他不属于此子空间的非零向量皆不满足(4)式。
以上是以镜像发射变换为例。此外,线性算子 $$\pmb{T}$$ 还可以有其他意义。所以,没有一个确定的答案。
在(2)式中,表示矩阵 $$\pmb{A}$$ 用后面的方法得到,但是,(3)式中的镜像直线是一般的直线,不是x轴,无法用求表示矩阵 $$\pmb{D}$$ 方式计算出相应的表示矩阵。
下面探讨构建变换矩阵的方法。
将线性无关的特征向量组成 $$\mathbb{R}^2$$ 的一个基底 $$\pmb{\beta}={\pmb{v}_1,\pmb{v}_2}$$ ,任一向量 $$\pmb{x}\in\mathbb{R}^2$$ 可唯一表示成:
$$\pmb{x}=c_1\pmb{v}_1+c_2\pmb{v}_2$$
其中 $$c_1,c_2$$ 可以合并写成向量 $$\pmb{x}$$ 参考基底 $$\pmb{\beta}$$ 的向量,记作:$$[\pmb{x}]_{\pmb{\beta}}=\begin{bmatrix}c_1\c_2\end{bmatrix}$$
根据(3)式,可得:
$$\pmb{T}(\pmb{x})=\pmb{T}(c_1\pmb{v}_1+c_2\pmb{v}_2)=c_1\pmb{T}(\pmb{v}_1)+c_2\pmb{T}(\pmb{v}_2)=c_1\pmb{v}_1-c_2\pmb{v}_2\tag{5}$$
根据(5)式,可以写出 $$\pmb{T}(\pmb{x})$$ 参考基底 $$\pmb{\beta}$$ 的坐标向量:
$$[\pmb{T}(\pmb{x})]{\pmb{\beta}}=\begin{bmatrix}c_1\-c_2\end{bmatrix}=\begin{bmatrix}1&0\0&-1\end{bmatrix}\begin{bmatrix}c_1\c_2\end{bmatrix}=\pmb{D}[\pmb{x}]{\pmb{\beta}}\tag{6}$$
由此可知:若参考特征向量构成的基底,所有镜像反射矩阵必可转换成标准反射矩阵 $$\pmb{D}$$ 。
又因为:
$$\pmb{x}=c_1\pmb{v}_1+c_2\pmb{v}_2=\begin{bmatrix}\pmb{v}_1&\pmb{v}2\end{bmatrix}\begin{bmatrix}c_1\c_2\end{bmatrix}=\pmb{S}[\pmb{x}]{\pmb{\beta}}\tag{7}$$
若假设 $$\pmb{v}_1=\begin{bmatrix}2\1\end{bmatrix}\pmb{v}_2=\begin{bmatrix}-1\2\end{bmatrix}$$ ,则 $$\pmb{S}=\begin{bmatrix}\pmb{v}_1&\pmb{v}_2\end{bmatrix}=\begin{bmatrix}2&-1\1&2\end{bmatrix}$$ 称为坐标变换矩阵。
因为 $$[\pmb{x}]{\pmb{\beta}}=\pmb{S}^{-1}\pmb{x}$$ (由(7)式得),且 $$[\pmb{T}(\pmb{x})]{\pmb{\beta}}=\pmb{S}^{-1}\pmb{T}(\pmb{x})$$ ,代入(6)式:
$$\pmb{S}^{-1}\pmb{T}(\pmb{x})=\pmb{D}\pmb{S}^{-1}\pmb{x}$$
两边同时左乘 $$\pmb{S}$$ ,得:
$$\pmb{T}(\pmb{x})=\pmb{SD}\pmb{S}^{-1}\pmb{x}=\pmb{Ax}\tag{8}$$
将上述过程,可以用如下示意图表示:

所以,$$\pmb{T}$$ 的变换矩阵为:
$$\pmb{A}=\pmb{SD}\pmb{S}^{-1}=\begin{bmatrix}2&-1\1&2\end{bmatrix}\begin{bmatrix}1&0\0&-1\end{bmatrix}\frac{1}{5}\begin{bmatrix}2&1\-1&2\end{bmatrix}=\frac{1}{5}\begin{bmatrix}3&4\4&-3\end{bmatrix}$$
2021年5月20日深圳赛格大厦发生晃动,其元凶就是卡门涡流 $$^{[3]}$$ 引起的共振,这与1940年坍塌的美国华盛顿州的塔科马海峡吊桥 $$^{[4]}$$ 的原因相同。
下面就从特征值和特征向量的角度,理解自由振动系统的共振。
如图所示,物体质量 m ,令 $$x(t)$$ 表示弹簧于 $$t$$ 时刻的长度,根据胡克定律,弹簧的弹力为:
$$f(x)=-kx$$

由牛顿第二定律可得:
$$m\ddot{x}=-kx$$
因为指数函数具有微分不变性,所以,上述微分方程的解为:
$$x(t)=ue^{at}$$
由此可得:$$\ddot{x}=a^2ue^{at}=a^2x$$ ,所以:$$ma^2x=-kx$$ ,$$a^2=-\frac{k}{m}$$ ,故:
$$a=\pm i\sqrt{\frac{k}{m}}$$
令 $$\omega=\frac{k}{m}$$ ,$$x(t)$$ 可表示为特解 $$e^{i\omega t}$$ 和 $$e^{-i\omega t}$$ 的线性组合:
$$x(t)=\alpha_1e^{i\omega t}+\alpha_2e^{-i\omega t}$$
因为 $$x(t)$$ 是实函数,所以 $$\overline{x(t)}=x(t)$$ ,那么 $$\alpha_1$$ 和 $$\alpha_2$$ 是共轭复数,即 $$\alpha_2=\overline{\alpha_1}$$ 。
令 $$\alpha_1=\frac{1}{2}(c_1-ic_2)$$ ,$$c_1, c_2$$ 是实数,利用欧拉公式 $$e^{\pm i\theta}=\cos\theta\pm i\sin\theta$$ 可得:
$$\begin{split}x(t)&=\frac{1}{2}(c_1-ic_2)e^{i\omega t}+\frac{1}{2}(c_1+ic_2)e^{-i\omega t}\&=\frac{1}{2}(c_1-ic_2)(\cos(\omega t)+i\sin(\omega t))+\frac{1}{2}(c_1+ic_2)(\cos(\omega t)-i\sin(\omega t))\&=c_1\cos(\omega t)+c_2\sin(\omega t)\&=\hat{c}\cos(\omega t-\phi)\end{split}$$
其中 $$\hat{c} = \sqrt{c_1^2+c_2^2}$$ 表示振幅,$$\phi=\tan^{-1}(\frac{c_2}{c_1})$$ 是相位差,系数 $$c_1$$ 和 $$c_2$$ 由初始位置 $$x(0)$$ 和速度 $$\dot{x}(0)$$ 决定:
$$c_1 = x(0),\quad c_2=\frac{\dot{x}(0)}{\omega}$$
简谐振子以物体的平衡位置为中心,在 $$x=a$$ 和 $$x=-a$$ 之间以 $$T=\frac{2\pi}{\omega}$$ 为周期振动。
$$\omega = \frac{2\pi}{T}=\sqrt{\frac{k}{m}}$$
当物体质量越小,或劲度系数 k 越大,则振动频率越高。
如图所示,令 $$x_1=0$$ 和 $$x_2=0$$ 表示两个物体的平衡位置。

设从左向右,三个瘫痪的伸长量分别为 $$x_1, x_2-x_1, -x_2$$ ,有方程:
$$\begin{split}m\ddot{x}_1&=-k_1x_1+k_2(x_2-x_1)=-(k_1+k_2)x_1+k_2x_2\m\ddot{x}_2&=-k_2(x_2-x_1)+k_1(-x_2)=k_2x_1-(k_1+k_2)x_2\end{split}$$
写成矩阵形式:
$$\begin{bmatrix}\ddot{x}_1\\ddot{x}_2\end{bmatrix}+\begin{bmatrix}\frac{k_1+k_2}{m}&-\frac{k_2}{m}\-\frac{k_2}{m}&\frac{k_1+k_2}{m}\end{bmatrix}\begin{bmatrix}x_1\x_2\end{bmatrix}=\begin{bmatrix}0\0\end{bmatrix}$$
$$\ddot{\pmb{x}}+\pmb{Ax}=\pmb{0}$$
其中,$$\pmb{x}=\begin{bmatrix}x_1\x_2\end{bmatrix}$$ ,$$\pmb{A}=\begin{bmatrix}a&-b\-b&a\end{bmatrix}$$ 是实对称矩阵,$$a=\frac{k_1+k_2}{m}, b=\frac{k_2}{m}$$ 。
上述方程的解为:$$\pmb{x}(t)=\pmb{u}e^{i\omega t}$$ 。又:
$$\ddot{\pmb{x}}=-\pmb{u}\omega^2e^{i\omega t}=-\omega^2\pmb{x}$$
所以:
$$\pmb{Ax}=\omega^2\pmb{x}$$
$$\omega^2$$ 是 $$\pmb{A}$$ 的特征值,$$\omega$$ 又称为固有频率(特征值也称为固有值)。特征多项式:
$$\det(\pmb{A}-\lambda\pmb{I})=\begin{vmatrix}a-\lambda&-b\-b&a-\lambda\end{vmatrix}=(a-\lambda)^2-b^2$$
令上式为零,则得特征值:
$$\lambda_1=a+b=\frac{k_1+2k_2}{m}, \quad \lambda_2=a-b=\frac{k_1}{m}$$
其固有频率为 $$\omega_1=\sqrt{\lambda_1}=\sqrt{\frac{k_1+2k_2}{m}}$$ 和 $$\omega_2=\sqrt{\lambda_2}=\sqrt{\frac{k_1}{m}}$$ ,对应的特征向量:
$$\pmb{u}_1=\begin{bmatrix}1\-1\end{bmatrix}, \quad \pmb{u}_2=\begin{bmatrix}1\1\end{bmatrix}$$
则运动的位置 $$\pmb{x}(t)$$ 为:
$$\pmb{x}(t)=\alpha_1\pmb{u}_1e^{i\omega_1 t}+\alpha_2\pmb{u}_1e^{-i\omega_1 t}+\beta_1\pmb{u}_2e^{i\omega_2 t}+\beta_2\pmb{u}_2e^{-i\omega_2 t}$$
又因为 $$\pmb{x}(t)$$ 是实向量函数,$$\alpha_2=\overline{\alpha_1},\beta_2=\overline{\beta_1}$$ ,可得:
$$\pmb{x}(t)=c_{11}\pmb{u}1\cos(\omega_1 t)+c{12}\pmb{u}1\sin(\omega_1 t)+c{21}\pmb{u}2\cos(\omega_2 t)+c{22}\pmb{u}_2\sin(\omega_2 t)$$
其中,$$c_{11},c_{12},c_{21},c_{22}$$ 都是实数。当 $$t=0$$ 时,
$$\begin{split}\pmb{x}(0)&=c_{11}\pmb{u}1+c{21}\pmb{u}2\\dot{x}(0)&=\omega_1c{12}\pmb{u}1+\omega_2c{22}\pmb{u}_2\end{split}$$
所以得到:
$$\begin{split}c_{11}&=\frac{1}{2}(x_1(0)-x_2(0))\c_{21}&=\frac{1}{2}(x_1(0)+x_2(0))\c_{12}&=\frac{1}{2\omega_1}(\dot{x}_1(0)-\dot{x}2(0))\c{22}&=\frac{1}{2\omega_2}(\dot{x}_1(0)+\dot{x}_2(0))\end{split}$$
若两个物体在 $$t=0$$ 时静止,$$\dot{\pmb{x}}(0)=\pmb{0}$$ ,则 $$c_{12}=c_{22}=0$$ ,即得:
$$\pmb{x}(t)=c_{11}\pmb{u}1\cos(\omega_1 t)+c{21}\pmb{u}_2\cos(\omega_2 t)$$
两个物体的实际振动行为由初始位置决定,特征向量 $$\pmb{u}_1=\begin{bmatrix}1\-1\end{bmatrix}, \quad \pmb{u}_2=\begin{bmatrix}1\1\end{bmatrix}$$ 代表两种振型:
- 若 $$\pmb{x}(0)=r\pmb{u}1$$ ,则 $$c{11}=r$$ 且 $$c_{21}=0$$ ,故 $$\pmb{x}(t)=r\begin{bmatrix}1\-1\end{bmatrix}\cos(\omega_1 t)$$ ,这时两物体的振动频率为 $$\omega_1$$ ,相位差为 $$\pi$$ 。
- 若 $$\pmb{x}(0)=r\pmb{u}2$$ ,则 $$c{11}=0$$ 且 $$c_{21}=r$$ ,故 $$\pmb{x}(t)=r\begin{bmatrix}1\1\end{bmatrix}\cos(\omega_2 t)$$ ,这时两物体的振动频率为 $$\omega_2$$ ,相位差为 $$0$$ 。
[1]. 线代启示录:答Rich——关于特征值与特征向量的物理意义
[2]. 线代启示录:自由振动系统的特征值与特征向量
[3]. 维基百科:卡门涡流
[4]. 维基百科:塔科马海峡吊桥



