# Algoritmi e Strutture Dati in Javascript
[](https://github.com/trekhleb/javascript-algorithms/actions?query=workflow%3ACI+branch%3Amaster)
[](https://codecov.io/gh/trekhleb/javascript-algorithms)
Questa repository contiene esempi in Javascript dei più popolari algoritmi e strutture dati .
Ogni algortimo e struttura dati ha il suo README separato e la relative spiegazioni e i link per ulteriori approfondimenti (compresi quelli su YouTube).
_Leggilo in altre lingue:_
[_简体中文_](README.zh-CN.md),
[_繁體中文_](README.zh-TW.md),
[_한국어_](README.ko-KR.md),
[_日本語_](README.ja-JP.md),
[_Polski_](README.pl-PL.md),
[_Français_](README.fr-FR.md),
[_Español_](README.es-ES.md),
[_Português_](README.pt-BR.md),
[_Русский_](README.ru-RU.md),
[_Türk_](README.tr-TR.md),
[_Bahasa Indonesia_](README.id-ID.md),
[_Українська_](README.uk-UA.md),
[_Arabic_](README.ar-AR.md),
[_Tiếng Việt_](README.vi-VN.md),
[_Deutsch_](README.de-DE.md)
*☝ Si noti che questo progetto è destinato ad essere utilizzato solo per l'apprendimento e la ricerca e non è destinato ad essere utilizzato per il commercio.*
## Strutture Dati
Una struttura dati è un particolare modo di organizzare e memorizzare i dati in un computer che permeta di accedervi e modificarli in modo efficiente. Più precisamente, una struttura dati è una raccolta di dati, le relazioni tra di essi e le funzioni o operazioni che possono essere applicate ai dati.
`P` - Principiante, `A` - Avanzato
* `P` [Lista Concatenata](src/data-structures/linked-list)
* `P` [Doppia Lista Concatenata](src/data-structures/doubly-linked-list)
* `P` [Coda](src/data-structures/queue)
* `P` [Pila](src/data-structures/stack)
* `P` [Hash Table](src/data-structures/hash-table)
* `P` [Heap](src/data-structures/heap) - versione massimo e minimo heap
* `P` [Coda di priorità](src/data-structures/priority-queue)
* `A` [Trie](src/data-structures/trie)
* `A` [Albero](src/data-structures/tree)
* `A` [Albero binario di ricerca](src/data-structures/tree/binary-search-tree)
* `A` [Albero AVL](src/data-structures/tree/avl-tree)
* `A` [RB Albero](src/data-structures/tree/red-black-tree)
* `A` [Albero Segmentato](src/data-structures/tree/segment-tree) - con min/max/sum esempi di query
* `A` [Albero di Fenwick](src/data-structures/tree/fenwick-tree) (Albero binario indicizzato)
* `A` [Grafo](src/data-structures/graph) (direzionale e unidirezionale)
* `A` [Set Disgiunto](src/data-structures/disjoint-set)
* `A` [Filtro Bloom](src/data-structures/bloom-filter)
## Algoritmi
Un algoritmo è una specifica univoca per risolvere una classe di problemi. È
un insieme di regole che definiscono con precisione una sequenza di operazioni.
`P` - Principiante, `A` - Avanzato
### Algoritmi per Topic
* **Matematica**
* `P` [Manipolazione dei Bit](src/algorithms/math/bits) - set/get/update/clear bits, moltiplicazione/divisione per due, gestire numeri negativi etc.
* `P` [Fattoriale](src/algorithms/math/factorial)
* `P` [Numeri di Fibonacci](src/algorithms/math/fibonacci) - classico e forma chiusa
* `P` [Test di Primalità](src/algorithms/math/primality-test) (metodo del divisore)
* `P` [Algoritmo di Euclide](src/algorithms/math/euclidean-algorithm) - trova il massimo comune divisore (MCD)
* `P` [Minimo Comune Multiplo](src/algorithms/math/least-common-multiple) (MCM)
* `P` [Crivello di Eratostene](src/algorithms/math/sieve-of-eratosthenes) - trova i numeri i primi fino al limite indicato
* `P` [Potenza di due](src/algorithms/math/is-power-of-two) - controlla se il numero è una potenza di due
* `P` [Triangolo di Pascal](src/algorithms/math/pascal-triangle)
* `P` [Numeri Complessi](src/algorithms/math/complex-number) - numeri complessi e operazioni
* `P` [Radiante & Gradi](src/algorithms/math/radian) - conversione da radiante a gradi e viceversa
* `P` [Potenza di un Numero](src/algorithms/math/fast-powering)
* `A` [Partizione di un Intero](src/algorithms/math/integer-partition)
* `A` [Radice Quadrata](src/algorithms/math/square-root) - Metodo di Newton
* `A` [Algoritmo di Liu Hui π](src/algorithms/math/liu-hui) - calcolare π usando un poligono
* `A` [Trasformata Discreta di Fourier ](src/algorithms/math/fourier-transform) -decomporre una funzione di tempo (un segnale) nelle frequenze che lo compongono
* **Set**
* `P` [Prodotto Cartesiano](src/algorithms/sets/cartesian-product) - moltiplicazione multipla di set
* `P` [Fisher–Yates Shuffle](src/algorithms/sets/fisher-yates) - permutazione casuale di un sequenza finita
* `A` [Power Set](src/algorithms/sets/power-set) - tutti i sottoinsiemi di un set (soluzioni bitwise e backtracking)
* `A` [Permutazioni](src/algorithms/sets/permutations) (con e senza ripetizioni)
* `A` [Combinazioni](src/algorithms/sets/combinations) (con e senza ripetizioni)
* `A` [Massima Sottosequenza Comune](src/algorithms/sets/longest-common-subsequence) (LCS)
* `A` [Massima Sottosequenza Crescente](src/algorithms/sets/longest-increasing-subsequence)
* `A` [Minima Sottosequenza Diffusa](src/algorithms/sets/shortest-common-supersequence) (SCS)
* `A` [Problema dello Zaino di Knapsack](src/algorithms/sets/knapsack-problem) - "0/1" e "Senza Restrizioni"
* `A` [Massimo SubArray](src/algorithms/sets/maximum-subarray) - "Brute Force" e "Programmazione Dinamica" versione Kadane
* `A` [Somma di Combinazioni](src/algorithms/sets/combination-sum) - ricerca di tutte le combinazioni di una somma
* **String**
* `P` [Distanza di Hamming](src/algorithms/string/hamming-distance) - numero di posizioni in cui i caratteri sono diversi
* `A` [Distanza di Levenshtein](src/algorithms/string/levenshtein-distance) - numero minimo di modifiche per rendere uguali due stringhe
* `A` [Algoritmo di Knuth-Morris-Pratt](src/algorithms/string/knuth-morris-pratt) (KMP) - ricerca nella sottostringa (pattern matching)
* `A` [Algoritmo Z](src/algorithms/string/z-algorithm) - ricerca nella sottostringa (pattern matching)
* `A` [Algoritmo di Rabin Karp ](src/algorithms/string/rabin-karp) - ricerca nella sottostringa
* `A` [Sottostringa Comune più lunga](src/algorithms/string/longest-common-substring)
* `A` [Espressioni Regolari](src/algorithms/string/regular-expression-matching)
* **Searches**
* `P` [Ricerca Sequenziale](src/algorithms/search/linear-search)
* `P` [Ricerca a Salti](src/algorithms/search/jump-search) (o Ricerca a Blocchi) - per la ricerca in array ordinati
* `P` [Ricerca Binari](src/algorithms/search/binary-search) - per la ricerca in array ordinati
* `P` [Ricerca Interpolata](src/algorithms/search/interpolation-search) - per la ricerca in un array ordinato uniformemente distibuito
* **Sorting**
* `P` [Bubble Sort](src/algorithms/sorting/bubble-sort)
* `P` [Selection Sort](src/algorithms/sorting/selection-sort)
* `P` [Insertion Sort](src/algorithms/sorting/insertion-sort)
* `P` [Heap Sort](src/algorithms/sorting/heap-sort)
* `P` [Merge Sort](src/algorithms/sorting/merge-sort)
* `P` [Quicksort](src/algorithms/sorting/quick-sort) - con e senza allocazione di ulteriore memoria
* `P` [Shellsort](src/algorithms/sorting/shell-sort)
* `P` [Counting Sort](src/algorithms/sorting/counting-sort)
* `P` [Radix Sort](src/algorithms/sorting/radix-sort)
* **Lista Concatenatas**
* `P` [Attraversamento Lista Concatenata](src/algorithms/linked-list/traversal)
* `P` [Attraversamento Lista Concatenata nel senso Contrario](src/algorithms/linked-list/reverse-traversal)
* **Alberi**
* `P` [Ricerca in Profondità su Alberi](src/algorithms/tree/depth-first-search) (DFS)
* `P` [Ricerca in Ampiezza su Alberi](src/algorithms/tree/breadth-first-search) (BFS)
* **Grafi**
* `P` [Ricerca in Profondità su Grafi](src/algorithms/graph/depth-first-search) (DFS)
* `P` [Breadth-First Search su Grafi](src/algorithms/graph/breadth-first-search) (BFS)
* `P` [Algoritmo di Kruskal](src/algorithms/graph/kruskal) - ricerca dell'Albero con Minima Distanza (MST) per grafi pesati unidirezionali
* `A` [Algoritmo di Dijkstra](src/algorithms/graph/dijkstra) - ricerca dei percorsi più breve per raggiungere tutti i vertici del grafo da un singolo vertice
* `A` [Algoritmo di Bellman-Ford](src/algorithms/graph/bellman-ford) - ricerca dei percorsi più breve per raggiungere tutti i vertici del grafo da un singolo vertice
* `A` [Algoritmo di Floyd-Warshall](src/algorithms/graph/floyd-warshall) - ricerca dei percorsi più brevi tra tutte le coppie di vertici
* `A` [Rivelamento dei Cicli](src/algorithms/graph/detect-cycle) - per grafici diretti e non diretti (basate su partizioni DFS e Disjoint Set)
* `A` [Algoritmo di Prim](src/algorithms/graph/prim) - ricerca dell'Albero Ricoprente Minimo (MST) per grafi unidirezionali pesati
* `A` [Ordinamento Topologico](src/algorithms/graph/topological-sorting) - metodo DFS
* `A` [Punti di Articolazione](src/algorithms/graph/articulation-points) - Algoritmo di Tarjan (basato su DFS)
* `A` [Bridges](src/algorithms/graph/bridges) - basato su DFS
* `A` [Cammino Euleriano e Circuito Euleriano](src/algorithms/graph/eulerian-path) - Algoritmo di Fleury - Visita ogni margine esattamente una volta
* `A` [Ciclo di Hamiltonian](src/algorithms/graph/hamiltonian-cycle) - Visita ad ogni vertice solo una volta
* `A` [Componenti Fortemente Connessa](src/algorithms/graph/strongly-connected-components) - algoritmo di Kosaraju
* `A` [Problema del Commesso Viaggiatore](src/algorithms/graph/travelling-salesman) - il percorso più breve che visita ogni città e ritorna alla città iniziale
* **Crittografia**
* `P` [Hash Polinomiale](src/algorithms/cryptography/polynomial-hash) - Una funzione hash di rolling basata sul polinomio
* **Senza categoria**
* `P` [Torre di Hanoi](src/algorithms/uncategorized/hanoi-tower)
* `P` [Rotazione Matrice Quadrata](src/algorithms/uncategorized/square-matrix-rotation) - algoritmo in memoria
* `P` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, programmazione dinamica (top-down + bottom-up) ed esempre di greeedy
* `P` [Percorsi Unici](src/algorithms/uncategorized/unique-paths) - backtracking, programmazione dinamica and l'esempio del Triangolo di Pascal
* `P` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - problema dell'acqua piovana in trappola(versione con programmazione dinamica e brute force)
* `P` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - contare il numero di percorsi per arrivare in vetta(4 soluzioni)
* `A` [Rompicapo delle Otto Regine](src/algorithms/uncategorized/n-queens)
* `A` [Percorso del Cavallo](src/algorithms/uncategorized/knight-tour)
### Modelli di Algoritmi
Un modello di algoritmo è un generico metodo o approcio che sta alla base della progettazione di una classe di algoritmi.
Si tratta di un'astrazione ancora più alta di un algoritmo, proprio come un algoritmo è un'astrazione di un programma del computer.
* **Brute Force** - controlla tutte le possibilità e seleziona la migliore
* `P` [Ricerca Lineare](src/algorithms/search/linear-search)
* `P` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - problema dell'acqua piovana in trappola
* `P` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - contare il numero di percorsi per arrivare in vetta
* `A` [Massimo SubArray](src/algorithms/sets/maximum-subarray)
* `A` [Problema del commesso viaggiatore](src/algorithms/graph/travelling-salesman) - il percorso più breve che visita ogni città e ritorna alla città iniziale
* `A` [Trasformata Discreta di Fourier](src/algorithms/math/fourier-transform) - scomporre la funzione (segnale) del tempo in frequenze che la compongono
* **Greedy** - scegliere l'opzione migliore al momento d'eleborazione dell'algoritmo, senza alcuna considerazione per il futuro
* `P` [Jump Game](src/algorithms/uncategorized/jump-game)
* `A` [Problema dello Zaino di Knapsack](src/algorithms/sets/knapsack-problem)
* `A` [Algoritmo di Dijkstra](src/algorithms/graph/dijkstra) - ricerca del percorso più breve tra tutti i vertici del grafo
* `A` [Algoritmo di Prim](src/algorithms/graph/prim) - ricerca del Minimo Albero Ricoprente per grafi pesati e unidirezionali
* `A` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - finding Minimum Spanning Tree (MST) for weighted undirected graph
* **Divide e Conquista** - divide il problema in piccole parti e risolve ogni parte
* `P` [Ricerca Binaria](src/algorithms/search/binary-search)
* `P` [Torre di Hanoi](src/algorithms/uncategorized/hanoi-tower)
* `P` [Triangolo di Pascal](src/algorithms/math/pascal-triangle)
* `P` [Algoritmo di Euclide](src/algorithms/math/euclidean-algorithm) - calculate the Greatest Common Divisor (GCD)
* `P` [Merge Sort](src/algorithms/sorting/merge-sort)
* `P` [Quicksort](src/algorithms/sorting/quick-sort)
* `P` [Albero per Ricerca in Profondità](src/algorithms/tree/depth-first-search) (DFS)
* `P` [Grafo per Ricerca in Profondità](src/algorithms/graph/depth-first-search) (DFS)
* `P` [Jump Game](src/algorithms/uncategorized/jump-game)
* `P` [Algoritmo di Elevamento a Potenza](src/algorithms/math/fast-powering)
* `A` [Permutazioni](src/algorithms/sets/permutations) (con o senza ripetizioni)
* `A` [Combinazioni](src/algorithms/sets/combinations) (con o senza ripetizioni)
* **Programmazione Dinamica** - creare una soluzione utilizzando le sub-solution trovate in precedenza
* `P` [Numero di Fibonacci](src/algorithms/math/fibonacci)
* `P` [Jump Game](src/algorithms/uncategorized/jump-game)
* `P` [Percorsi Unici](src/algorithms/uncategorized/unique-paths)
* `P` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - problema dell'acqua piovana in trappola
* `P` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - contare il numero di percorsi per arrivare in vetta
* `A` [Distanza di Levenshtein](src/algorithms/string/levenshtein-distance) - minima variazione tra due sequenze
* `A` [La Più Lunga Frequente SottoSequenza](src/algorithms/sets/longest-common-subsequence) (LCS)
* `A` [La Più Lunga Frequente SubString](src/algorithms/string/longest-common-substring)
* `A` [La Più Lunga SottoSequenza Crescente](src/algorithms/sets/longest-increasing-subsequence)
* `A` [La Più Corta e Frequente SuperSequenza](src/algorithms/sets/shortest-common-supersequence)
* `A` [Problema dello zaino](src/algorithms/sets/knapsack-problem)
* `A` [Partizione di un Intero](src/algorithms/math/integer-partition)
* `A` [Massimo SubArray](src/algorithms/sets/maximum-subarray)
* `A` [Algoritmo di Bellman-Ford](src/algorithms/graph/bellman-ford) - ricerca del percorso più breve per tutti i vertici del grafo
* `A` [Algoritmo di Floyd-Warshall](src/algorithms/graph/floyd-warshall) - ricerca del percorso più breve tra tutte le coppie di vertici
* `A` [Espressioni Regolari](src/algorithms/string/regular-expression-matching)
* **Backtracking** - come la brute force, provate a generare tutte le soluzioni possibili, ma ogni volta che generate la prossima soluzione testate se soddisfa tutte le condizioni e solo allora continuare a generare soluzioni successive. Altrimenti, fate marcia indietro, e andate su un percorso diverso per trovare una soluzione. Normalmente si utilizza l'algoritmo DFS.
* `P` [Jump Game](src/algorithms/uncategorized/jump-game)
* `P` [Percorsi Unici](src/algorithms/uncategorized/unique-paths)
* `P` [Power Set](src/algorithms/sets/power-set) - tutti i subset di un set
* `A` [Ciclo di Hamiltonian](src/algorithms/graph/hamiltonian-cycle) - visita di tutti i vertici solamente una volta
* `A` [Problema di N-Queens](src/algorithms/uncategorized/n-queens)
* `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
* `A` [Combinazioni di una Somma](src/algorithms/sets/combination-sum) - trovare tutte le combinazioni che compongono una somma
* **Branch & Bound** - ricordatevi che la soluzione meno costosa trovata ad ogni step durante il backtracking e
il costo di usare la soluzione meno costosa trovata fino al limite inferiore al costo minimo della soluzione al problema,
al fine di scartare soluzioni parziali con costi maggiori della soluzione meno costosa trovata .
Di solito si usa BFS trasversale in combinazione con DFS trasversale .
## Come usare questa repository
**Installare tutte le dipendenze**
```
npm install
```
**Eseguire ESLint**
Potresti usarlo per controllare la qualità del codice.
```
npm run lint
```
**Eseguire tutti i test**
```
npm test
```
**Eseguire un test tramite il nome**
```
npm test -- 'LinkedList'
```
**Playground**
Se vuoi puoi giocare le strutture dati e gli algoritmi nel file ./src/playground/playground.js` e
scrivere test nel file `./src/playground/__test__/playground.test.js`.
Poi puoi semplicemente eseguire il seguente comando per testare quello che hai scritto :
```
npm test -- 'playground'
```
## Informazioni Utili
### Bibliografia
[▶ Data Structures and Algorithms on YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
### Notazione Big O
* La notazione Big O* è usata per classificare algoritmi in base al tempo di esecuzione o ai
requisiti di spazio che crescono in base alla crescita dell'input .
Nella grafico qua sotto puoi trovare gli ordini di crescita più comuni degli algoritmi usando la notazione Big O.
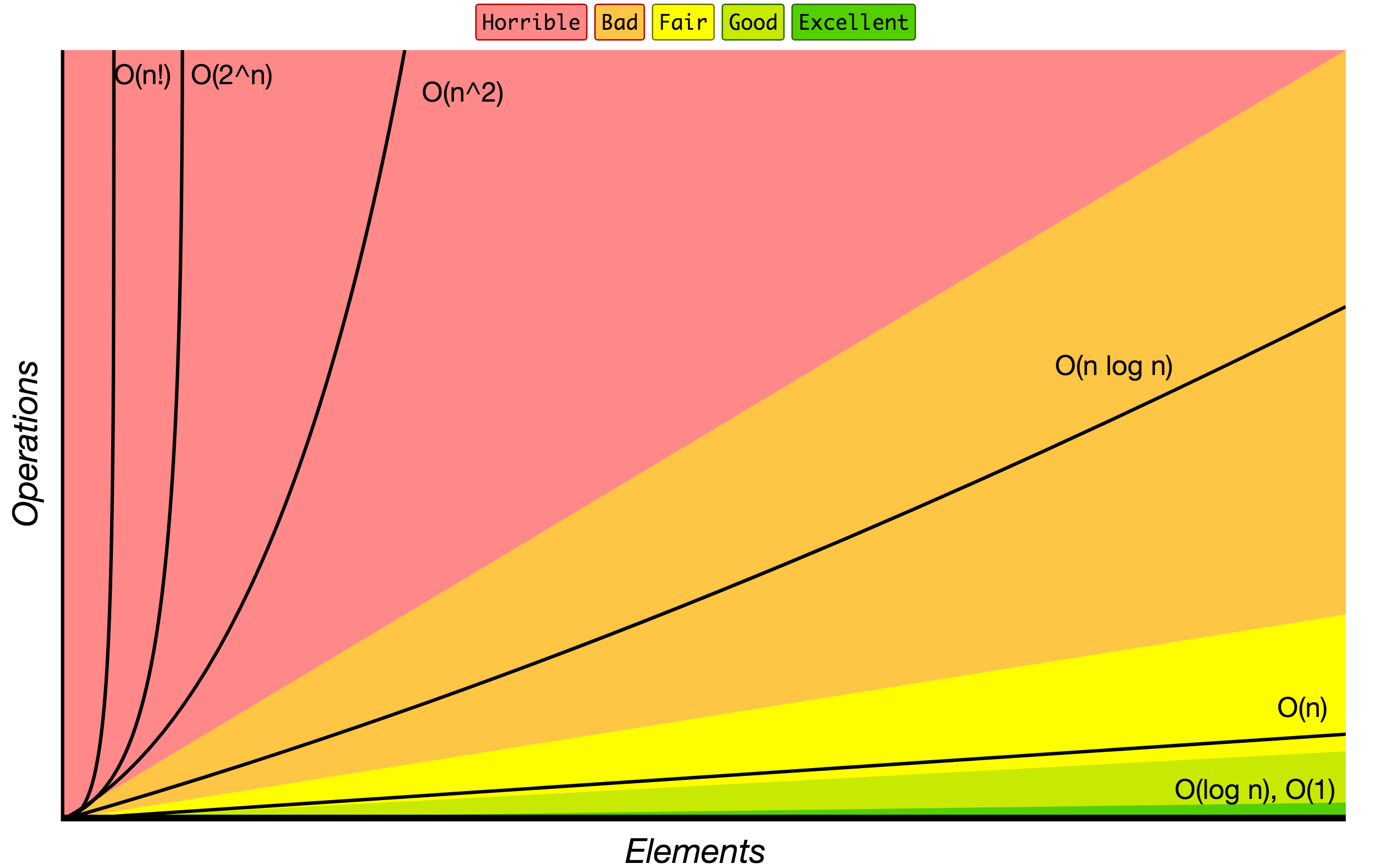
Riferimento: [Big O Cheat Sheet](http://bigocheatsheet.com/).
Nella tabella qua sotto ci sono riportate la lista delle notazioni Big O più usate e delle loro prestazioni comparate tra differenti grandezze d'input .
| Notazione Big O | Computazione con 10 elementi | Computazione con 100 elementi | Computazione con 1000 elementi |
| --------------- | ---------------------------- | ----------------------------- | ------------------------------- |
| **O(1)** | 1 | 1 | 1 |
| **O(log N)** | 3 | 6 | 9 |
| **O(N)** | 10 | 100 | 1000 |
| **O(N log N)** | 30 | 600 | 9000 |
| **O(N^2)** | 100 | 10000 | 1000000 |
| **O(2^N)** | 1024 | 1.26e+29 | 1.07e+301 |
| **O(N!)** | 3628800 | 9.3e+157 | 4.02e+2567 |
### Complessità delle Operazion sulle Strutture Dati
| Struttura Dati | Accesso | Ricerca | Inserimento | Rimozione | Commenti |
| ----------------------- | :-------: | :-------: | :--------: | :-------: | :-------- |
| **Array** | 1 | n | n | n | |
| **Pila** | n | n | 1 | 1 | |
| **Coda** | n | n | 1 | 1 | |
| **Lista Concatenata** | n | n | 1 | n | |
| **Tabella Hash** | - | n | n | n | Nel caso di una funzione di hashing perfetta il costo sarebbe O(1)|
| **Binary Search Tree** | n | n | n | n | Nel caso di albero bilanciato il costo sarebbe O(log(n)) |
| **B-Tree** | log(n) | log(n) | log(n) | log(n) | |
| **Red-Black Tree** | log(n) | log(n) | log(n) | log(n) | |
| **Albero AVL** | log(n) | log(n) | log(n) | log(n) | |
| **Bloom Filter** | - | 1 | 1 | - | Falsi positivi sono possibili durante la ricerca |
### Complessità degli Algoritmi di Ordinamento di Array
| Nome | Milgiore | Media | Perggiore | Memoria | Stabile | Commenti |
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
| **Bubble sort** | n | n2 | n2 | 1 | Yes | |
| **Insertion sort** | n | n2 | n2 | 1 | Yes | |
| **Selection sort** | n2 | n2 | n2 | 1 | No | |
| **Heap sort** | n log(n) | n log(n) | n log(n) | 1 | No | |
| **Merge sort** | n log(n) | n log(n) | n log(n) | n | Yes | |
| **Quick sort** | n log(n) | n log(n) | n2 | log(n) | No | Quicksort viene eseguito in memoria solitamente con una pila di O(log(n)) |
| **Shell sort** | n log(n) | dipende dagli spazi vuoti nella sequenza | n (log(n))2 | 1 | No | |
| **Counting sort** | n + r | n + r | n + r | n + r | Yes | r - numero più grande nell'array |
| **Radix sort** | n * k | n * k | n * k | n + k | Yes | k - lunghezza della chiave più grande |
> ℹ️ A few more [projects](https://trekhleb.dev/projects/) and [articles](https://trekhleb.dev/blog/) about JavaScript and algorithms on [trekhleb.dev](https://trekhleb.dev)