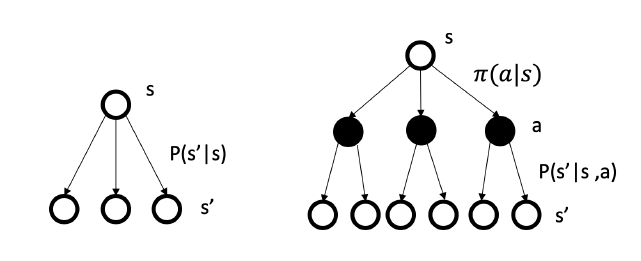
Both MRP and MDP obey Markovian property, i.e. "the future is independent of the past if present state is given".
Markov reward model or Markov reward process is a stochastic process which extends either a Markov chain or continuous-time Markov chain by adding a reward rate to each state. (from wiki).
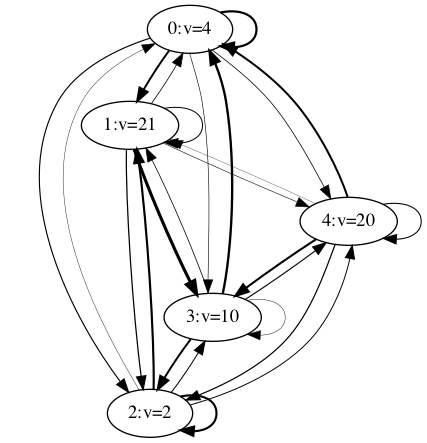
In MRP, each state returns a reward, and the transition of states are only related to the current state.
The transition probability is:
The reward of each state is defined as a one-param function:
python MRP_value_compute.py
=== [*] Testing Monte Carlo for Markov Reward Process
[*] gamma is :0.9, trajectory length is :50
===== evaluation for state 0
>>> Test 99 for state 0, gain is 99.02934189439594
>>> Test 199 for state 0, gain is 106.79418112727177
>>> Test 299 for state 0, gain is 115.50706990514294
>>> Test 399 for state 0, gain is 76.22562463033262
>>> Test 499 for state 0, gain is 107.49870133662205
>>> Avg gain for state 0 is 96.1450
===== evaluation for state 1
>>> Test 99 for state 1, gain is 112.79632533138894
>>> Test 199 for state 1, gain is 130.86851918706282
>>> Test 299 for state 1, gain is 107.46136245054069
>>> Test 399 for state 1, gain is 128.68299741911875
>>> Test 499 for state 1, gain is 116.71395891605708
>>> Avg gain for state 1 is 113.0258
===== evaluation for state 2
>>> Test 99 for state 2, gain is 116.14071153305498
>>> Test 199 for state 2, gain is 76.67419236735378
>>> Test 299 for state 2, gain is 92.6041745039313
>>> Test 399 for state 2, gain is 106.68196092797285
>>> Test 499 for state 2, gain is 95.22321585363706
>>> Avg gain for state 2 is 96.2923
===== evaluation for state 3
>>> Test 99 for state 3, gain is 75.31720076906447
>>> Test 199 for state 3, gain is 103.38728238522592
>>> Test 299 for state 3, gain is 83.56701540915144
>>> Test 399 for state 3, gain is 106.50320105629395
>>> Test 499 for state 3, gain is 97.64504188077204
>>> Avg gain for state 3 is 101.0259
===== evaluation for state 4
>>> Test 99 for state 4, gain is 87.21322203433647
>>> Test 199 for state 4, gain is 120.33660008273363
>>> Test 299 for state 4, gain is 114.8313250249045
>>> Test 399 for state 4, gain is 100.88108184673797
>>> Test 499 for state 4, gain is 108.00491629077322
>>> Avg gain for state 4 is 110.9691
[96.14504707518711, 113.02584121241367, 96.29229617334056, 101.02585099222453, 110.96914341806736]
[ 4 21 2 10 20]
=== [*] Testing Iterative Algorithm (DP) for Markov Reward Process
[*] gamma is : 0.9, epsilon is : 0.01
current values: [ 4. 21.4209059 8.47897487 15.75373839 27.72796956], residue: 77.38158871644981
current values: [16.26945824 35.69129327 21.54301149 29.77640383 41.70045093], residue: 67.59902904168807
current values: [28.27991231 47.96973373 33.26497621 40.95425472 52.52356965], residue: 58.01182886698946
......
current values: [ 97.5631903 113.45405817 96.50642363 101.50022143 111.35105024], residue: 0.012737502460552719
current values: [ 97.56554398 113.45627564 96.50856523 101.50227471 111.35304571], residue: 0.01076150100044515
current values: [ 97.56753252 113.45814912 96.51037459 101.50400946 111.35473162], residue: 0.009092041720151656
[ 97.56753252 113.45814912 96.51037459 101.50400946 111.35473162]
[ 4 21 2 10 20]
Left means MRP, right is MDP. Actions matter in MDP!
Markov decision process (MDP) is a discrete-time stochastic control process. It provides a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker. (from wiki)
The transition probability from state S_i to S_j under action A_k is defined as follows:
The reward function of MDP has two parameters: