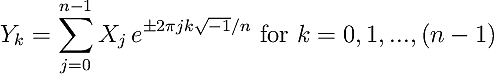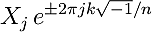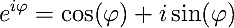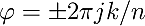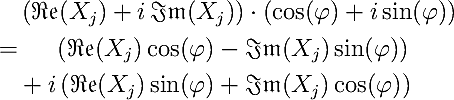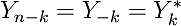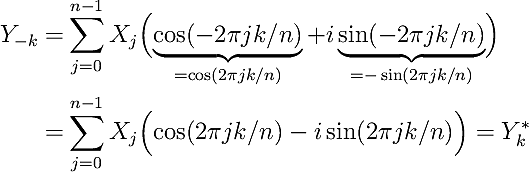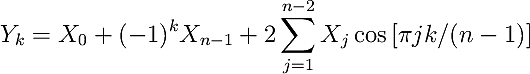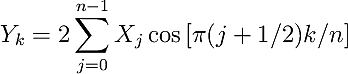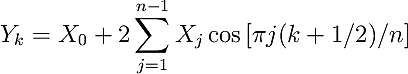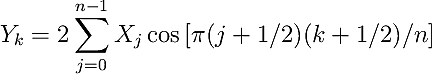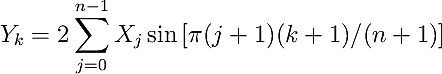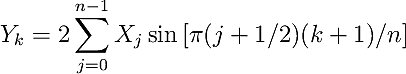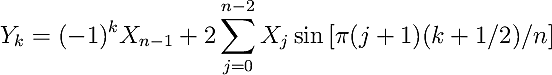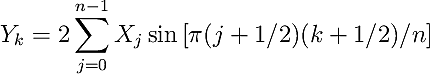This is a basic C project (Makefile, but also for the Eclipse IDE) I use for exploring FFTW 3.3.9.
One- and two-dimensional discrete Fourier transforms (DFTs) of random data are computed using both FFTW and straight-forward naive algorithms in order to illustrate explicitly what kind of symmetries and scaling properties FFTW implies in its inputs and outputs.
This tutorial starts by computing one-dimensional (1D) DFTs of random input data.
The first example is basically a self-contained version of the corresponding example in the FFTW manual.
We want to compute the complex-valued one-dimensional DFT here, which is specified in section 4.8.1 of the FFTW reference manual.
The sign in the exponent of the basis function specifies the direction in which the Fourier transform is to be computed:
-1 indicates a "forward" transform and +1 indicates a backward transform. These values are available via the FFTW_FORWARD and FFTW_BACKWARD preprocessor macros.
In order to compute the DFT, complex-valued products of the following form need to be evaluated:
Eulers formula comes in handy now (where i is the imaginary unit with i^2=-1):
The angle argument phi can be identified in above formulas for the DFT:
Now the complex-valued product can be computed using only real-valued variables:
FFTW implements all this math internally and the explicit formulation was only used to build a basis for the computations to follow.
Below is the example code showing how to compute the 1d c2c DFT using both FFTW and a manual implementation.
The size of the DFT is specified via the variable n and the direction (forward or backward) is specified via the variable dir.
Complex-valued arrays in, ref_out and fftw_out are allocated to hold the input (X_k) and outputs (Y_k) of the DFT.
A plan for the corresponding DFT is created using fftw_plan_dft_1d.
Only after this, the input data is written into the in array.
The reference output is computed now (before calling fftw_execute), since in some later examples (most notably multi-dimensional c2r transforms),
FFTW overwrites the input data and for good practise, we keep this in mind already now.
Note that this is an out-of-place transform, since in and fftw_out are allocated to be separate arrays.
Next the FFTW transform can be executed via fftw_execute.
This fills the corresponding output array fftw_out, which is subsequently compared against the reference output in ref_out.
A conservative tolerance of 1e-12 is specified to make the example work also for weird input data (as generated by the PRNG).
The actual deviations are usually much smaller and can be observed in the screen output from compare_1d_cplx.
Finally, the fftw_plan is destroyed and the memory is released using fftw_free (which has to be used if the array was allocated using fftw_alloc_*).
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <complex.h>
#include <fftw3.h>
#include "util.h"
void test_1d_c2c() {
int n = 32;
int dir = FFTW_BACKWARD;
double real, imag, phi;
fftw_complex *in = fftw_alloc_complex(n);
fftw_complex *ref_out = fftw_alloc_complex(n);
fftw_complex *fftw_out = fftw_alloc_complex(n);
fftw_plan p = fftw_plan_dft_1d(n, in, fftw_out, dir, FFTW_ESTIMATE);
// fill the input array with random data
fill_random_1d_cplx(n, in);
// compute the reference output
for (int k = 0; k < n; ++k) {
ref_out[k] = 0.0;
for (int j = 0; j < n; ++j) {
phi = dir * 2.0 * M_PI * j * k / ((double) n);
real = creal(in[j]) * cos(phi) - cimag(in[j]) * sin(phi);
imag = creal(in[j]) * sin(phi) + cimag(in[j]) * cos(phi);
ref_out[k] += real + I * imag;
}
}
// compute the DFT of in using FFTW
fftw_execute(p);
// compare reference output with FFTW output
double eps = 1e-12;
compare_1d_cplx(n, ref_out, fftw_out, eps);
fftw_destroy_plan(p);
fftw_free(in);
fftw_free(ref_out);
fftw_free(fftw_out);
}
int main(int argc, char** argv) {
test_1d_c2c();
return 0;
}The code is available in the file src/test_1d_c2c.c.
The next two examples deal with DFTs of purely real data (r2c) and DFTs which produce purely real data (c2r).
These are covered in the official FFTW tutorial
as well as in the FFTW reference manual.
In case either the input array or the output array are constrained to be purely real, the corresponding complex-valued output or input array
features Hermitian symmetry (where the n-periodicity has been included as well):
For the case of a DFT of real-valued X_j and complex-valued Y_k with Hermitian symmetry, the Fourier sum is written out excplicitly as follows:
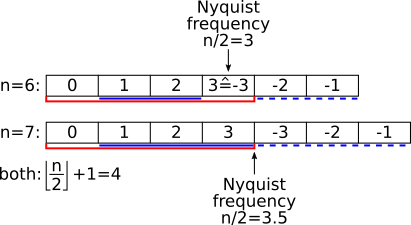
The figure below illustrates the structure of the complex-valued Fourier space arrays
occuring in the DFT for both even-valued (n=6) and odd-valued (n=7) sizes of the DFT.
The size required to contain all information required for the transform from or to a real-valued array
is contained in the first n/2+1 (division by 2 rounded down) entries of the complex array, indicated by the red bars in above figure.
For both even and odd values of n, Hermitian symmetry implies Y_0 = Y*_0 and thus Y_0 is always real.
In the case of even n, we can intuitively observe that Y_m = Y*_-m where m=n/2 (the element at the Nyquist frequency,
and thus also the last element of the complex-valued Fourier-space array) is also purely real.
The DFT formulation includes all elements of the Fourier-space array from 0 to n-1.
Now that only parts of these coefficients are taken into account, they have to be weighted appropriately
to recover the results that would have been obtained by using the full array without taking advantage of its symmetry properties.
For odd n, all components of the Fourier-space array except the DC element at k=0 have to be weighted with a factor of 2.
For even n, all components of the Fourier-space array except the DC element at k=0 and the Nyquist element at k=n/2
have to be weighted with a factor of 2.
The elements that need to be weighted by a factor of 2 are highlighted by solid blue lines in above illustration.
The redundant elements that are not explicitly needed are indicated by dashed blue lines.
The transformation from complex Fourier space to real-valued real space is demonstrated in src/test_1d_c2r.c.
The relevant portion of the source code is here:
int nCplx = n / 2 + 1;
for (int k = 0; k < n; ++k) {
// start with DC component, which is purely real due to Hermitian symmetry
ref_out[k] = creal(in[0]);
int loopEnd = nCplx;
// special case for even n
if (n % 2 == 0) {
// Nyquist element is purely real as well
phi = 2.0 * M_PI * (nCplx - 1) * k / ((double) n);
ref_out[k] += creal(in[nCplx - 1]) * cos(phi);
loopEnd = nCplx-1;
}
// middle elements are handled the same for even and odd n
for (int j = 1; j < loopEnd; ++j) {
phi = 2.0 * M_PI * j * k / ((double) n);
real = creal(in[j]) * cos(phi) - cimag(in[j]) * sin(phi);
ref_out[k] += 2.0 * real;
}
}Note that the integer division used to compute nCplx (correctly) rounds down.
The rest is a relatively straight-forward implementation of above verbose algorithm.
The DC component is always taken to be real.
Depending on whether n is even or odd, the number of elements to take into account with both real and imaginary component (loopEnd) is adjusted.
The (purely real) Nyquist element at n/2 is added separately if n is even.
All other elements are weighted by a factor of 2 and only the real part
of the complex product of input Fourier coefficient and complex-valued basis function is actually computed.
The reverse transform from real space to Fourier space is comparably simple to implement:
for (int k = 0; k < nCplx; ++k) {
// DC component is always real
ref_out[k] = in[0];
for (int j = 1; j < n; ++j) {
phi = -2.0 * M_PI * j * k / ((double) n);
real = in[j] * cos(phi);
imag = in[j] * sin(phi);
ref_out[k] += real + I * imag;
}
}Note that in this case, only the non-redundant part of the complex-values Fourier coefficients need to be computed
from a real-valued input. The separate handling of the DC component is not strictly necessary, since cos(0)=1 and sin(0)=0
and thus the DC component would get no imaginary contribution.
The full example is available in the file src/test_1d_r2c.c.
It becomes evident in above examples that the sign of a c2r DFT is always FFTW_BACKWARD and
the sign of a r2c DFT is always FFTW_FORWARD.
Certain symmetries can be assumed for a given real input array of which a DFT is to be computed
that lead to the output array being purely real as well. This is another gain of a factor of 2 in speed
and memory usage over r2c/c2r transforms.
Depending on even (odd) parity of the input array, the transform outputs have even (odd) parity.
They are therefore called Discrete Cosine Transform (DCT) and Discrete Sine Transfrom (DST), respectively.
The logical size of the corresponding DFT is denoted as N.
The actual array size given to FFTW is denoted by n.
For the DCT/DST types implemented in FFTW, N is always even.
Note that this does not pose any restrictions on the input array sizes n.
One can think of the logical DFT input array as one that FFTW 'sees' internally and computes a regular DFT of.
The resulting output array is purely real and features the named symmetry properties,
since the logical input array was 'constructed' from the given input array to have the desired symmetry properties.
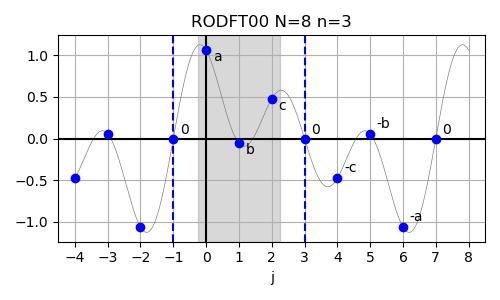
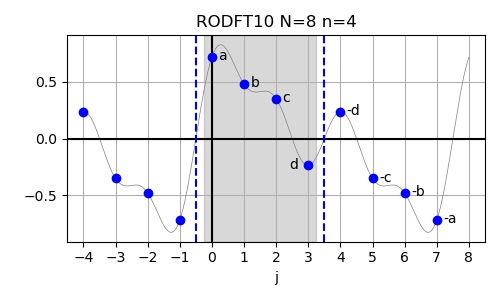
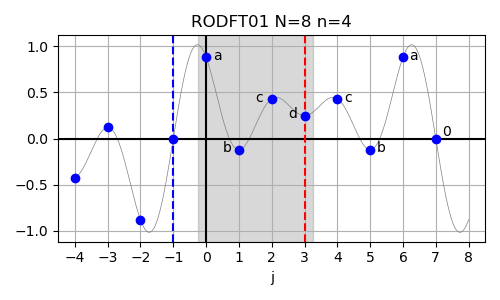
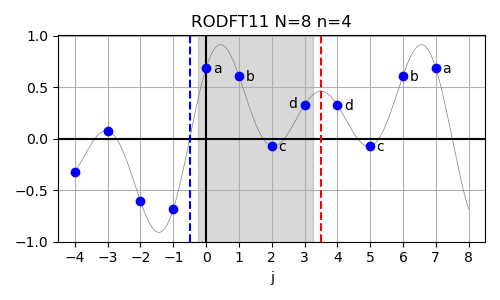
In below example plots used to illustrate these symmetry properties/assumptions, random Fourier coefficients have been sampled and transformed back to real-space using the named inverse transforms. This allows to 'evaluate' the input data also in the samples given in the (small) input arrays. In these plots, red dashed vertical lines indicate even symmetry (f(x)=f(-x)) about the indicated position and blue dashed vertical lines indicate odd symmetry (f(x)=-f(-x)) about the indicated position. The grey-shaded area in the background indicated the range of samples that are included in the input array. The x axis labels denote the indices in the actual input array given to FFTW (only valid within the range of the grey boxes).
The nomenclature works as follows: The first letter is R to indicate real-valued data. The second letter distinguished between E for even-parity data and O for odd-parity data. The following DFT is for discrete Fourier transform (who guessed...). The next two digits indicate wheter (1) or not (0) the input (first digit) or the output (second digit) data is 'shifted' by half a sample. Think of this in terms of parity: whether the symmetry axis is located at a sample (no shifting necessary) or between two samples (shifting necessary). The shifting becomes necessary when formulating the symmetry properties over sampled data that has integer indices vs. symmetry axis that are possibly located at half-integer locations.
For all transforms, a periodicity of N is assumed for the logical input array as X_j = X_{N+j} where X is the input data array.
Here is a quick overview table to indicate the assumed symmetries in the input array for the following types of r2r DFTs:
| type | actual r2r input |
logically-equivalent DFT input |
|---|---|---|
| REDFT00 | a b c d e |
a b c d e d c b |
| REDFT10 | a b c d |
a b c d d c b a |
| REDFT01 | a b c d |
a b c d 0 -d -c -b |
| REDFT11 | a b c d |
a b c d -d -c -b -a |
| RODFT00 | a b c |
0 a b c 0 -c -b -a |
| RODFT10 | a b c d |
a b c d -d -c -b -a |
| RODFT01 | a b c d |
a b c d c b a 0 |
| RODFT11 | a b c d |
a b c d d c b a |
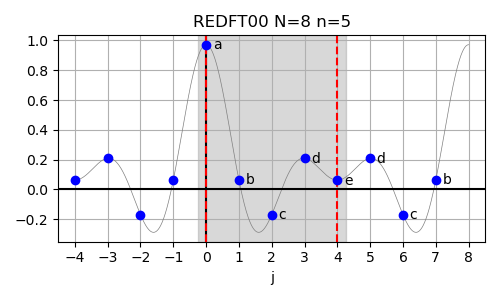
In case of the real-valued even-parity DFT with no shifts in either input or output array (REDFT00),
also called the DCT-I, the corresponding logical DFT size is given by N = 2(n-1), corresponding to n = N/2+1.
The formal definition of the REDFT00 is given below:
The inverse of this transform is REDFT00 itself. The input array is assumed to have even symmetry around j=0 and even symmetry also around j=n−1.
In above figure, the lowercase letters a to e refer to the input data abcde for the size-5 REDFT00, which is logically equivalent to a size-8 DFT with real-valued input data abcdedcb.
In order to demonstrate the use of this method,
the logically equivalent DFT input is filled appropriately and its output is checked against REDFT00.
In the following code, in is the input array (size n) given to REDFT00
and in_logical is the (complex-valued) input array (size N) handed to a generic 1D DFT.
Similarly, out is the output array (size n) from REDFT00
and out_logical is the output array (size N) from a generic 1D DFT.
Here is how the symmetric input is generated:
// the first half of the array is identical
for (int i=0; i<n; ++i) {
in_logical[i] = in[i];
}
// second half is filled according to even symmetry around n-1
for (int i=0; i<n-1; ++i) {
in_logical[n+i] = in[n-2-i];
}The checks are a little bit more involved, but managable:
// 1. logically equivalent output should be purely real-valued
for (int i = 0; i < N; ++i) {
if (fabs(cimag(out_logical[i])) > eps) {
printf("error: imag of [%d] is %g\n", i, cimag(out_logical[i]));
status = 1;
} else {
printf("imag of [%d] is %g\n", i, cimag(out_logical[i]));
}
}
// 2. first n values should have identical real values
double delta;
for (int i = 0; i < n; ++i) {
delta = out_logical[i] - out[i];
if (fabs(delta) > eps) {
printf("error: delta of [%d] is %g\n", i, delta);
status = 1;
} else {
printf("match of [%d] (delta=%g)\n", i, delta);
}
}
// 3. even symmetry of output values around n-1
for (int i = 0; i < n - 2; ++i) {
delta = out_logical[n + i] - out[n - 2 - i];
if (fabs(delta) > eps) {
printf("error: delta of [%d] is %g\n", n+i, delta);
status = 1;
} else {
printf("match of [%d] (delta=%g)\n", n+i, delta);
}
}The full example can be found in src/test_1d_redft00.c.
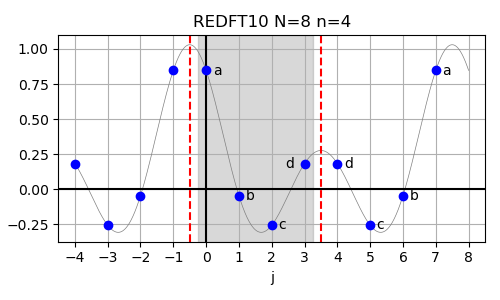
In case of the real-valued even-parity DFT with shifted input data (REDFT10),
also called the DCT-II, the corresponding logical DFT size is given by N = 2n, corresponding to n = N/2.
This function is commonly known as "the" DCT.
The formal definition of the REDFT10 is given below:
The inverse of this transform is REDFT01. The input array is assumed to have even symmetry around j=-0.5 and even symmetry also around j=n−0.5.
In above figure, the lowercase letters a to e refer to the input data abcd for the size-4 REDFT10, which is logically equivalent to a size-8 DFT with real-valued input data abcddcba.
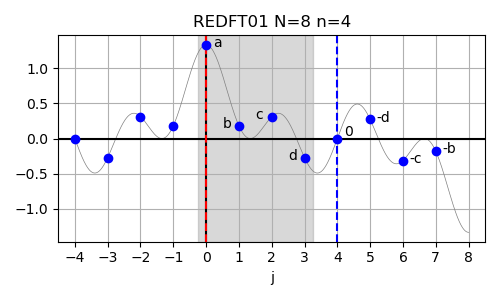
In case of the real-valued even-parity DFT with shifted output data (REDFT01),
also called the DCT-III, the corresponding logical DFT size is given by N = 2n, corresponding to n = N/2.
This function is commonly known as "the" inverse DCT (IDCT).
The formal definition of the REDFT01 is given below:
The inverse of this transform is REDFT10. The input array is assumed to have even symmetry around j=0 and odd symmetry around j=n.
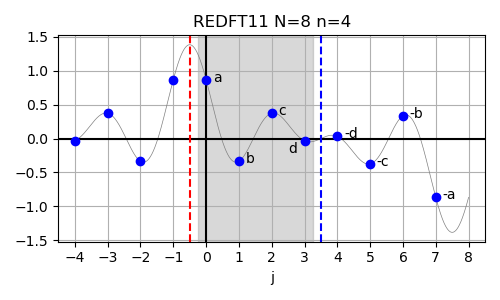
In case of the real-valued even-parity DFT with both shifted input and output data (REDFT11),
also called the DCT-IV, the corresponding logical DFT size is given by N = 2n, corresponding to n = N/2.
The formal definition of the REDFT11 is given below:
The inverse of this transform is REDFT11 itself. The input array is assumed to have even symmetry around j=-0.5 and odd symmetry around j=n-0.5.
For the DCTs, also consider https://en.wikipedia.org/wiki/Discrete_cosine_transform#Formal_definition and in particular https://upload.wikimedia.org/wikipedia/commons/a/ae/DCT-symmetries.svg .
In case of the real-valued odd-parity DFT with no shifts in either input or output array (RODFT00),
also called the DST-I, the corresponding logical DFT size is given by N = 2(n+1), corresponding to n = N/2-1.
Note that the periodicity of N of the logical input array in combination with odd symmetry X_j = -X_{n-j}
leads to X_0 = -X_0 which is equivalent to X_0 = 0.
This first always-zero element of the input array is not explicitly included in the input to FFTW
and the input array thus has a size of one less and the indices of the symmetry axis shift by 1.
The formal definition of the RODFT00 is given below:
The inverse of this transform is RODFT00 itself. The input array is assumed to have odd symmetry around j=-1 and odd symmetry also around j=n.
In case of the real-valued odd-parity DFT with shifted input data (RODFT10),
also called the DST-II, the corresponding logical DFT size is given by N = 2n, corresponding to n = N/2.
This function is commonly known as "the" DST.
The formal definition of the RODFT10 is given below:
The inverse of this transform is RODFT01. The input array is assumed to have odd symmetry around j=-0.5 and odd symmetry also around j=n-0.5.
In case of the real-valued odd-parity DFT with shifted output data (RODFT01),
also called the DST-III, the corresponding logical DFT size is given by N = 2n, corresponding to n = N/2.
This function is commonly known as "the" inverse DST (IDST).
The formal definition of the RODFT01 is given below:
The inverse of this transform is RODFT10. The input array is assumed to have odd symmetry around j=-1 and even symmetry around j=n-1.
In case of the real-valued odd-parity DFT with both shifted input and output data (RODFT11),
also called the DST-IV, the corresponding logical DFT size is given by N = 2n, corresponding to n = N/2.
The formal definition of the RODFT11 is given below:
The inverse of this transform is RODFT11 itself. The input array is assumed to have odd symmetry around j=-0.5 and even symmetry around j=n-0.5.
For the DSTs, consider also https://en.wikipedia.org/wiki/Discrete_sine_transform#Definition and in particular https://upload.wikimedia.org/wikipedia/commons/3/31/DST-symmetries.svg .
Throughout this example collection, the proposed convenience wrapper functions provided by FFTW for allocating real- and complex-valued arrays are used:
int n = 32;
int nOut = n/2+1;
double *in = fftw_alloc_real(n);
fftw_complex *out = fftw_alloc_complex(nOut);where N is the real-space size of the DFT and outN is the number of Fourier coefficients resulting from a r2c DFT.
The corresponding "raw" allocation code would look like this:
double *in = (double*) fftw_malloc(sizeof(double) * n);
fftw_complex *out = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * nOut);Note that above code is equivalent to the standard C way of allocating memory using malloc:
double *in = (double*) malloc(sizeof(double) * n);
fftw_complex *out = (fftw_complex*) malloc(sizeof(fftw_complex) * nOut);except that the FFTW routines ensure proper memory alignment for exploiting SIMD instructions of modern CPUs.
In order to keep the examples short, a separate header file src/util.h is provided.
It contains methods to operate on one- and two-dimensional arrays (the latter stored in row-major order)
of real (double) and complex (fftw_complex) numbers.
The following operations are supported:
- fill with random numbers between 0 and 1: e.g.
fill_random_1d_cplx - element-wise check for approximate equality: e.g.
compare_1d_real - write into a text file: e.g.
dump_1d_real