The best way to make sure that your GME computation is converged is to increase the parameters controlling the precision of the simulation until you no longer see change in the eigenmodes of interest. We recommend doing this in the following order:
- First, make sure you have set a high enough
gmax, which is defined upon initialization ofGuidedModeExp. - Then, increase the number of guided bands included in the simulation by
adding more indexes to the
gmode_indslist supplied to :meth:`legume.GuidedModeExp.run`. Note that after including more modes ingmode_inds, you should test again the convergence w.r.t.gmax. - If your bands look particularly weird and discontinuous, there might be an
issue in the computation of the guided modes of the effective homogeneous
structure (the expansion basis). Try decreasing
gmode_stepsupplied in :meth:`legume.GuidedModeExp.run` to1e-3or1e-4and see if things look better.
Finally, note that GME is only an approximate method. So, even if the simulation is converged with respect to all of the above parameters but still produces strange results, it might just be that the method is not that well-suited for the structure you are simulating. We're hoping to improve that in future version of legume!
The Fourier expansion of electromagnetic fields relies on an infinite vector set G as its basis. However, for practical numerical computations, it becomes necessary to truncate this infinite basis. The choice of the truncation rule becomes crucial, as the results may vary for a finite number (NG) of plane waves. It is expected that all reasonable truncation choices converge to the same result as NG approaches infinity. In legume, two distinct truncation rules are implemented:
abs: This rule defines a circular boundary in reciprocal space with the condition|G| < 2 π gmax;tbt: This creates a parallelogram in reciprocal space, which is suitable to put the dielectric matrices in Toeplitz-block-Toeplitz form.
In both case, the number (NG) of plane waves (sometimes called npw in the code) grows like the square of gmax.
An illustrative example of these truncation rules applied to the reciprocal triangular lattice is shown here, where the darker points corresponds to vectors G included in the basis:
Caution!
For given gmax, abs and tbt may give a different number of
plane waves NG in the basis.
So, should I use abs or tbt? abs is, in general, a safer choice since it
always preserves the underlying symmetry of any lattice. In particular, abs should
be chosen when using symmetrization with respect to a vertical mirror plane in the hexagonal (also called triangular) lattice.
From the plot above, we can see that tbt breaks the rotational symmetry of the hexagonal lattice,
and is therefore not compatible with symmetrization. Also, tbt may give
unexpected results when the symmetry of the modes is a crucial point of the simulation.
On the other hand, the calculation of the Fourier components of the in-plane dielectric
profile is highly optimized for the tbt truncation. For this reason, when
we need to run a calculation with a large number of plane waves,
tbt is currently the best option in terms of computing time and memory usage.
Inverse design optimizations are often done with a rectangular supercell, and for
such structures tbt is compatible with symmetrization.
Note
Based on these guidelines, the user should choose the truncation scheme that is most
suited to the specific application. The choice of truncation scheme depends on the
keyword argument truncate_g in GuidedModeExp, and has the default value abs.
GME requrest the diagonalization of dense matrices, and you might start running
out of memory for simulations in which computational time is not that much of
an issue. This is also because the scaling with gmax is pretty bad: the
linear dimension of the matrix for diagonalization scales as gmax**2,
and so the total memory needed to store it scales as gmax**4. You can improve
the memory usage a bit by using the eigsh solver to only compute a few eigenmodes
as discussed in the next question. But things get even
worse in gradient computations. Reverse-mode autodiff is generally the best
approach for optimization problems in terms of computational time, but this can
sometimes come at a memory cost. This is because all of the intermediate
values of the forward simulation have to be stored for the backward pass.
So, if you are for example doing a loop through different k-points, the dense
matrices and their eigenvectors at every k will be stored, which can add up
to a lot. There is no easy way to fix this (and no direct way within
autograd), but we've included a function that can provide a workaround.
For details on things you can try, have a look at this example.
Finally, it's worth mentioning that there are probably improvements that can be made to the memory usage. If anybody wants to dive deep in the code and try to do that, it will be appreciated! I have pointed out some ideas along these lines here.
The options that can be supplied in :meth:`legume.GuidedModeExp.run` include
numeig and eig_sigma, which define that numeig eigenmodes
closest to eig_sigma are to be computed. However, note that the default solver
defined by the eig_solver option is numpy.linalg.eigh, which always computes
all modes. Thus, numeig in this case only defines the number of
modes which will be stored, but it does not affect performance. If you're
looking for a small number of eigenvalues, you can try setting eig_solver = eigsh,
which will use the scipy.sparse.linalg.eigsh method. In some cases this
will be faster, so it's worth a try -- but it might also not be, since the matrix for
diagonalization is dense, and this is why it is not the default option. Have a
look at this example for usage.
In some simulations, the computation of the radiative losses could be the time
bottleneck. In some cases, e.g. when optimizing a cavity, you only need to
compute the quality factor of a single mode. If you run the GME by default,
the Q-s of all modes will be computed instead, but you can set the option
compute_im = False to avoid this. Running the GME with this option will
compute all modes, but not the imaginary part of their frequencies (which is
done perturbatively after the first stage of the computation). Then, you can
use the :meth:`legume.GuidedModeExp.compute_rad` method to only compute the loss rates
of selected modes.
The expansion basis in the GME consists of the guided modes of an effective
homogeneous structure (panels (a)-(b)) in the Figure. By default, the
effective permittivities in (b) are taken as the average value in every layer.
This is controlled by the gmode_eps keyword option in the run options.
Setting gmode_eps = 'background' will take the background permittivity
instead, while there's also the option to have custom values by setting
gmode_eps = 'custom'. In that case, every layer (including the claddings)
in the PhotCryst object should have a pre-defined effective permittivity
eps_eff, which will be used in the guided-mode computation. This is simply
set as an attribute of the layer, e.g.
phc.layers[0].eps_eff = 10 # Slab custom effective epsilon
phc.calddings[0].eps_eff = 1 # Lower cladding
phc.claddings[1].eps_eff = 5 # Upper claddingThe guided modes can be classified as TE/TM, where in our notation the reference
plane is the slab plane (xy). The guided modes alternate between TE and TM, such
that gmode_inds = [0, 2, 4, ...] are TE and gmode_inds = [1, 3, 5, ...]
are TM (panel (c)). However, this classification is often broken by the
photonic crystal structure (we discuss symmetries further below).
We only include the fully-guided modes in the computation (the ones that lie below both light lines in (c)). This is what makes the computation approximate, as the basis set is not complete.
The TE/TM classification of the guided modes of the homogeneous structure is often broken by the photonic crystal permittivity. Here is how you can still incorporate some structural symmetries.
For gratings (permittivity is periodic in one direction and homogeneous in the other), the TE/TM classification holds. You can selectively compute the modes by supplying gmode_inds with either only even or only odd numbers. Please see example 0.2 for other hints.
For 2D structures, it is most important to distinguish between horizontal (xy) and vertical (kz) mirror planes, that latter may arise only if the k-vector points along specific high-symmetry directions.
For photonic crystals with a horizontal (xy) mirror plane, like a single slab with symmetric claddings, the correct classification of modes is with respect to reflection in that plane:
- the positive-symmetry, or \sigma_{xy}=+1 photonic modes are obtained by choosing a basis of guided modes such as
gmode_inds = [0, 3, 4, 7, 8, 11 ...]; - the negative-symmetry, or \sigma_{xy}=-1 photonic modes are obtained by choosing a basis of guided modes such as
gmode_inds = [1, 2, 5, 6, 9, 10, ...].
Low-frequency positive-symmetry modes that are mostly formed by the gmode_inds = [0]
guided band are sometimes referred to as quasi-TE, and low-frequency negative-symmetry
modes that are mostly formed by the gmode_inds = [1] guided band are
sometimes referred to as quasi-TM. Please see example 1.1 for full analysis.
Without any horizontal mirror planes, all the guided modes are generally mixed.
There can still be symmetry if the k-vector points in a high-symmetry direction.
The new version of legume (2024 version, related to the CPC paper)
allows implementing symmetry with respect to a vertical mirror plane, which
we call a kz-plane. This is controlled by the keyword argument kz_symmetry,
which can have four possible values:
kz_symmetry=None: kz-symmetry is not used;kz_symmetry='even': only kz-even modes are calculated ;kz_symmetry='odd': only kz-odd modes are calculated ;kz_symmetry='both': all modes are calculated, and can be separated using the variable kz_symmetry=kz_symms.
Please see example 1.2 for full analysis, example 1.6 for inverse design using kz-symmetry, and the CPC paper for theoretical discussion.
Polaritons are the mixed modes that result from the interaction of light with material excitation, in this case we consider 2D excitons. To model exciton-polaritons in PhC slabs we need to calculate the exciton eigenmodes, and photonic eigenmodes, and their mutual interaction.
Exciton eigenmodes are obtained by solving the effective-mass equation in a confining potential, using the same plane-wave basis that is employed for the photonic eigenmodes. The exciton-photon interaction is treated by the Hopfield method, which leads to a non-hermitian eigenvalue problem.
The polariton class HopfieldPol is organized in a way that is similar to GuidedModeExp, but it employs SI units and sometimes electronvolts (eV), as the exciton resonances are characterized by real parameters like resonance energy, loss, and oscillator strength per unit area.
Please refer to example 1.5 for details on usage.
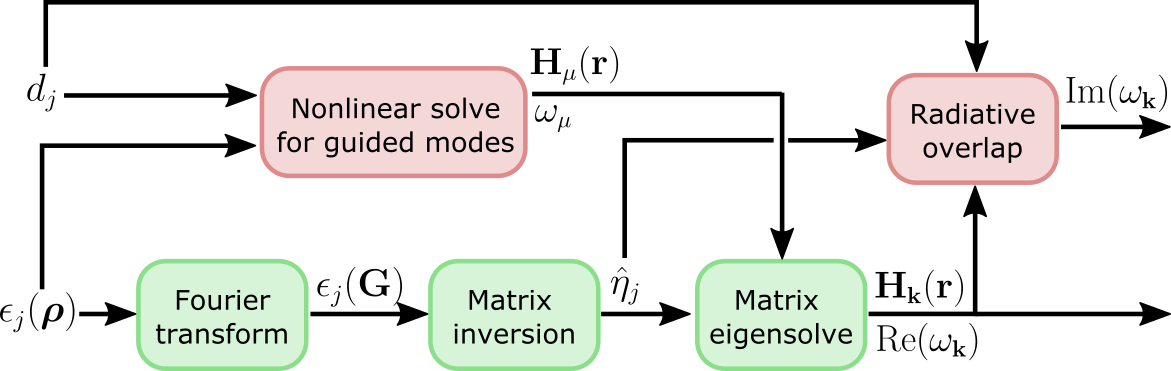
When running GME with the autograd backend, one of the run() options
you can specify is 'gradients' = {'exact' (default), 'approx'}. The
approximate option could be faster in some cases, and could actually still
be exact in some cases. This is the high-level computational graph of the
guided-mode expansion:
The 'approx' option discards the gradient due to the top path in this
graph, i.e. the gradient due to the changing basis. Only the gradient from the
diagonalization path is included. Here are some rules of thumb on what to use:
- If you're optimizing hole positions, or more generally parameters that don't
change the average permittivity, you're in luck! In this case, the
'approx'gradients should actually be exact! - If you're optimizing dispersion (real part of eigenfrequencies), you could try using
'approx'gradients, as they might be within just a few percent of the exact ones. - If you're optimizing loss rates or field profiles
and/or if your parameters include the layer thicknesses, then the
'approx'gradients could be significantly off,'exact'is recommended (and is the default).
Something to be aware of is the fact that the eigenmodes come with an arbitrary k-dependent gauge, as is usually the case for eigenvalue simulations. That is to say, each eigenvector is defined only up to a global phase, and this phase might change discontinously even for nearby k-points. If you re looking into something that depends on the gauge choice, you will have to figure out how to set your preferred gauge yourself.
Of course, apart from this global phase, all the relative phases should be well-defined (as they correspond to physically observable quantities). So for example if you compute radiative couplings to S and P polarization, the relative phase between the two should be physical.
The 2020 paper gives the fundamentals on the guided-mode expansion method and on our differentiable implementation.
The 2024 paper gives basic theory and details on symmetrization with respect to a vertical mirror plane, and on the interaction of photonic modes with excitons leading to photonic crystal polaritons.
If you find legume useful for your research, we would apprecite you citing our paper. For your convenience, you can use the following BibTex entry:
@article{Minkov2020,
title = {Inverse Design of Photonic Crystals through Automatic Differentiation},
volume = {7},
ISSN = {2330-4022},
url = {https://dx.doi.org/10.1021/acsphotonics.0c00327},
DOI = {10.1021/acsphotonics.0c00327},
number = {7},
journal = {ACS Photonics},
publisher = {American Chemical Society (ACS)},
author = {Minkov, Momchil and Williamson, Ian A. D. and Andreani, Lucio C. and Gerace, Dario and Lou, Beicheng and Song, Alex Y. and Hughes, Tyler W. and Fan, Shanhui},
year = {2020},
month = jun,
pages = {1729–1741}
}The paper describing the symmetry separation and polariton theory has been published in CPC. If you find the new features useful, please cite our paper using the following BibTex entry:
@article{Zanotti2024legume,
title = {Legume: A free implementation of the guided-mode expansion method for photonic crystal slabs},
journal = {Computer Physics Communications},
volume = {304},
pages = {109286},
year = {2024},
issn = {0010-4655},
doi = {https://doi.org/10.1016/j.cpc.2024.109286},
url = {https://www.sciencedirect.com/science/article/pii/S0010465524002091},
author = {Simone Zanotti and Momchil Minkov and Davide Nigro and Dario Gerace and Shanhui Fan and Lucio Claudio Andreani},
}The legume logo was designed by Nadine Gilmer. She is also behind the logos for our angler and ceviche packages.