Skip to content

Latest commit

 

History

History
951 lines (648 loc) · 18.4 KB

digital.mdown

File metadata and controls

951 lines (648 loc) · 18.4 KB
Raw

%Digital Electronics %Diego Trapero

Digital Electronics

Binary

The binary numeral system, or base-2 numeral system, represents numeric values using two symbols: typically 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2. #

$[x]_{10}$ $[x]_{2}$ $[x]_{16}$
0 0000 0
1 0001 1
2 0010 2
3 0011 3
4 0100 4
5 0101 5
6 0110 6
7 0111 7
8 1000 8
9 1001 9
10 1010 A
11 1011 B
12 1100 C
13 1101 D
14 1110 E
15 1111 F

Powers of 2

$n$ $2^n$
0 1
1 2
2 4
3 8
4 16
5 32
6 64
7 128
8 264
9 512
10 1024

Numbers you can represent with $n$ bits

System Range
Natural binary $0$ to $2^n-1$
One's complement $-2^{n-1}-1$ to $2^{n-1}-1$
Two's complement $-2^{n-1}$ to $2^{n-1}-1$

Binary - Decimal Conversion

Binary to Decimal Conversion

Digit weighting

\vspace{50mm}

Decimal to Binary Conversion

Sum of weights

\vspace{50mm}

Repeated division by 2

\vspace{50mm}

Binary Arithmetic

Binary Addition

Addition rules

  • $0 + 0 = 0$
  • $0 + 1 = 1$
  • $1 + 0 = 1$
  • $1 + 1 = 10$ (1 and carry 1)
  1 1 1 1 1    (carried digits)
    0 1 1 0 1
+   1 0 1 1 1
-------------
= 1 0 0 1 0 0 = 36

\vspace{50mm}

Binary Substraction

Substraction rules

  • $0 - 0 = 0$
  • $0 - 1 = 0$
  • $1 - 0 = 1$
  • $10 - 1 = 1$
    *   * * *   (starred columns are borrowed from)
  1 1 0 1 1 1 0
-     1 0 1 1 1
----------------
= 1 0 1 0 1 1 1

\vspace{50mm}

Binary Multiplication

Multiplication rules

  • $0 \cdot 0 = 0$
  • $0 \cdot 1 = 0$
  • $1 \cdot 0 = 0$
  • $1 \cdot 1 = 1$
           1 0 1 1   (A)
         × 1 0 1 0   (B)
         ---------
           0 0 0 0   ← Corresponds to the rightmost 'zero' in B
   +     1 0 1 1     ← Corresponds to the next 'one' in B
   +   0 0 0 0
   + 1 0 1 1
   ---------------
   = 1 1 0 1 1 1 0

               1 0 1 . 1 0 1     A (5.625 in decimal)
             × 1 1 0 . 0 1       B (6.25  in decimal)
             -------------------
                   1 . 0 1 1 0 1   ← Corresponds to a 'one' in B
     +           0 0 . 0 0 0 0     ← Corresponds to a 'zero' in B
     +         0 0 0 . 0 0 0
     +       1 0 1 1 . 0 1
     +     1 0 1 1 0 . 1
     ---------------------------
     =   1 0 0 0 1 1 . 0 0 1 0 1  (35.15625 in decimal)

\vspace{50mm}

Binary Division

\vspace{30mm}

Complements

In mathematics and computing, the method of complements is a technique used to subtract one number from another using only addition of positive numbers. This method was commonly used in mechanical calculators and is still used in modern computers. To subtract a number y (the subtrahend) from another number x (the minuend), the radix complement of y is added to x and the initial '1' of the result is discarded. Discarding the initial '1' is especially convenient on calculators or computers that use a fixed number of digits: there is nowhere for it to go so it is simply lost during the calculation. #

1's Complement

The One's complement of a binary number is defined as the value obtained by inverting all the bits in the binary representation of the number (swapping 0s for 1s and vice-versa). #

The ones' complement of the number then behaves like the negative of the original number in some arithmetic operations, although it presents some problems that are solved by the two's complement, like the offset by -1.

Examples

$$1C[11010] = 00101$$

2's Complement

Obtain the 2's complement

  • From the 1's complement $$2C[x] = 1c[x] + 1$$

  • Working from LSB to MSB

\vspace{50mm}

Signed numbers

Sign-magnitude form \vspace{50mm}

1's complement form \vspace{50mm}

2's complement form \vspace{50mm}

Boolean Algebra

Digital components

Logic Gates

$$ \Tree [.{Logic Gates} [.Basic NOT AND OR ] [.Derived NAND NOR XOR XNOR ] ] $$

  • Basic gates perform the three basic boolean operations: conjunction (AND), disjunction (OR) and negation (NOT). Only one the two other gates is neccesary in conjuntion with the NOT gate to implement everty boolean function. The other operation can be expressed in therms of the other two.
  • Derived gates perform derived boolean operations, operations that can be composed from basic operations. The most common are NAND, NOR, XOR, and XNOR gates.

NOT Gate

$$ \begin{circuitikz} \draw (0,0) nodenot port {} (notGate.in) node[left] {$A$} (notGate.out) node[right] {$\text{NOT } A$} ; \end{circuitikz} $$

Rule: The NOT gate output is the complementary of the input

A NOT A
0 1
1 0

AND Gate

$$ \begin{circuitikz} \draw (0,0) nodeand port {} (andGate.in 1) node[left] {$A$} (andGate.in 2) node[left] {$B$} (andGate.out) node[right] {$A \text{ AND } B$} ; \end{circuitikz} $$

Rule: The AND gate output is 1 only when all the inputs are 1.

A B A AND B
0 0 0
0 1 0
1 0 0
1 1 1

OR Gate

$$ \begin{circuitikz} \draw (0,0) nodeor port {} (orGate.in 1) node[left] {$A$} (orGate.in 2) node[left] {$B$} (orGate.out) node[right] {$A \text{ OR } B$} ; \end{circuitikz} $$

Rule: The OR gate output is 1 when any of the inputs is 1.

A B A OR B
0 0 0
0 1 1
1 0 1
1 1 1

NAND Gate

$$ \begin{circuitikz} \draw (0,0) nodenand port {} (nandGate.in 1) node[left] {$A$} (nandGate.in 2) node[left] {$B$} (nandGate.out) node[right] {$A \text{ NAND } B$} ; \end{circuitikz} $$

Rule: The NAND gate output is 0 when all the inputs are 1

  • The NAND gate is a NOT-AND gate
  • The NAND gate can be viewed as a negative-OR whose output is 1 when any inputs is 0

NOR Gate

$$ \begin{circuitikz} \draw (0,0) nodenor port {} (norGate.in 1) node[left] {$A$} (norGate.in 2) node[left] {$B$} (norGate.out) node[right] {$A \text{ NOR } B$} ; \end{circuitikz} $$

Rule: The NOR gate output is 0 when any of the inputs is 1.

  • The NOR gate is a NOT-OR gate
  • The NOR gate can be viewd as a negative-AND whose output is 1 only when all the inputs are 0.

XOR Gate

$$ \begin{circuitikz} \draw (0,0) nodexor port {} (xorGate.in 1) node[left] {$A$} (xorGate.in 2) node[left] {$B$} (xorGate.out) node[right] {$A \text{ XOR } B$} ; \end{circuitikz} $$

Rule: The XOR gate output is 1 when all the inputs are not the same

XNOR Gate

$$ \begin{circuitikz} \draw (0,0) nodexnor port {} (xnorGate.in 1) node[left] {$A$} (xnorGate.in 2) node[left] {$B$} (xnorGate.out) node[right] {$A \text{ XNOR } B$} ; \end{circuitikz} $$

Rule: The XNOR gate output when the inputs are not the same

Adders

Half adder

$$ \begin{circuitikz} \draw (0, 0) nodehalfAdder {HA} ; \end{circuitikz} $$

A half adder is a two input, two output circuit, that takes two input bits, $A$ and $B$, and ouputs the two-digit sum, $A + B$. The MSB of the sum is referred as C (carry) and the LSB digit is S (sum). If performing addition digit by digit, the $S$ ouput it's the result digit and the $C$ output is the carry resulting of the operation. This adder does't take into account the carry of the previous digit addition, this is why it is called half adder.

Truth table

$A$ $B$ $C$ $S$
0 0 0 0
1 0 0 1
0 1 0 1
1 1 1 0

Logic operations

  • $S = A \oplus B$
  • $C = AB$

Gate implementation

$$ \begin{circuitikz} \draw (4,2) nodexor port {} %xor gate (0,2.25) to[short](xorGate.in 1) %xor A wiring (0,1.75) to[short](xorGate.in 2) %xor B wiring (0,2.25) node[ocirc] {} %A node (0,2.25) node[left] {$A$} %A label (0,1.75) node[ocirc] {} %B node (0,1.75) node[left] {$B$} %B label (xorGate.out) toshort %S output wiring (5,2) node[ocirc] {} %S node (5,2) node[right] {$S$} %S label (4,0) nodeand port {} %AND gate (1,2.25) node[circ] {} (1.5,1.75) node[circ] {} (1.5,1.75) |- (andGate.in 1) (1,2.25) |- (andGate.in 2) (andGate.out) toshort %C output wiring (5,0) node[ocirc] {} %C node (5,0) node[right] {$C$} %C label ; \end{circuitikz} $$

Full adder

$$ \begin{circuitikz} \draw (0, 0) nodefullAdder {} ; \end{circuitikz} $$

A full adder is a three input, two output circuit, that takes three input bits, $A$, $B$ and $C_i$, and ouputs the two-digit sum, $A + B + C_i$. If performing addition digit by digit, $A$ and $B$ are the operands, $C_i$ the previous carry, the $S$ ouput it's the result digit and the $C$ output is the carry resulting of the operation.

Truth table

$A$ $B$ $C_i$ $C_o$ $S$
0 0 0 0 0
1 0 0 0 1
0 1 0 0 1
1 1 0 1 0
0 0 1 0 1
1 0 1 1 0
0 1 1 1 0
1 1 1 1 1

Logic operations

  • $S = A \oplus B \oplus C_i$
  • $C_o = (A \cdot B) + (C_i \cdot (A \oplus B))$

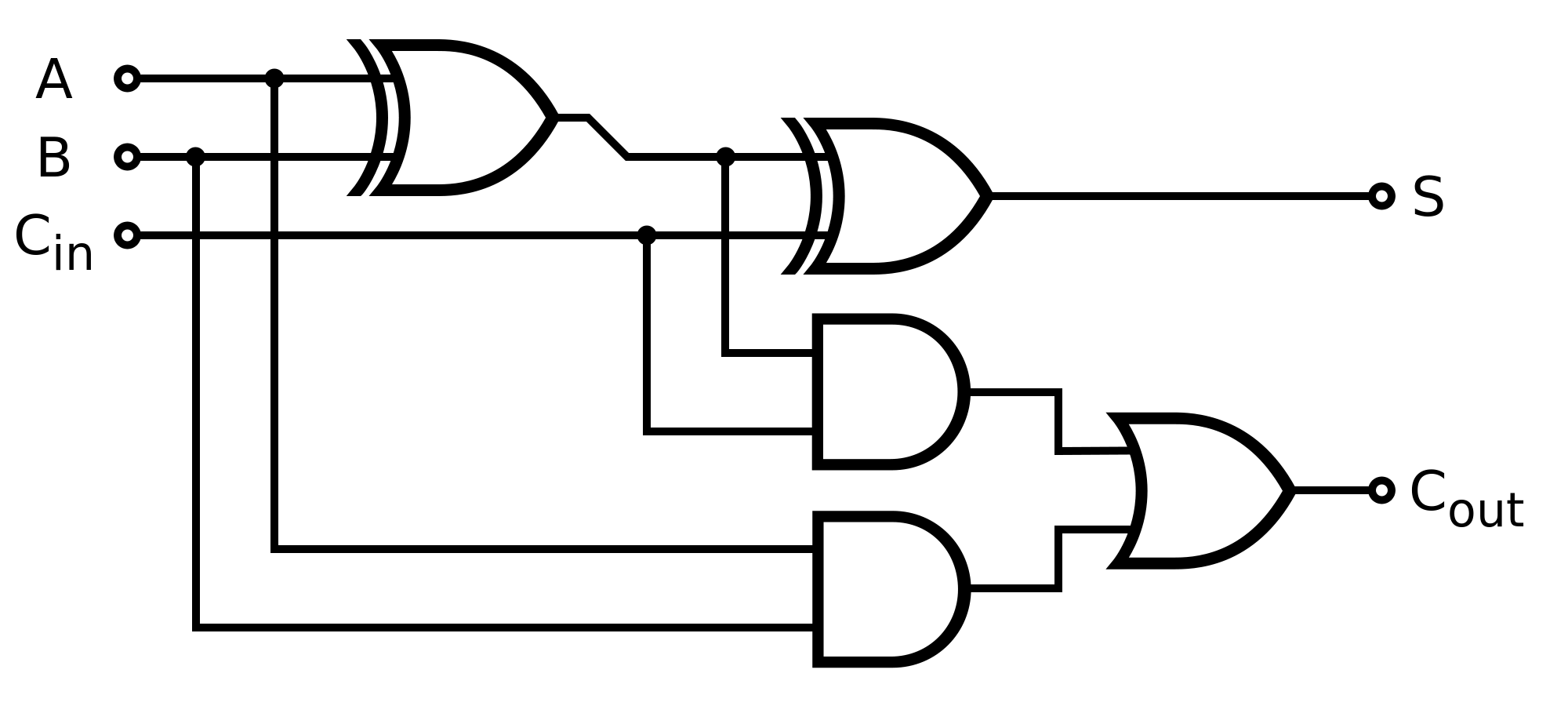
Gate implementation

Source: https://commons.wikimedia.org/wiki/File:Full_Adder.svg

Full adder from two half adders A full adder can be implemented from two half adders and an OR gate:

$$ \begin{circuitikz} %Full adder from two half adders, Diego Trapero \draw (1.2, 0.0) nodehalfAdder {HA1} %HA1 (3.6, 0.0) nodehalfAdder {HA2} %HA2 (0.0, 0.5) nodeocirc {} (0.0, 0.5) node[left] {$A$} (0.0, 0.5) toshort (0.0, -0.5) nodeocirc {} (0.0, -0.5) node[left] {$B$} (0.0, -0.5) toshort (0.0, -1.5) nodeocirc {} (0.0, -1.5) node[left] {$C_i$} (HA1.S) toshort (HA2.S) to[short](6.6, 0.5) (6.0, -1.5) nodeor port {} (6.6, 0.5) nodeocirc {} (6.6, 0.5) node[right] {$S$} (6.6, -1.5) nodeocirc {} (6.6, -1.5) node[right] {$C_o$} (Ci) -| (HA2.B) (HA1.C) |- (OR.in 2) (HA2.C) |- (OR.in 1) (OR.out) -- (Co) ; \end{circuitikz} $$

Comparators

Equality Comparators

1-bit equality comparator A 1 bit equality comparator can be implemented with a XNOR gate:

$$ \begin{circuitikz} \draw (0,0) nodexnor port {} (xnorGate.in 1) node[left] {$A$} (xnorGate.in 2) node[left] {$B$} (xnorGate.out) node[right] {$Y$} ; \end{circuitikz} $$

A B Y
0 0 1
0 1 0
1 0 0
1 1 1

$n$-bit equality comparator A $n$-bit comparator can be implemented by comparing two numbers digit by digit with $n$ XNOR gates and then processing the outputs through an AND gate to check if every bit is the same in the two numbers

Multiplexers, Demultiplexers, Encoders, Decoders

Multiplexer

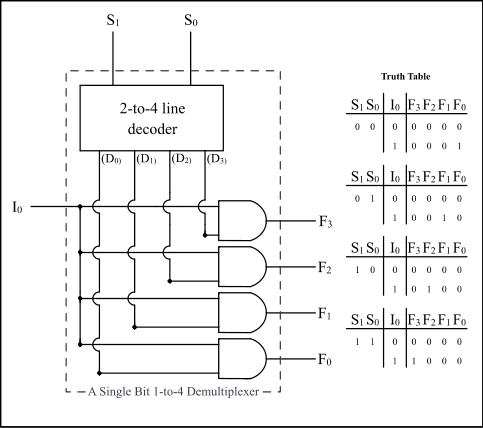
A Multiplexer is...

2 to 1 Multiplexer

$$ \begin{circuitikz} \draw (0,0) node2to1MUX {} ; \end{circuitikz} $$

$$Y = ( D_1 \cdot \overline{S}) + (D_0 \cdot S)$$

$S$ $D_0$ $D_1$ $Y$
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 1
S Y
0 $D_0$
1 $D_1$

A straightforward realization of this 2-to-1 multiplexer would need 2 AND gates, an OR gate, and a NOT gate.

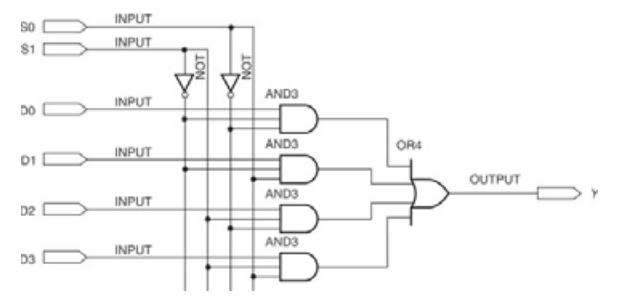
MUX implementation of truth table A mux based circuit can be used to implement a boolean function.

A logic function with $n$ input bits and 1 ouput bit can be implemented in a MUX with $n$ selection bits and $2^n$ data inputs, i.e. a $2^n$-to-1 MUX.

[***** poner ejemplo]

4 to 1 multiplexer. Source: https://www.ecgf.uakron.edu/grover/web/ee263/slides/Chapter%2006B.pdf

Demultiplexer

4 to 1 demultiplexer. Source: https://en.wikipedia.org/wiki/File:Demultiplexer_Example01.svg

Encoder

Decoder

Biestables

Biestables are devices that have two stable states (SET and RESET); they can retain either of these states indefininitly, making them useful as storage devices.

$$ \Tree [.Biestables Latches Flip-Flops ] $$

Latches

Latches are...

$$ \Tree [.Latches {SR Latch} {Gated SR Latch} {Gated D Latch} ] $$

SR (SET-RESET) Latch

$$ \begin{circuitikz} \draw (0, 0) nodesrLatch {SRL} ; \end{circuitikz} $$

Gate implementations

$$ \begin{circuitikz} \draw (0, 1) nodenor port {} (0, -1) nodenor port {} ; \end{circuitikz} $$

Gated SR Latch

$$ \begin{circuitikz} \draw (0, 0) nodegsrLatch {} ; \end{circuitikz} $$

Gated D Latch

$$ \begin{circuitikz} \draw (0, 0) nodegdLatch {} ; \end{circuitikz} $$

Flip-Flops

Flip-flops are...

$$ \Tree [.{Flip-Flops} {SR Flip-Flop} {D Flip-Flop} {JK Flip-Flop} ] $$

$$ \begin{circuitikz} \draw (0, 0) nodesrFlipFlop {} ; \end{circuitikz} $$

D FlipFlop

$$ \begin{circuitikz} \draw (0, 0) nodedFlipFlop {} ; \end{circuitikz} $$

$$ \begin{circuitikz} \draw (0, 0) nodedFlipFlop2x2 {} ; \end{circuitikz} $$

$CLK$ $D$ $Q_{next}$
^ 0 0
^ 1 1
0 X Q
1 X Q

JK FlipFlop

$$ \begin{circuitikz} \draw (0, 0) nodejkFlipFlop {} ; \end{circuitikz} $$

Finite State Machines

Finite State Machines (FSM) are...

  • Moore machine: The FSM uses only entry actions, i.e., output depends only on the state.
  • Mealy machine: The FSM uses only input actions, i.e., output depends on input and state.

Lookup tables

A Lookup Table (LUT) can enconde a $n$-bit boolean function, with 1 bit output.

A $n$-bit LUT can be implemented with a mux whose select lines are the $n$ inputs of the LUT and whose $2^n$ inputs are constants.

2-bit LUT

$X_0$ $X_1$ $Y$
0 0 $y_0$
0 1 $y_1$
1 0 $y_2$
1 1 $y_3$

FPGA logic cell FPGAs are built of many interconnected logic cells. A basic logic cell could be composed of a 4 LUT, a flipflop and a 2to1 mux to bypass the register.

$$ \begin{circuitikz} \draw (2,0) nodejkFlipFlop {$4LUT$} (5,-0.5) nodedFlipFlop2x2 {} (7,0) node2to1MUX {} (LUT.Q) -| (MUX.D0) (LUT.Q) -| (DFF.D) (DFF.Q) -| (MUX.D1) (0, 1) nodeocirc{} (0, 0.5) nodeocirc{} (0, 0) nodeocirc{} (0, -0.5) nodeocirc{} (0, -2.5) nodeocirc{} (0, -2) nodeocirc{} (S) -| (MUX.S) (CLK) -| (DFF.C) ; \end{circuitikz} $$

\newpage

Reference tables

\newpage

Logic Gates

\tabulinesep=1mm \begin{longtabu} to\linewidth{|X[1,m,c]|X[1,m,c]|X[2,m,c]|X[2,m,c]|}

\hline
Gate & Symbol & Rule & Truth table \\
\hline

NOT
& 
\begin{circuitikz} \draw (0,0) node[not port](notGate) {}; \end{circuitikz}
&
The NOT gate output is the complementary of the input
&
not
\\
\hline

AND
&
\begin{circuitikz} \draw (0,0) node[and port](andGate) {}; \end{circuitikz}
&
The AND gate output is 1 only when all the inputs are 1
&
and
\\
\hline

OR
&
\begin{circuitikz} \draw (0,0) node[or port](orGate) {}; \end{circuitikz}
&
The OR gate output is 1 when any of the inputs is 1
&
or
\\
\hline

NAND
&
\begin{circuitikz} \draw (0,0) node[nand port](nandGate) {}; \end{circuitikz}
&
The NAND gate output is 0 when all the inputs are 1
&
or
\\
\hline

NOR
&
NOR
\begin{circuitikz} \draw (0,0) node[nor port](norGate) {}; \end{circuitikz}
&
The NOR gate output is 0 when any of the inputs is 1
&
or
\\
\hline

XOR
&
\begin{circuitikz} \draw (0,0) node[xor port](xorGate) {}; \end{circuitikz}
&
The XOR gate output is 1 when all the inputs are not the same
&
or
\\
\hline

XNOR
&
\begin{circuitikz} \draw (0,0) node[xnor port](xnorGate) {}; \end{circuitikz}
&
The XNOR gate output when the inputs are not the same
&
or
\\
\hline

\end{longtabu}

\newpage

Biestables

$$ \Tree [.Biestables [.Latches {SR Latch} {Gated SR Latch} {Gated D Latch} ] [.{Flip-Flops} {SR Flip-Flop} {D Flip-Flop} {JK Flip-Flop} ] ] $$

\tabulinesep=1mm \begin{longtabu} to\linewidth{X[1,m,c]X[1,m,c]}

\hline
Latch & asd \\
\hline

\begin{circuitikz} \draw (0,0) node[srLatch](notGate) {}; \end{circuitikz}
&
q
\\
\hline

\begin{circuitikz} \draw (0,0) node[gsrLatch](notGate) {}; \end{circuitikz}
&
q
\\
\hline

\begin{circuitikz} \draw (0,0) node[gdLatch](notGate) {}; \end{circuitikz}
&
q
\\
\hline

\end{longtabu}

\tabulinesep=1mm \begin{longtabu} to\linewidth{X[1,m,c]X[1,m,c]}

\hline
FlipFlop & asd \\
\hline

\begin{circuitikz} \draw (0,0) node[srFlipFlop](notGate) {}; \end{circuitikz}
&
q
\\
\hline

\begin{circuitikz} \draw (0,0) node[dFlipFlop](notGate) {}; \end{circuitikz}
&
q
\\
\hline

\begin{circuitikz} \draw (0,0) node[jkFlipFlop](notGate) {}; \end{circuitikz}
&
q
\\
\hline

\end{longtabu}

\newpage

Bibliography

More