全面解析并实现逻辑回归(Python)

[aialgorithm]

本文以模型、学习目标、优化算法的角度解析逻辑回归(LR)模型，并以Python从头实现LR训练及预测。

一、逻辑回归模型结构

逻辑回归是一种广义线性的分类模型且其模型结构可以视为单层的神经网络，由一层输入层、一层仅带有一个sigmoid激活函数的神经元的输出层组成，而无隐藏层。其模型的功能可以简化成两步，“通过模型权重[w]对输入特征[x]线性求和+sigmoid激活输出概率”。具体来说，我们输入数据特征x，乘以一一对应的模型权重w后求和，通过输出层神经元激活函数σ（sigmoid函数）将（wx + b)的计算后非线性转换为0~1区间的概率数值后输出。学习训练（优化模型权重）的过程是通过梯度下降学到合适的模型权重[W]，使得模型输出值Y=sigmoid(wx + b)与实际值y的误差最小。

附注：sigmoid函数是一个s形的曲线，它的输出值在[0, 1]之间，在远离0的地方函数的值会很快接近0或1。对于sigmoid输出作为概率的合理性，可以参照如下证明：

逻辑回归是一种判别模型，为直接对条件概率P(y|x)建模，假设P(x|y)是高斯分布，P(y)是多项式分布，如果我们考虑二分类问题，通过公式变换可以得到：

可以看到，逻辑回归(或称为对数几率回归)的输出概率和sigmoid形式是一致的。

逻辑回归模型本质上属于广义线性分类器（决策边界为线性）。这点可以从逻辑回归模型的决策函数看出，决策函数Y=sigmoid(wx + b)，当wx+b>0，Y>0.5;当wx+b<0，Y<0.5，以wx+b这条线可以区分开Y=0或1（如下图），可见决策边界是线性的。

二、学习目标

逻辑回归是一个经典的分类模型，对于模型预测我们的目标是：预测的概率与实际正负样本的标签是对应的，Sigmoid 函数的输出表示当前样本标签为 1 的概率，y^可以表示为

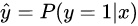
当前样本预测为0的概率可以表示为1-y^

对于正样本y=1，我们期望预测概率尽量趋近为1 。对于负样本y=0，期望预测概率尽量都趋近为0。也就是，我们希望预测的概率使得下式的概率最大（最大似然法）

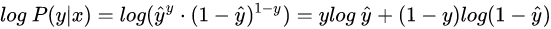
我们对 P(y|x) 引入 log 函数，因为 log 运算并不会影响函数本身的单调性。则有：

我们希望 log P(y|x) 越大越好，反过来，只要 log P(y|x) 的负值 -log P(y|x) 越小就行了。那我们就可以引入损失函数，且令 Loss = -log P(y|x)，得到损失函数为：

我们已经推导出了单个样本的损失函数，是如果是计算 m 个样本的平均的损失函数，只要将 m 个 Loss 叠累加取平均就可以了：

这就在最大似然法推导出的lr的学习目标——交叉熵损失（或对数损失函数），也就是让最大化使模型预测概率服从真实值的分布，预测概率的分布离真实分布越近，模型越好。可以关注到一个点，如上式逻辑回归在交叉熵为目标以sigmoid输出的预测概率，概率值只能尽量趋近0或1，同理loss也并不会为0。

三、优化算法

我们以极小交叉熵为学习目标，下面要做的就是，使用优化算法去优化参数以达到这个目标。由于最大似然估计下逻辑回归没有（最优）解析解，我们常用梯度下降算法，经过多次迭代，最终学习到的参数也就是较优的数值解。
梯度下降算法可以直观理解成一个下山的方法，将损失函数J(w)比喻成一座山，我们的目标是到达这座山的山脚（即求解出最优模型参数w使得损失函数为最小值）。

下山要做的无非就是“往下坡的方向走，走一步算一步”，而在损失函数这座山上，每一位置的下坡的方向也就是它的负梯度方向（直白点，也就是山的斜向下的方向）。在每往下走一步（步长由α控制）到一个位置的时候，求解当前位置的梯度，向这一步所在位置沿着最陡峭最易下山的位置再走一步。这样一步步地走下去，一直走到觉得我们已经到了山脚。
当然这样走下去，有可能我们不是走到山脚（全局最优，Global cost minimun），而是到了某一个的小山谷（局部最优，Local cost minimun），这也梯度下降算法的可进一步优化的地方。
对应的算法步骤：

另外的，以非极大似然估计角度，去求解逻辑回归（最优）解析解，可见kexue.fm/archives/8578

四、Python实现逻辑回归

本项目的数据集为癌细胞分类数据。基于Python的numpy库实现逻辑回归模型，定义目标函数为交叉熵，使用梯度下降迭代优化模型，并验证分类效果：

# coding: utf-8

import numpy as np 
import matplotlib.pyplot as plt
import h5py
import scipy
from sklearn import datasets

# 加载数据并简单划分为训练集/测试集
def load_dataset():
    dataset = datasets.load_breast_cancer()  
    train_x,train_y = dataset['data'][0:400], dataset['target'][0:400]
    test_x, test_y = dataset['data'][400:-1], dataset['target'][400:-1]
    return train_x, train_y, test_x, test_y

# logit激活函数
def sigmoid(z):
    s = 1 / (1 + np.exp(-z))    
    return s
    
# 权重初始化0
def initialize_with_zeros(dim):
    w = np.zeros((dim, 1))
    b = 0
    assert(w.shape == (dim, 1))
    assert(isinstance(b, float) or isinstance(b, int))
    return w, b

# 定义学习的目标函数，计算梯度
def propagate(w, b, X, Y):
    m = X.shape[1]      
    A = sigmoid(np.dot(w.T, X) + b)         # 逻辑回归输出预测值  
    cost = -1 / m *  np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))   # 交叉熵损失为目标函数
    dw = 1 / m * np.dot(X, (A - Y).T)   # 计算权重w梯度
    db = 1 / m * np.sum(A - Y)   
    assert(dw.shape == w.shape)
    assert(db.dtype == float)
    cost = np.squeeze(cost)
    assert(cost.shape == ())    
    grads = {"dw": dw,
             "db": db}    
    return grads, cost

# 定义优化算法
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost):
    costs = []    
    for i in range(num_iterations):    # 梯度下降迭代优化
        grads, cost = propagate(w, b, X, Y)
        dw = grads["dw"]              # 权重w梯度
        db = grads["db"]
        w = w - learning_rate * dw   # 按学习率(learning_rate)负梯度(dw)方向更新w
        b = b - learning_rate * db
        if i % 50 == 0:
            costs.append(cost)
        if print_cost and i % 100 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
    params = {"w": w,
              "b": b}
    grads = {"dw": dw,
             "db": db}
    return params, grads, costs

#传入优化后的模型参数w，b，模型预测   
def predict(w, b, X):
	m = X.shape[1]
	Y_prediction = np.zeros((1,m))
	A = sigmoid(np.dot(w.T, X) + b)
	for i in range(A.shape[1]):
		if A[0, i] <= 0.5:
			Y_prediction[0, i] = 0
		else:
			Y_prediction[0, i] = 1
	assert(Y_prediction.shape == (1, m))
	return Y_prediction

def model(X_train, Y_train, X_test, Y_test, num_iterations, learning_rate, print_cost):
    # 初始化
    w, b = initialize_with_zeros(X_train.shape[0]) 
    # 梯度下降优化模型参数
    parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
    w = parameters["w"]
    b = parameters["b"]
    # 模型预测结果
    Y_prediction_test = predict(w, b, X_test)
    Y_prediction_train = predict(w, b, X_train)
    # 模型评估准确率
    print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
    print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))    
    d = {"costs": costs,
         "Y_prediction_test": Y_prediction_test, 
         "Y_prediction_train" : Y_prediction_train, 
         "w" : w, 
         "b" : b,
         "learning_rate" : learning_rate,
         "num_iterations": num_iterations}    
    return d
    
# 加载癌细胞数据集
train_set_x, train_set_y, test_set_x, test_set_y = load_dataset()   

# reshape
train_set_x = train_set_x.reshape(train_set_x.shape[0], -1).T
test_set_x = test_set_x.reshape(test_set_x.shape[0], -1).T

print(train_set_x.shape)
print(test_set_x.shape)

#训练模型并评估准确率
paras = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 100, learning_rate = 0.001, print_cost = False)

（END）

文章首发公众号“算法进阶”，阅读原文可访问文章相关代码