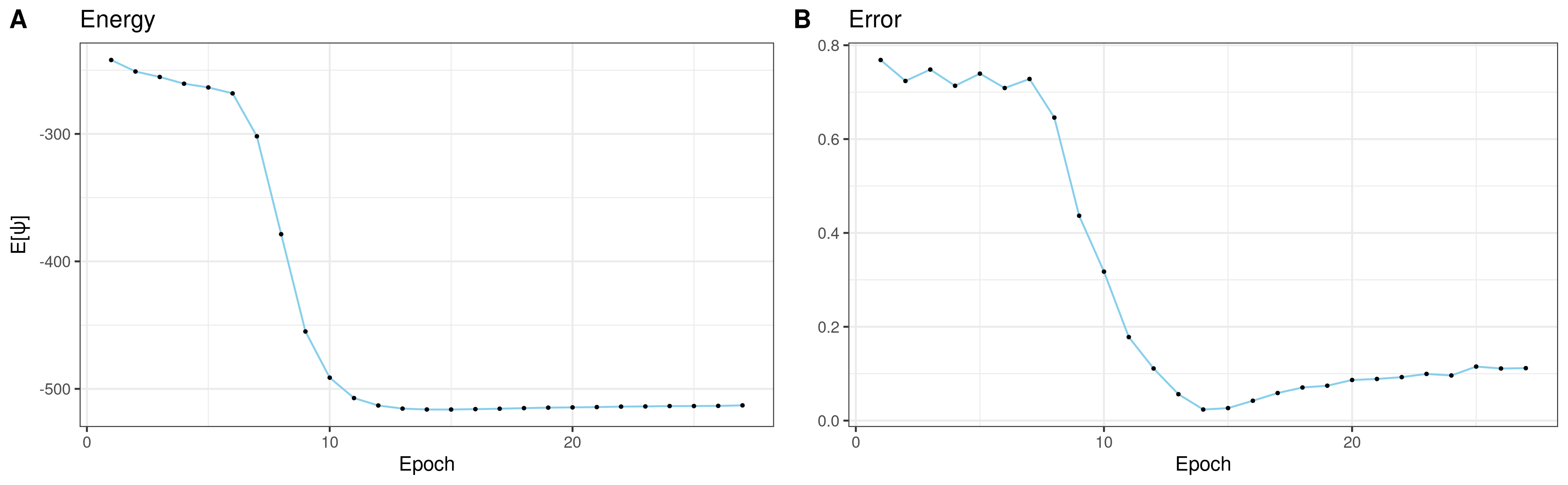
 Figure 1: Statistical expectation of
the energy and standard error of the mean for the anti-ferromagnetic
Ising chain of
Figure 1: Statistical expectation of
the energy and standard error of the mean for the anti-ferromagnetic
Ising chain of
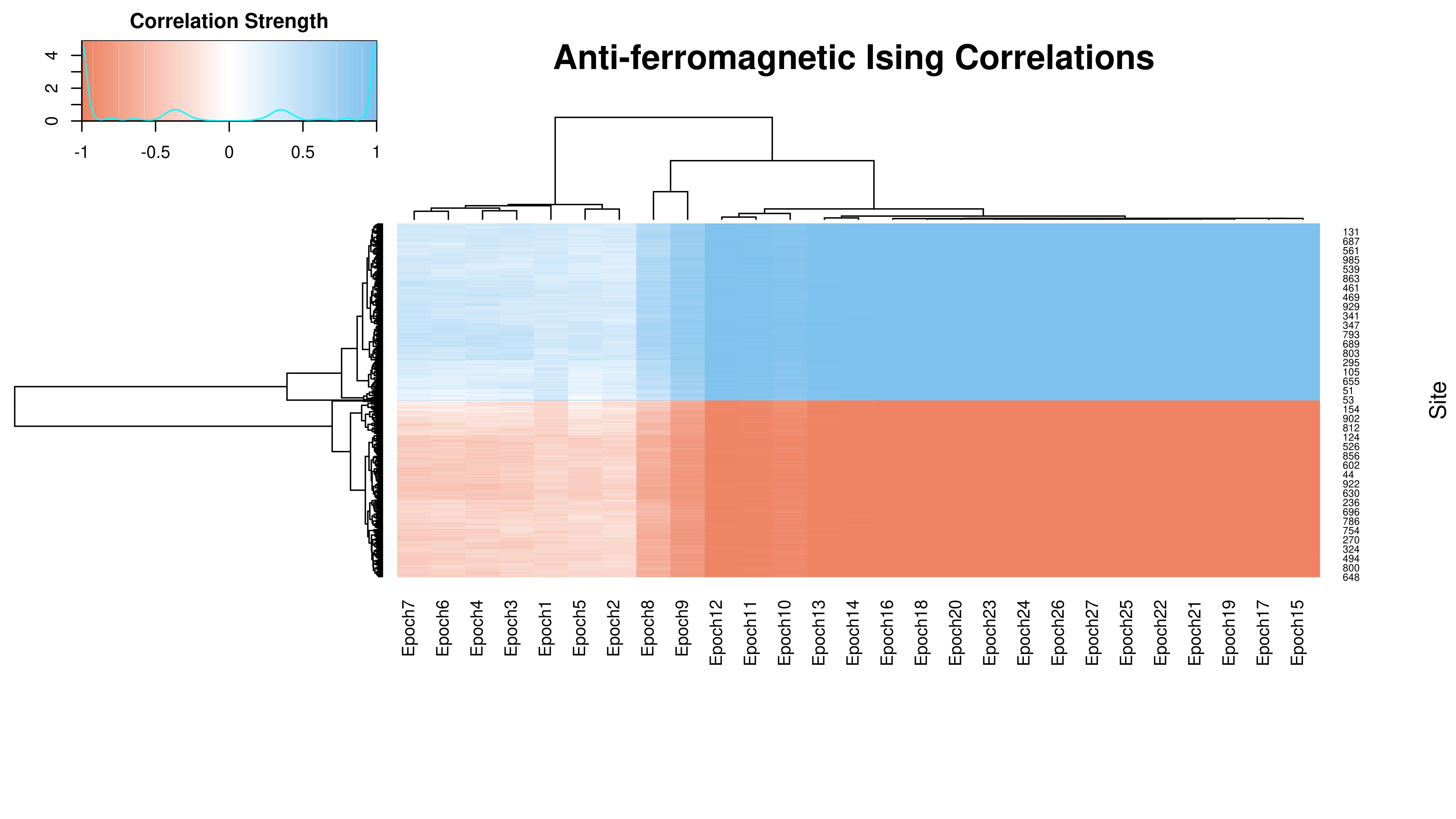 Figure 2: Correlations for
the anti-ferromagnetic Ising chain of
Figure 2: Correlations for
the anti-ferromagnetic Ising chain of
- Introduction
- Restricted Boltzmann Machines
- Neural Network Quantum States
- Transverse Field Ising Model
- Stochastic Optimization
- Derivation of Optimization Algorithm
- Fortran Implementation
- Building with fpm
Quantum mechanics emerges from classical mechanics by the relaxation of commutativity among the observables as assumed by classical probability theory. The most striking consequence of this relaxation is the insufficiency of real-valued probability distributions to encode the interference phenomena observed by experiment. In response, we generalize the notion of probability distributions from real-valued distributions over the set of possible outcomes which combine convexly, to complex-valued distributions over the set of possible outcomes which combine linearly. The complex-valued probabilities are able to encode the observed interference patterns in their relative phases. Such quantum probability distributions describe our knowledge of possible outcomes of measurements on systems which cannot be said to be in a definite state prior to measurement.
The increase in predictive power offered by quantum mechanics came with the price of computational difficulties. Unlike the classical world, whose dimensionality scales additively with the number of subsystems, the dimensionality scaling of quantum systems is multiplicative. Thus, even small systems quickly become intractable without approximation techniques. Luckily, it is rarely the case that knowledge of the full state space is required to accurately model a given system, as most information may be contained in a relatively small subspace. Many of the most successful approximation techniques of the last century, such as Born–Oppenheimer and variational techniques like Density Functional Theory, rely on this convenient notion for their success. With the rapid development of machine learning, a field which specializes in dimensionality reduction and feature extraction of very large datasets, it is natural to apply these novel techniques for dealing with the canonical large data problem of the physical sciences.
The Universal Approximation Theorems are a collection of results
concerning the ability of artificial neural networks to arbitrarily
approximate different classes of functions. In particular, the
Restricted Boltzmann Machine (RBM) is a shallow two-layer network
consisting of
Let
The RBM is a natural choice for representing wave-functions of systems
of spin
Letting
The trial state wave-functions
The variational energy functional
In this demonstration, we assume the prototypical Ising spin model for a
one-dimensional lattice of spin
Evaluating the energy functional
SUBROUTINE metropolis_hastings:
markov_chain(1) ← random_sample(n)
FOR i ∈ [2,N] DO
s ← markov_chain(i-1)
rind ← random_index(lo=1, hi=n)
s_prop ← invert_spin(config=s, at=rind)
IF r_unif(0,1) < |ψ(s_prop)/ψ(s)|^2 THEN
markov_chain(i) ← s_prop
ELSE
markov_chain(i) ← s
END IF
END FOR
RETURN markov_chain
END SUBROUTINE metropolis_hastingsIn practice, we allow for a thermalization period, or "burn-in" period,
during which the sampling process moves the initial random sample into
the stationary distribution before we can begin recording samples. As we
can see, the acceptance probabilities in the Metropolis-Hastings
algorithm and the form of the local energy involve only ratios of the
wave-functions
The stochastic optimization algorithm is a first order optimization that
involves infinitesimal variations to the parameters
Let
Similarly, we define a path
By the time-dependent Schrödinger equation, the state
To determine the actual form of the tangent vector
It must be noted that the initialization of the parameters can have a
dramatic effect on the performance of the algorithm. The initial state
- \delta \tau \Delta H \ket{\psi(\alpha(\tau))} =
\ket{\psi(\alpha(\tau))} + \delta \tau \Delta \frac{d}{d\tau}
\ket{\psi(\alpha(\tau))}$, i.e.
$$E[\psi(\alpha(\tau + \delta\tau))] = E[\psi(\alpha(\tau))] - 2\delta\tau F^\dagger(\alpha) S^{-1}(\alpha) F(\alpha) + \mathcal{O}(\delta\tau^2)$$ where$\mathcal{O}(\delta\tau^2)$ denotes the term involving$\delta\tau^2$ . Since$\delta\tau > 0$ and$S(\alpha)$ is positive-definite, the second term will be strictly negative, such that the change in energy$E[\psi(\alpha(\tau + \delta\tau))] - E[\psi(\alpha(\tau))] < 0$ for a sufficiently small time step$\delta\tau$ .
We implement the stochastic optimization algorithm as a type-bound
procedure of a type RestrictedBoltzmannMachine:
type RestrictedBoltzmannMachine
private
integer :: v_units = 0 !! Number of visible units
integer :: h_units = 0 !! Number of hidden units
real(kind=rk), allocatable, dimension(:) :: a, p_a, r_a !! Visible biases & ADAM arrays
complex(kind=rk), allocatable, dimension(:) :: b, p_b, r_b !! Hidden biases & ADAM arrays
complex(kind=rk), allocatable, dimension(:,:) :: w, p_w, r_w !! Weights & ADAM arrays
character(len=1) :: alignment = 'N' !! For tracking spin alignment
logical :: initialized = .false. !! Initialization status
contains
private
procedure, pass(self), public :: stochastic_optimization !! Public training routine
procedure, pass(self) :: init !! Initialization routine
procedure, pass(self) :: sample_distribution !! MCMC routine for sampling p(s)
procedure, pass(self) :: prob_ratio !! Probability ratio p(s_2)/p(s_1)
procedure, pass(self) :: ising_energy !! Ising local energy
procedure, pass(self) :: propagate !! Routine for updating weights and biases
end type RestrictedBoltzmannMachineIn practice, we define the visible layer biases a as type real due
to the fact that the logarithmic derivatives a, b, and w, which we use to
supplement the stochastic optimization algorithm with ADAM (Adaptive
Moment Estimation) for the purpose of numerical stability and for
smoothing the learning process for less well-behaved energy functionals.
The following is a dependency tree for the type-bound procedures:
RestrictedBoltzmannMachine
|---stochastic_optimization
| |---init
| |---sample_distribution
| | |---prob_ratio
| | |---ising_energy
| |---propagate
The stochastic_optimization routine takes advantage of the coarray
features of Fortran 2008 and, in particular, the collective subroutine
extensions of Fortran 2018, allowing for many images of the program to
run concurrently with collective communication. This allows us to
average the weights across images in each epoch of learning, which
dramatically improves stability and time to convergence in a stochastic
framework.
From a main program, we simply need to initialize the random number
generator, instantiate a RestrictedBoltzmannMachine, and call the
stochastic_optimization routine with the desired Ising model
parameters:
call random_init(repeatable=.false., image_distinct=.true.)
psi = RestrictedBoltzmannMachine(v_units, h_units)
call psi%stochastic_optimization( ising_params=[J, B] )The output data consists of energies and spin correlations, which will
be written to separate csv files in the /data folder upon successful
execution.
Note: with init, the biases are initialized to zero prior to training,
and the weights have both real and imaginary parts initialized with
samples from a standard Gaussian distribution using a routine adapted
from
ROOT.
The only dependency of this project is the Intel MKL distribution of LAPACK. With a system installation of Intel oneAPI Base and HPC toolkits (including MKL), the project can be built and run on Windows 10/11 and Linux with fpm from the project root using a single command, assuming the shell environment has sourced the oneAPI environment variables beforehand.
To target an
fpm run --compiler ifort --flag "/Qcoarray /Qcoarray-num-images:n /Qopenmp /Qopenmp-simd" --link-flag "mkl_lapack95_lp64.lib mkl_intel_lp64.lib mkl_intel_thread.lib mkl_core.lib libiomp5md.lib"and on Linux using the command
fpm run --compiler ifort --flag "-coarray -coarray-num-images=n -qopenmp -qopenmp-simd" --link-flag "-Wl,--start-group ${MKLROOT}/lib/intel64/libmkl_lapack95_lp64.a ${MKLROOT}/lib/intel64/libmkl_intel_lp64.a ${MKLROOT}/lib/intel64/libmkl_intel_thread.a ${MKLROOT}/lib/intel64/libmkl_core.a -liomp5 -lpthread -lm -ldl"with equivalent features.
Here, n is the number of images to execute, which generally should
equal the number of CPU cores available. We then enable the generation
of multi-threaded code with OpenMP and SIMD compilation. Finally, the
link flag specifies the MKL and OpenMP runtime libraries for static
linking, provided by the Intel Link Line
Advisor.
To target an
fpm run --compiler ifx --flag "/Qcoarray /Qcoarray-num-images:n /Qiopenmp /Qopenmp-targets:spir64 /Qopenmp-target-do-concurrent" --link-flag "mkl_lapack95_lp64.lib mkl_intel_lp64.lib mkl_intel_thread.lib mkl_core.lib libiomp5md.lib OpenCL.lib"and on Linux using the command
fpm run --compiler ifx --flag "-coarray -coarray-num-images=n -fiopenmp -fopenmp-targets=spir64 -fopenmp-target-do-concurrent" --link-flag "-Wl,--start-group ${MKLROOT}/lib/intel64/libmkl_lapack95_lp64.a ${MKLROOT}/lib/intel64/libmkl_intel_lp64.a ${MKLROOT}/lib/intel64/libmkl_intel_thread.a ${MKLROOT}/lib/intel64/libmkl_core.a -liomp5 -lOpenCL -lpthread -lm -ldl"with equivalent features.