Recursion is a technique in which a function calls itself, breaking problems down into simpler instances of the same problem. It's fundamental in solving problems like tree traversals and combinatorial tasks. In coding interviews, recursion questions evaluate a candidate's ability to think in terms of self-referential logic and their grasp on base cases and recursive steps.

Check out our carefully selected list of basic and advanced Recursion questions and answers to be well-prepared for your tech interviews in 2024.

👉🏼 You can also find all answers here: Devinterview.io - Recursion

Let's look into some examples and see how they utilize the core concepts of recursion.

In binary tree traversal, nodes are visited recursively, exploring the left and right subtrees in various orders.

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def in_order_traversal(node):
    if node is not None:
        in_order_traversal(node.left)
        print(node.value)
        in_order_traversal(node.right)

A palindrome is a word, phrase, number, or other sequence of characters that reads the same forward and backward. To determine a palindrome, the outer characters of a word are compared. If they match, the inner substring is checked recursively.

def is_palindrome(word):
    if len(word) <= 1:
        return True
    if word[0] == word[-1]:
        return is_palindrome(word[1:-1])
    return False

The factorial of a number is calculated using a base and recursive case. $0! = 1$ and $n! = n \times (n-1)!$.

def factorial(n):
    if n == 0:
        return 1
    return n * factorial(n-1)

A folder hierarchy in a file system can be traversed recursively, exploring the contents of each directory.

import os

def folder_contents(path):
    for item in os.listdir(path):
        item_path = os.path.join(path, item)
        if os.path.isfile(item_path):
            print(f"Found a file: {item_path}")
        elif os.path.isdir(item_path):
            print(f"Entering folder: {item_path}")
            folder_contents(item_path)

The Towers of Hanoi is a mathematical puzzle that involves three pegs and a set of disks of different sizes, which can be moved from one peg to another following a set of rules. It's often used as an example in computer science textbooks to illustrate how recursion can be used to solve problems.

def tower_of_hanoi(n, source, target, auxiliary):
    if n == 1:
        print(f"Move disk 1 from {source} to {target}")
        return
    tower_of_hanoi(n-1, source, auxiliary, target)
    print(f"Move disk {n} from {source} to {target}")
    tower_of_hanoi(n-1, auxiliary, target, source)

This sorting algorithm follows the divide-and-conquer paradigm, using recursion to split and then merge lists.

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left_half = arr[:mid]
    right_half = arr[mid:]
    left_half = merge_sort(left_half)
    right_half = merge_sort(right_half)
    return merge(left_half, right_half)

The Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involving recursive structures. The recursive formula for the $n$-th Catalan number is

$$ C_n = \sum_{i=0}^{n-1} C_i \cdot C_{n-1-i} $$

where the base case is $C_0 = 1$.

Backtracking often employs recursion to explore the vast space of possible solutions. However, not all recursive algorithms involve backtracking.

Think of recursion as the mechanism that enables a function to call itself, and backtracking as a strategy where you make a choice and explore the possibilities.

• Recursion: Utilizes a divide-and-conquer approach, breaking the main problem into smaller, self-similar subproblems. Recursive calls work towards solving these subproblems, relying on defined base cases for termination.

• Backtracking: Operates as an advanced form of recursion by building solutions incrementally. When a partial solution is deemed unsuitable, it "backtracks" to modify previous choices, ensuring an efficient traversal through the solution space.

• Tree Traversals: Visiting all nodes in a tree, like in binary search trees.
• Divide and Conquer Algorithms: Such as merge sort or quick sort.
• Dynamic Programming: Solving problems like the coin change problem by breaking them down into smaller subproblems.

• Puzzle Solvers: Solving games like Sudoku or crossword puzzles.
• Combinatorial Problems: Generating all permutations or combinations of a set.
• Decision-making Problems: Such as the knapsack problem, where decisions are made on whether to include items.

Dynamic Programming (DP), Recursion, and Memoization are techniques for solving problems that can be divided into smaller, overlapping sub-problems. While they share this commonality, they each offer unique advantages and limitations.

1. Efficiency: DP typically leads to polynomial-time algorithms, whereas Recursion and Memoization can result in higher time complexities.

2. Problem-Solving Direction: DP builds solutions from the ground up, focusing on smaller sub-problems first. In contrast, Recursion and Memoization usually adopt a top-down approach.

3. Implementation Style: DP and Memoization can be implemented either iteratively or recursively, while Recursion is, by definition, a recursive technique.

4. Sub-Problem Coverage: DP aims to solve all relevant sub-problems, whereas Memoization and Recursion solve sub-problems on an as-needed basis.

5. Memory Use: DP often requires less memory than Memoization, as it doesn't store every state reached through recursive calls.

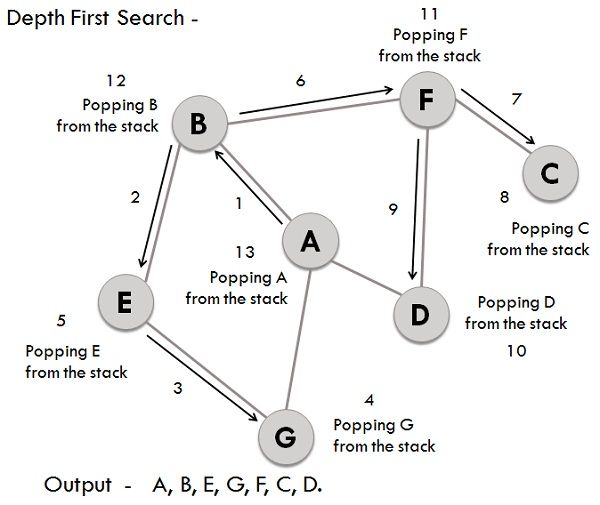
Depth-First Search (DFS) is a graph traversal algorithm that's simpler and often faster than its breadth-first counterpart (BFS). While it might not explore all vertices, DFS is still fundamental to numerous graph algorithms.

1. Initialize: Select a starting vertex, mark it as visited, and put it on a stack.
2. Loop: Until the stack is empty, do the following:
   • Remove the top vertex from the stack.
   • Explore its unvisited neighbors and add them to the stack.
3. Finish: When the stack is empty, the algorithm ends, and all reachable vertices are visited.

Here is the Python code:

def dfs(graph, start):
    visited = set()
    stack = [start]
    
    while stack:
        vertex = stack.pop()
        if vertex not in visited:
            visited.add(vertex)
            stack.extend(neighbor for neighbor in graph[vertex] if neighbor not in visited)
    
    return visited

# Example graph
graph = {
    'A': {'B', 'G'},
    'B': {'A', 'E', 'F'},
    'G': {'A'},
    'E': {'B', 'G'},
    'F': {'B', 'C', 'D'},
    'C': {'F'},
    'D': {'F'}
}

print(dfs(graph, 'A'))  # Output: {'A', 'B', 'C', 'D', 'E', 'F', 'G'}

👉🏼 Check out all 11 answers here: Devinterview.io - Recursion

👉🏼 Check out all 11 answers here: Devinterview.io - Recursion

👉🏼 Check out all 11 answers here: Devinterview.io - Recursion

👉🏼 Check out all 11 answers here: Devinterview.io - Recursion

👉🏼 Check out all 11 answers here: Devinterview.io - Recursion

👉🏼 Check out all 11 answers here: Devinterview.io - Recursion

👉🏼 Check out all 11 answers here: Devinterview.io - Recursion