
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
# 647. 回文子串
[力扣题目链接](https://leetcode.cn/problems/palindromic-substrings/)
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
* 输入:"abc"
* 输出:3
* 解释:三个回文子串: "a", "b", "c"
示例 2:
* 输入:"aaa"
* 输出:6
* 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示:输入的字符串长度不会超过 1000 。
## 暴力解法
两层for循环,遍历区间起始位置和终止位置,然后还需要一层遍历判断这个区间是不是回文。所以时间复杂度:O(n^3)
## 动态规划
动规五部曲:
1. 确定dp数组(dp table)以及下标的含义
如果大家做了很多这种子序列相关的题目,在定义dp数组的时候 很自然就会想题目求什么,我们就如何定义dp数组。
绝大多数题目确实是这样,不过本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。
dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
所以我们要看回文串的性质。 如图:
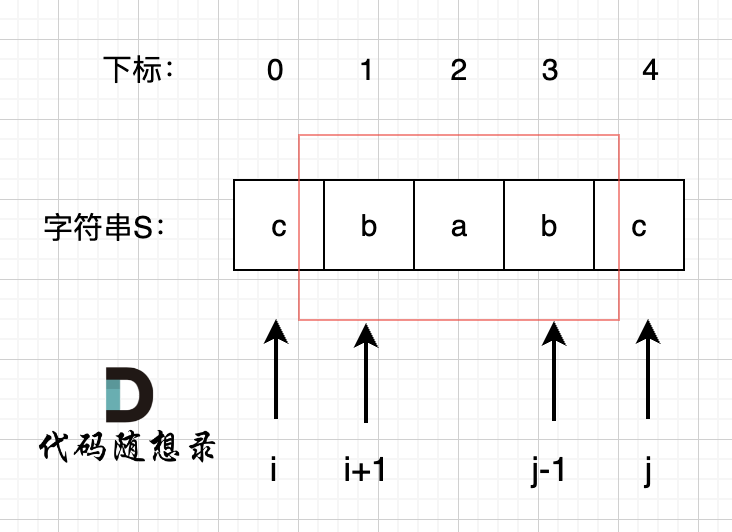
我们在判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
那么此时我们是不是能找到一种递归关系,也就是判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文。
所以为了明确这种递归关系,我们的dp数组是要定义成一位二维dp数组。
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
2. 确定递推公式
在确定递推公式时,就要分析如下几种情况。
整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
* 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
* 情况二:下标i 与 j相差为1,例如aa,也是回文子串
* 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
以上三种情况分析完了,那么递归公式如下:
```CPP
if (s[i] == s[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // 情况三
result++;
dp[i][j] = true;
}
}
```
result就是统计回文子串的数量。
注意这里我没有列出当s[i]与s[j]不相等的时候,因为在下面dp[i][j]初始化的时候,就初始为false。
3. dp数组如何初始化
dp[i][j]可以初始化为true么? 当然不行,怎能刚开始就全都匹配上了。
所以dp[i][j]初始化为false。
4. 确定遍历顺序
遍历顺序可有有点讲究了。
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
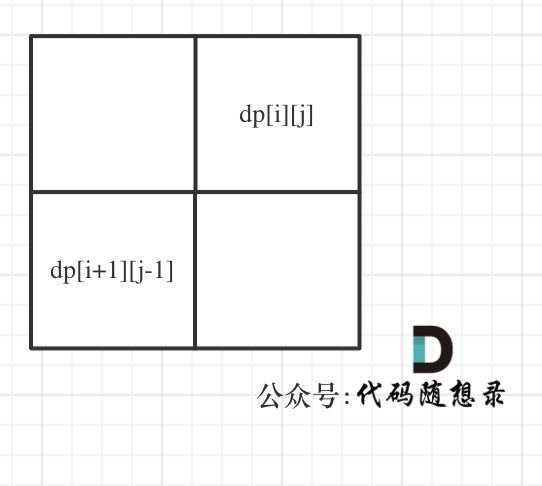
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
**所以一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的**。
有的代码实现是优先遍历列,然后遍历行,其实也是一个道理,都是为了保证dp[i + 1][j - 1]都是经过计算的。
代码如下:
```CPP
for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // 情况三
result++;
dp[i][j] = true;
}
}
}
}
```
5. 举例推导dp数组
举例,输入:"aaa",dp[i][j]状态如下:

图中有6个true,所以就是有6个回文子串。
**注意因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分**。
以上分析完毕,C++代码如下:
```CPP
class Solution {
public:
int countSubstrings(string s) {
vector> dp(s.size(), vector(s.size(), false));
int result = 0;
for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // 情况三
result++;
dp[i][j] = true;
}
}
}
}
return result;
}
};
```
以上代码是为了凸显情况一二三,当然是可以简洁一下的,如下:
```CPP
class Solution {
public:
int countSubstrings(string s) {
vector> dp(s.size(), vector(s.size(), false));
int result = 0;
for (int i = s.size() - 1; i >= 0; i--) {
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {
result++;
dp[i][j] = true;
}
}
}
return result;
}
};
```
* 时间复杂度:O(n^2)
* 空间复杂度:O(n^2)
## 双指针法
动态规划的空间复杂度是偏高的,我们再看一下双指针法。
首先确定回文串,就是找中心然后向两边扩散看是不是对称的就可以了。
**在遍历中心点的时候,要注意中心点有两种情况**。
一个元素可以作为中心点,两个元素也可以作为中心点。
那么有人同学问了,三个元素还可以做中心点呢。其实三个元素就可以由一个元素左右添加元素得到,四个元素则可以由两个元素左右添加元素得到。
所以我们在计算的时候,要注意一个元素为中心点和两个元素为中心点的情况。
**这两种情况可以放在一起计算,但分别计算思路更清晰,我倾向于分别计算**,代码如下:
```CPP
class Solution {
public:
int countSubstrings(string s) {
int result = 0;
for (int i = 0; i < s.size(); i++) {
result += extend(s, i, i, s.size()); // 以i为中心
result += extend(s, i, i + 1, s.size()); // 以i和i+1为中心
}
return result;
}
int extend(const string& s, int i, int j, int n) {
int res = 0;
while (i >= 0 && j < n && s[i] == s[j]) {
i--;
j++;
res++;
}
return res;
}
};
```
* 时间复杂度:O(n^2)
* 空间复杂度:O(1)
## 其他语言版本
Java:
动态规划:
```java
class Solution {
public int countSubstrings(String s) {
int len, ans = 0;
if (s == null || (len = s.length()) < 1) return 0;
//dp[i][j]:s字符串下标i到下标j的字串是否是一个回文串,即s[i, j]
boolean[][] dp = new boolean[len][len];
for (int j = 0; j < len; j++) {
for (int i = 0; i <= j; i++) {
//当两端字母一样时,才可以两端收缩进一步判断
if (s.charAt(i) == s.charAt(j)) {
//i++,j--,即两端收缩之后i,j指针指向同一个字符或者i超过j了,必然是一个回文串
if (j - i < 3) {
dp[i][j] = true;
} else {
//否则通过收缩之后的字串判断
dp[i][j] = dp[i + 1][j - 1];
}
} else {//两端字符不一样,不是回文串
dp[i][j] = false;
}
}
}
//遍历每一个字串,统计回文串个数
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
if (dp[i][j]) ans++;
}
}
return ans;
}
}
```
中心扩散法:
```java
class Solution {
public int countSubstrings(String s) {
int len, ans = 0;
if (s == null || (len = s.length()) < 1) return 0;
//总共有2 * len - 1个中心点
for (int i = 0; i < 2 * len - 1; i++) {
//通过遍历每个回文中心,向两边扩散,并判断是否回文字串
//有两种情况,left == right,right = left + 1,这两种回文中心是不一样的
int left = i / 2, right = left + i % 2;
while (left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {
//如果当前是一个回文串,则记录数量
ans++;
left--;
right++;
}
}
return ans;
}
}
```
Python:
> 动态规划:
```python
class Solution:
def countSubstrings(self, s: str) -> int:
dp = [[False] * len(s) for _ in range(len(s))]
result = 0
for i in range(len(s)-1, -1, -1): #注意遍历顺序
for j in range(i, len(s)):
if s[i] == s[j]:
if j - i <= 1: #情况一 和 情况二
result += 1
dp[i][j] = True
elif dp[i+1][j-1]: #情况三
result += 1
dp[i][j] = True
return result
```
> 动态规划:简洁版
```python
class Solution:
def countSubstrings(self, s: str) -> int:
dp = [[False] * len(s) for _ in range(len(s))]
result = 0
for i in range(len(s)-1, -1, -1): #注意遍历顺序
for j in range(i, len(s)):
if s[i] == s[j] and (j - i <= 1 or dp[i+1][j-1]):
result += 1
dp[i][j] = True
return result
```
> 双指针法:
```python
class Solution:
def countSubstrings(self, s: str) -> int:
result = 0
for i in range(len(s)):
result += self.extend(s, i, i, len(s)) #以i为中心
result += self.extend(s, i, i+1, len(s)) #以i和i+1为中心
return result
def extend(self, s, i, j, n):
res = 0
while i >= 0 and j < n and s[i] == s[j]:
i -= 1
j += 1
res += 1
return res
```
Go:
```Go
func countSubstrings(s string) int {
res:=0
dp:=make([][]bool,len(s))
for i:=0;i=0;i--{
for j:=i;j 动态规划
```javascript
const countSubstrings = (s) => {
const strLen = s.length;
let numOfPalindromicStr = 0;
let dp = Array.from(Array(strLen), () => Array(strLen).fill(false));
for(let j = 0; j < strLen; j++) {
for(let i = 0; i <= j; i++) {
if(s[i] === s[j]) {
if((j - i) < 2) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i+1][j-1];
}
numOfPalindromicStr += dp[i][j] ? 1 : 0;
}
}
}
return numOfPalindromicStr;
}
```
> 双指针法:
```javascript
const countSubstrings = (s) => {
const strLen = s.length;
let numOfPalindromicStr = 0;
for(let i = 0; i < 2 * strLen - 1; i++) {
let left = Math.floor(i/2);
let right = left + i % 2;
while(left >= 0 && right < strLen && s[left] === s[right]){
numOfPalindromicStr++;
left--;
right++;
}
}
return numOfPalindromicStr;
}
```
TypeScript:
> 动态规划:
```typescript
function countSubstrings(s: string): number {
/**
dp[i][j]: [i,j]区间内的字符串是否为回文(左闭右闭)
*/
const length: number = s.length;
const dp: boolean[][] = new Array(length).fill(0)
.map(_ => new Array(length).fill(false));
let resCount: number = 0;
// 自下而上,自左向右遍历
for (let i = length - 1; i >= 0; i--) {
for (let j = i; j < length; j++) {
if (
s[i] === s[j] &&
(j - i <= 1 || dp[i + 1][j - 1] === true)
) {
dp[i][j] = true;
resCount++;
}
}
}
return resCount;
};
```
> 双指针法:
```typescript
function countSubstrings(s: string): number {
const length: number = s.length;
let resCount: number = 0;
for (let i = 0; i < length; i++) {
resCount += expandRange(s, i, i);
resCount += expandRange(s, i, i + 1);
}
return resCount;
};
function expandRange(s: string, left: number, right: number): number {
let palindromeNum: number = 0;
while (
left >= 0 && right < s.length &&
s[left] === s[right]
) {
palindromeNum++;
left--;
right++;
}
return palindromeNum;
}
```

